
أي شخص فكر في أي وقت مضىلكي تصبح متخصصًا في تكنولوجيا المعلومات أو مسؤول النظام ، وببساطة لتوصيل المصير بتكنولوجيا الكمبيوتر ، من الضروري للغاية معرفة كيفية تمثيل الأرقام في ذاكرة الكمبيوتر. في الواقع ، هذا هو المكان الذي تستند إليه لغات البرمجة منخفضة المستوى مثل Assembler. لذلك ، سننظر اليوم في تمثيل الأرقام في الكمبيوتر ووضعها في خلايا الذاكرة.

إذا كنت تقرأ هذه المقالة ، فعلى الأرجحتعرف بالفعل عن ذلك ، ولكن يستحق التكرار. يتم تخزين جميع البيانات في جهاز الكمبيوتر الشخصي في نظام رقم ثنائي. وهذا يعني أنه يجب تمثيل أي رقم بالشكل المناسب ، أي يتكون من أصفار وأرقام.
لترجمة الأرقام العشرية المعتادة إلى نموذج يمكن فهمه على جهاز الكمبيوتر ، تحتاج إلى استخدام الخوارزمية الموضحة أدناه. هناك أيضا حاسبات متخصصة.
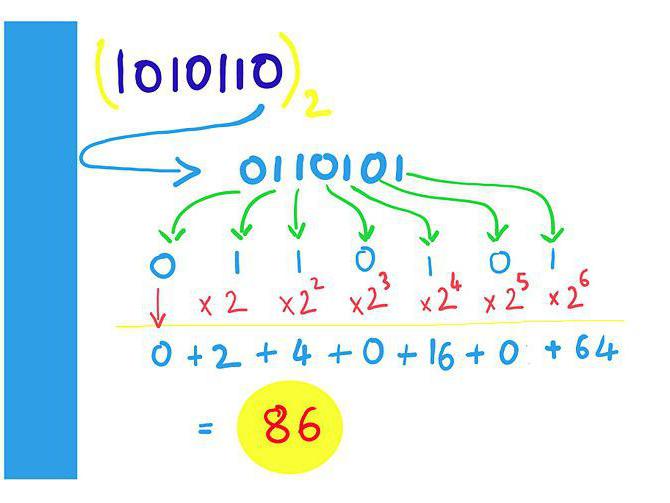
لذا ، من أجل تحويل الرقم إلى ثنائينظام الأرقام ، تحتاج إلى أخذ القيمة التي حددناها وتقسيمها على 2. بعد ذلك ، نحصل على النتيجة والباقي (0 أو 1). قسّم النتيجة مرة أخرى 2 وتذكر الباقي. يجب تكرار هذا الإجراء حتى في النهاية هناك أيضًا 0 أو 1. ثم نقوم بتدوين القيمة النهائية والمخلفات بالترتيب العكسي ، كما تلقيناها.
هذه هي الطريقة التي يحدث بها تمثيل الأرقام في جهاز الكمبيوتر. يتم كتابة أي رقم في شكل ثنائي ، ثم يشغل خلية ذاكرة.

كما يجب أن تعرف بالفعل ، الحد الأدنىوحدة المعلومات هي 1 بت. كما اكتشفنا بالفعل ، يتم تمثيل الأرقام في جهاز الكمبيوتر بتنسيق ثنائي. وبالتالي ، سيتم شغل كل جزء من الذاكرة بقيمة واحدة - 1 أو 0.
تستخدم الخلايا لتخزين أعداد كبيرة.تحتوي كل وحدة على ما يصل إلى 8 بتات من المعلومات. لذلك ، يمكننا أن نستنتج أن الحد الأدنى للقيمة في كل مقطع ذاكرة يمكن أن يكون بايت واحد أو أن يكون رقمًا ثنائيًا مكونًا من ثمانية أرقام.
أخيرًا ، وصلنا إلى وضع البيانات مباشرة على الكمبيوتر. كما ذكرنا من قبل ، يقوم المعالج أولاً بتحويل المعلومات إلى تنسيق ثنائي ، ثم فقط يضعها في الذاكرة.
نبدأ مع أبسط خيار ، وهوهو تمثيل الأعداد الصحيحة في الكمبيوتر. تأخذ ذاكرة الكمبيوتر عددًا صغيرًا للغاية من الخلايا لهذه العملية - واحدة فقط. وبالتالي ، يمكن أن يكون الحد الأقصى في فتحة واحدة قيمًا من 0 إلى 11111111. دعنا نترجم العدد الأقصى إلى شكل مألوف للكتابة.
س = 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 1 × 28 - 1 = 255.
الآن نرى أنه في خلية ذاكرة واحدة يمكنتتراوح من 0 إلى 255. ومع ذلك ، فإن هذا ينطبق حصريًا على الأعداد الصحيحة غير السلبية. إذا كان الكمبيوتر بحاجة إلى كتابة قيمة سالبة ، فسيسير كل شيء بشكل مختلف قليلاً.

الآن دعونا نرى كيف ستسير الامورتمثيل الأرقام على الكمبيوتر إذا كانت سلبية. لوضع قيمة أقل من الصفر ، يتم تخصيص خليتي ذاكرة أو 16 بت من المعلومات. في هذه الحالة ، تدخل 15 تحت الرقم نفسه ، ويتم إعطاء البت الأول (أقصى اليسار) تحت العلامة المقابلة.
إذا كان الرقم سالبًا ، فسيتم كتابة "1" ، وإذا كان موجبًا ، عندئذٍ يتم كتابة "0". لسهولة الحفظ ، يمكننا رسم القياس: إذا كان هناك علامة ، ثم ضع 1 ، إذا لم يكن كذلك ، فلا شيء (0).
يتم تخصيص 15 بت المتبقية من المعلومات إلى الرقم.على غرار الحالة السابقة ، يمكنك وضع خمسة عشر وحدة بحد أقصى فيها. تجدر الإشارة إلى أن كتابة أرقام سلبية وإيجابية تختلف اختلافًا كبيرًا عن بعضها البعض.
من أجل وضعه في موقعين للذاكرةقيمة أكبر من الصفر أو تساويها ، يتم استخدام ما يسمى بالرمز المباشر. يتم تنفيذ هذه العملية بنفس الطريقة التي تم وصفها ، والحد الأقصى هو A = 32766 ، إذا كنت تستخدم نظام الأرقام العشرية. ما عليك سوى ملاحظة أنه في هذه الحالة ، يشير الرقم "0" إلى "إيجابي".
تمثيل الأعداد الصحيحة في ذاكرة الكمبيوتر ليس كذلكهي مهمة صعبة. على الرغم من أنها أكثر تعقيدًا عندما يتعلق الأمر بقيمة سلبية. لكتابة رقم أقل من الصفر ، يتم استخدام رمز إضافي.
للحصول عليه ، تقوم الآلة بعدد من العمليات المساعدة.
نعطي مثال واضح.لنفترض أن لدينا الرقم X = - 131. أولاً نحصل على الوحدة النمطية | X | = 131. ثم نترجمها إلى نظام ثنائي ونكتبها في 16 خلية. نحصل على X = 0000000010000011. بعد قلب X = 1111111101111100. أضف "1" إليه واحصل على رمز الإرجاع X = 1111111101111101. للكتابة على خلية ذاكرة 16 بت ، الحد الأدنى هو X = - (215) = - 32767.
كما ترون ، تمثيل الأعداد الحقيقية فيالكمبيوتر ليس بهذه الصعوبة. ومع ذلك ، قد لا يكون النطاق المعتبر كافياً لمعظم العمليات. لذلك ، من أجل استيعاب أعداد كبيرة ، يقوم الكمبيوتر بتخصيص 4 خلايا أو 32 بت من الذاكرة.
لا تختلف عملية التسجيل على الإطلاق عما سبق. لذلك نقدم فقط مجموعة من الأرقام التي يمكن تخزينها في هذا النوع.
Xماكس= 2،147،483،647.
Xدقيقة= - 2،147،483،648.

في معظم الحالات ، تكون هذه القيم كافية لتسجيل وإجراء عمليات البيانات.
تمثيل الأعداد الحقيقية في الكمبيوترمزاياه وعيوبه. من ناحية ، تسهل هذه التقنية إجراء العمليات بين القيم الصحيحة ، مما يسرع المعالج بشكل كبير. من ناحية أخرى ، هذا النطاق لا يكفي لحل معظم مشاكل الاقتصاد والفيزياء والحساب وغيرها من العلوم. لذلك ، سننظر الآن في المنهجية التالية للكميات الفائقة.
هذا هو آخر شيء تحتاج إلى معرفتهتمثيل الأرقام في الكمبيوتر. نظرًا لأن مشكلة تحديد موضع الفاصلة فيها تنشأ عند كتابة الكسور ، يتم استخدام نموذج أسي لوضع هذه الأرقام في الكمبيوتر.
يمكن تمثيل أي رقم بالصيغة التالية X = m * pن. حيث m هي الجزء العشري من الرقم ، p هي أساس نظام الأرقام ، و n هو ترتيب الرقم.
لتوحيد تدوين أرقام الفاصلة العائمة ، يتم استخدام الشرط التالي ، والذي بموجبه يجب أن تكون وحدة العشري أكبر من أو تساوي 1 / n وأقل من 1.
دعونا نعطي الرقم 666.66. نأتي بها إلى شكل أسي. اتضح X = 0.66666 * 103. P = 10 و n = 3.
عادة ما يتم تخصيص 4 أو 8 بايت (32 أو 64 بت) لتخزين قيم النقطة العائمة. في الحالة الأولى ، يسمى هذا عدد الدقة العادية ، وفي الثانية - الدقة المزدوجة.
من 4 بايت مخصصة لتخزين الأرقام ، 1 (8البتات) للحصول على بيانات عن الطلب وعلامته ، و 3 بايت (24 بت) تذهب إلى تخزين الجزء العشري وعلامته وفقًا لنفس المبادئ مثل القيم الصحيحة. بمعرفة هذا ، يمكننا إجراء حسابات بسيطة.
القيمة القصوى n = 11111112 = 12710. وبناءً عليه ، يمكننا الحصول على أقصى حجم لرقم يمكن تخزينه في ذاكرة الكمبيوتر. س = 2127. الآن يمكننا حساب أقصى عزم ممكن. ستكون مساوية لـ 223 - 1 ≥ 223 = 2(10 × 2.3) ≥ 10002,3 = 10(3 × 2،3) ≥ 107. نتيجة لذلك ، حصلنا على قيمة تقريبية.
إذا قمنا الآن بدمج كلا الحسابين ، نحصل على قيمة يمكن تسجيلها بدون فقدان في 4 بايت من الذاكرة. ستكون مساوية لـ X = 1،701411 * 1038. تم التخلص من الأرقام المتبقية ، حيث إن هذه الدقة هي التي تسمح بطريقة التسجيل هذه.

حيث تم جدولة جميع الحسابات وموضح في الفقرة السابقة ، هنا سنخبرك بإيجاز شديد. للأرقام ذات الدقة المزدوجة ، عادة ما يتم تخصيص 11 رقمًا للأمر وعلامته ، بالإضافة إلى 53 رقمًا للعشري.
P = 11111111112 = 102310.
م = 252 -1 = 2(10 * 5.2) = 10005.2 = 1015.6. نقرّب ونحصل على أقصى عدد X = 21023 دقيقة ل "م".
نأمل أن تكون المعلومات الخاصة بتمثيل الأعداد الصحيحة والأرقام الحقيقية على جهاز الكمبيوتر التي قدمناها مفيدة لك في التدريب وستكون على الأقل أكثر وضوحا مما هو مكتوب عادة في الكتب المدرسية.


























