
قليل من الناس يفكر في التقنيات والصيغ التي نستخدمها لحساب الأرقام البسيطة أو المعقدة قد تشكلت على مدى قرون عديدة ، وفي أجزاء مختلفة من العالم. كانت المهارات الرياضية الحديثة ، والتي حتى المبتدئ الأول على دراية بها ، غامرة في السابق لأذكى الناس. قدم نظام الأرقام المصري مساهمة كبيرة في تطوير هذه الصناعة ، وبعض العناصر التي ما زلنا نستخدمها في شكلها الأصلي.
المؤرخون الموثوقون يعرفون ذلك في أيحضارة قديمة وضعت أساسا الكتابة ، والقيم العددية دائما وقفت في المركز الثاني. لهذا السبب ، في رياضيات آلاف السنين الماضية هناك العديد من الأخطاء ، والخبراء الحديث في بعض الأحيان لغز في مثل هذه الألغاز. نظام الأرقام المصري ، الذي ، بالمناسبة ، كان أيضًا غير موضعي ، لم يكن استثناءً. هذا يعني أن موضع رقم واحد في سجل الأرقام لا يغير القيمة الإجمالية. كمثال ، خذ بعين الاعتبار القيمة 15 ، حيث 1 في المقام الأول ، و 5 في الثانية. إذا قمنا بتبديل هذه الأرقام ، فسوف نحصل على عدد أكبر بكثير. لكن نظام الأرقام المصري القديم لم يشر إلى مثل هذه التغييرات. حتى في العدد الأكثر أهمية ، تم تسجيل جميع مكوناته بترتيب عشوائي.

لاحظ فقط أن السكان المعاصرين لهذا البلد الحار يستخدمون نفس الأرقام العربية التي نستخدمها ، وكتابتها وفقًا للترتيب الدقيق ومن اليسار إلى اليمين.
استخدم المصريون الهيروغليفية لكتابة الأرقامولم يكن هناك الكثير منهم. استنساخها وفقا لقاعدة معينة ، كان من الممكن الحصول على عدد من أي حجم ، ولكن هذا يتطلب الكثير من ورق البردي. في المرحلة الأولى من وجوده ، احتوى نظام الأرقام الهيروغليفية المصرية على الأرقام 1 و 10 و 100 و 1000 و 10000. في وقت لاحق ، ظهرت أعداد أكثر أهمية ومضاعفات 10. إذا كنت بحاجة إلى تدوين أحد المؤشرات أعلاه ، فقد استخدمنا الهيروغليفية التالية:

لكتابة رقم لا يتعدى عشرة ، تم استخدام هذه التقنية البسيطة:

نتيجة المثال أعلاه ، نحننرى أنه في المقام الأول لدينا 6 مئة معيّنة ، تليهم اثنتان وعشرون وحدة في النهاية. وبالمثل ، يتم تسجيل أي أرقام أخرى يمكن من خلالها استخدام آلاف وعشرات الآلاف. ومع ذلك ، يتم كتابة هذا المثال من اليسار إلى اليمين ، بحيث يمكن للقارئ الحديث فهمه بشكل صحيح ، فقط في الواقع لم يكن نظام الأرقام المصري دقيقًا. يمكن كتابة نفس القيمة من اليمين إلى اليسار ، لمعرفة أين البداية والمكان ، حيث يتم حساب النهاية ، بناءً على الشكل ذي القيمة الأعلى. ستكون هناك حاجة أيضًا إلى نقطة مرجعية مماثلة إذا كانت الأرقام مكتوبة بأعداد كبيرة متناثرة (لأن النظام غير موضعي).
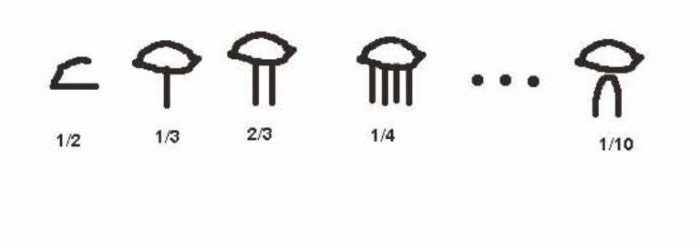
كان المصريون يتقنون الرياضيات قبل العديد من الآخرين.لهذا السبب ، في مرحلة ما ، لم تكن الأرقام وحدها كافية ، وتم إدخال الكسور تدريجياً. نظرًا لأن نظام الأرقام المصري القديم يُعتبر الهيروغليفية ، فقد استخدمت الرموز أيضًا لتسجيل البسط والقواسم. بالنسبة لـ ½ كان هناك علامة خاصة وغير متغيرة ، وتم تشكيل جميع المؤشرات الأخرى بنفس الطريقة التي تم استخدامها للأعداد الكبيرة. لطالما أظهر البسط رمزًا يقلد شكل العين البشرية ، وقد تمت الإشارة إلى الرقم بالفعل في المقام.
إذا كانت هناك أرقام ، يتم إضافتها وطرحها ،اضرب و اقسم. تعامل نظام الأرقام المصري مع هذه المهمة تمامًا ، على الرغم من وجود خصوصية. أسهل طريقة لإضافة وطرح. لهذا ، تمت كتابة الهيروغليفية المكونة من رقمين على التوالي ، وأخذ تغيير الأرقام بينهما في الاعتبار. من الأصعب فهم كيفية تكاثرها ، لأن هذه العملية تشبه إلى حد ما العملية الحديثة. يتكون عمودين ، أحدهما بدأ بوحدة ، والآخر بعامل ثانٍ. ثم بدأوا في مضاعفة كل من هذه الأرقام ، وكتابة نتيجة جديدة تحت الرقم السابق. عندما كان من الممكن جمع العامل المفقود من الأرقام الفردية للعمود الأول ، تم تلخيص النتائج. يمكنك فهم هذه العملية بشكل أفضل من خلال النظر إلى الطاولة. في هذه الحالة ، 7 مرات 22:

النتيجة في العمود الأول من 8 تتجاوز بالفعل 7 ، لذلك ينتهي المضاعفة عند 4. 1 + 2 + 4 = 7 ، و 22 + 44 + 88 = 154. هذه الإجابة صحيحة ، رغم أننا حصلنا عليها بطريقة غير قياسية.
تم إجراء الطرح والقسمة بالترتيب العكسي للجمع والضرب.
تاريخ الهيروغليفية استبدالالأرقام ضبابية مثل ظهور كل الحضارة المصرية. يعود تاريخ ميلادها إلى النصف الثاني من الألفية الثالثة قبل الميلاد. ويعتقد أن هذه الدقة في تلك الأيام كان تدبيرا ضروريا. كانت مصر بالفعل دولة كاملة وأصبحت كل عام أكثر قوة وواسعة. تم بناء المعابد ، وحفظ السجلات في الهيئات الإدارية الرئيسية ، ومن أجل الجمع بين كل هذا ، قررت السلطات إدخال نظام الحساب هذا. لقد كانت موجودة لفترة طويلة - حتى القرن العاشر الميلادي ، وبعدها استبدلها علم الهيراطيات.

الإنجاز الرئيسي لل قدماء المصريين في الرياضيات هوانها البساطة والدقة. بالنظر إلى الهيروغليفية ، كان من الممكن دائمًا تحديد عدد عشرات أو مئات أو الآلاف الذين تم تسجيلهم على ورق البردي. تعتبر ميزة أيضا نظام الجمع وضرب الأرقام. للوهلة الأولى فقط يبدو الأمر مربكًا ، ولكن بعد فهم الجوهر ، ستبدأ في حل مثل هذه المشكلات بسرعة وسهولة. تم التعرف على العيب كما ارتباك كبير. يمكن كتابة الأرقام ليس فقط في أي اتجاه ، ولكن أيضًا بشكل عشوائي ، لذلك استغرق الأمر وقتًا أطول لفك تشفيرها. وآخر ناقص ، ربما ، يكمن في سلسلة طويلة من الشخصيات بشكل لا يصدق ، لأنه كان لا بد من تكرارها باستمرار.


























