
Triangle er en af de mest almindeligegeometriske figurer, som vi allerede er bekendt med i grundskolen. Med spørgsmålet om hvordan man finder området i en trekant, møder hver skolelærer i geometriske lektioner. Så hvad er funktionerne ved at finde området i denne figur kan skelnes fra? I denne artikel vil vi gennemgå de grundlæggende formler, der er nødvendige for at udføre denne opgave, og vi vil også se på typer trekanter.

Du kan finde området af en trekant på helt forskellige måder, fordi i geometri er der ikke en slags figur, der indeholder tre vinkler. Disse typer omfatter:
Lad os overveje mere detaljeret hver af de eksisterende typer trekanter.

En sådan geometrisk figur betragtes som den mestfælles for at løse geometriske problemer. Når der er behov for at tegne en vilkårlig trekant, kommer denne mulighed til undsætning.
I den akutvinklede trekant, som navnet antyder, er alle vinkler skarpe og i alt 180 °.
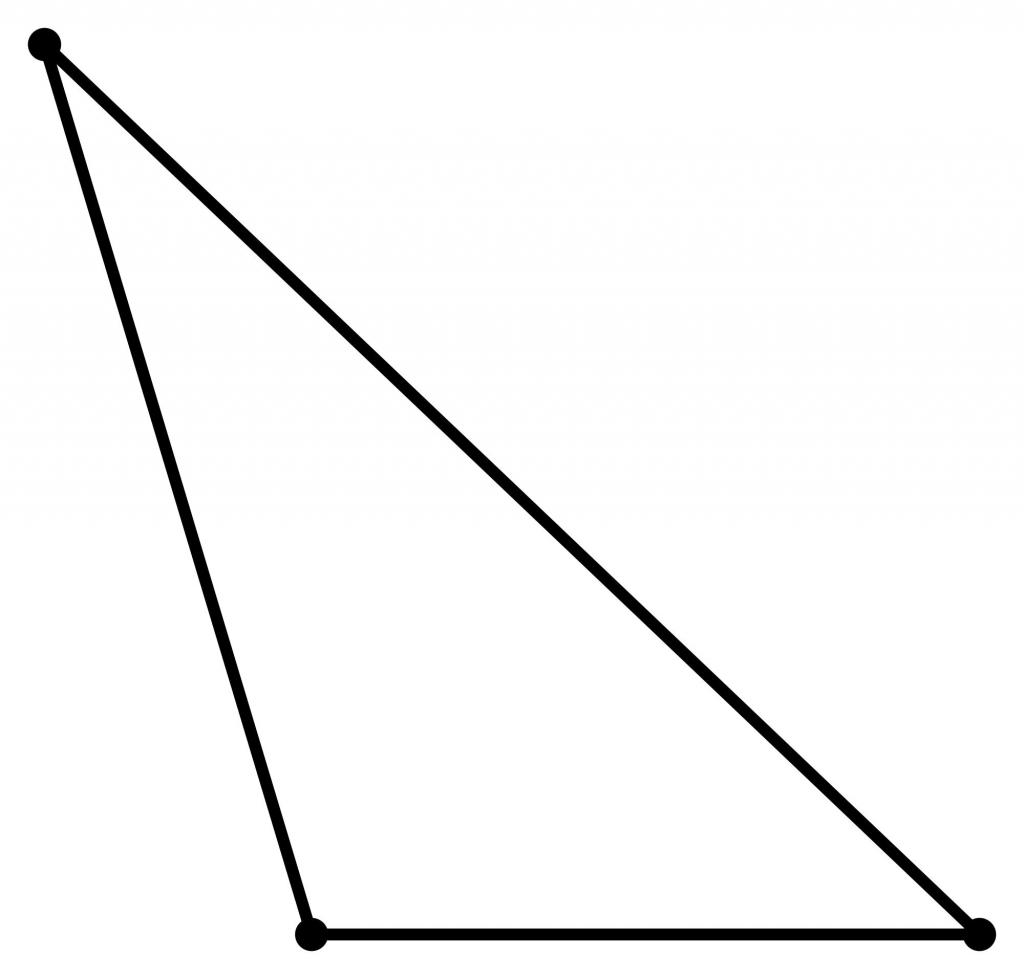
En sådan trekant er også meget almindelig,Det forekommer dog noget mindre ofte end akut. For eksempel er der ved kendelsen af trekanter (dvs. flere af siderne og vinklerne kendt, og det er nødvendigt at finde de resterende elementer), nogle gange er det nødvendigt at bestemme, om vinklen er stump eller ej. Cosinus af den stump vinkel er et negativt tal.
Størrelsen af en stump trekant en af vinklerne overstiger 90 °, så de resterende to hjørner kan tage små værdier (fx 15 ° eller endog 3 °).
For at finde området af en trekant af denne type, skal du kende nogle nuancer, som vi snakker om yderligere.
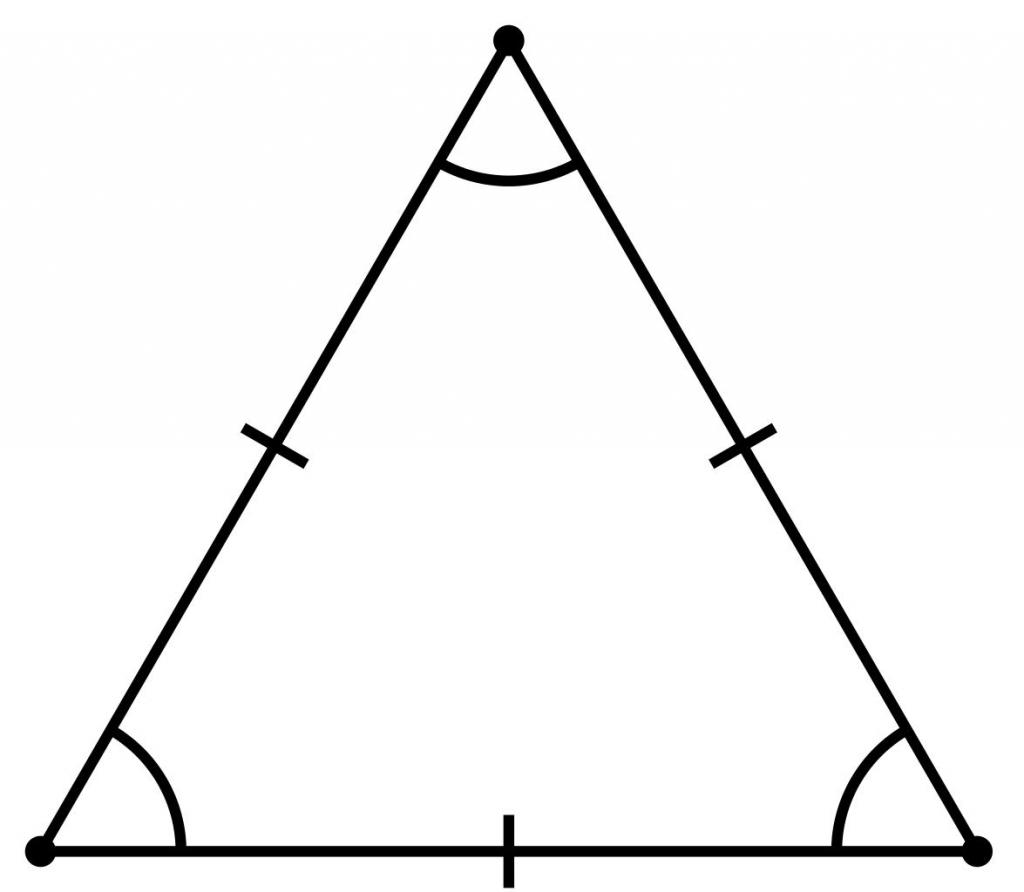
En almindelig polygon er en figur,Herunder n vinkler, hvor alle sider og vinkler er ens. Så er den rigtige trekant. Da summen af alle trekantets vinkler er 180 °, er hver af de tre vinkler 60 °.
Den rigtige trekant på grund af sin egenskab kaldes også en ligesidet figur.
Det er også værd at bemærke, at kun en cirkel kan skrives i en regelmæssig trekant, og kun en cirkel kan beskrives nær det, og deres centre er placeret på samme punkt.

Ud over den ligesidede type kan man også udstilleen ensartet trekant, lidt anderledes end den. Denne to sider af trekanten, og de to vinkler er lige, men den tredje side (støder op til hvilken de ens vinkler) er en base.
Figuren viser en ensartet trekant DEF, hvis vinkler D og F er ens, og DF er basen.

En rektangulær trekant hedder det, fordi en af sine hjørner er en lige linje, det vil sige 90 °. De to andre vinkler i alt er 90 °.
Den største side af en sådan trekant, som ligger modsat 90 ° vinklen, er hypotenusen, mens de to andre sider er benene. For en given type trekant er den pythagoriske sætning gældende:
Summen af kvadraterne af længderne af benene er lig med kvadratet af længden af hypotenusen.
Figuren viser den rektangulære trekant BAC med hypotenuse AC og benene AB og BC.
For at finde området af en trekant med en ret vinkel, skal du kende de numeriske værdier af benene.
Lad os videresende til formlerne for at finde området for en given figur.
I geometri kan man skelne mellem to formler somer egnede til at finde området for de fleste typer trekanter, nemlig for en akut vinklet, stump, regelmæssig og ensartet trekanter. Vi vil analysere hver enkelt af dem.
Denne formel er universel tilfinde området, den figur vi overvejer. For at gøre dette er det tilstrækkeligt at kende længden af siden og længden af højden til den. Formlen selv (halvdelen af produktet fra bunden til højden) ser sådan ud:
S = ½ * A * H,
hvor A er siden af denne trekant, og H er højden af trekanten.

For eksempel at finde området for den akutte vinklede trekant ACB, skal du multiplicere sin side AB ved CD'ens højde og dividere den resulterende værdi med to.
Det er dog ikke altid let at finde et områdetrekant på denne måde. For eksempel for at bruge denne formel for stump trekant, er det nødvendigt at fortsætte en af sine sider, og først derefter at holde det høje.
I praksis anvendes denne formel oftere end andre.
Denne formel, som den foregående, passer tilde fleste trekanter og i sin betydning er en følge af formlen for at finde området langs sidens og højden af trekanten. Det vil sige, at formlen under overvejelse let kan afledes af den foregående. Dens formulering ser sådan ud:
S = ½ * sinO * A * B,
hvor A og B er siderne af trekanten, og O er vinklen mellem siderne A og B.
Husk, at vinklenes sind kan ses i et specielt bord opkaldt efter den fremragende sovjetiske matematiker V. M. Bradis.
Og nu vender vi os til andre formler, der kun er egnede til ekstraordinære typer trekanter.
Udover den universelle formel, herunder behovet for at tegne en højde i en trekant, kan området af en trekant med en ret vinkel findes fra benene.
Således er området af en trekant med en ret vinkel halvdelen af dets ben, eller:
S = ½ * a * b,
hvor a og b er benene i en rigtig trekant.
Denne slags geometriske figurer adskiller sig i det,at dets område kan findes ved den angivne værdi af kun den ene side af den (da alle sider af den regulære trekant er ens). Så har vi opfyldt opgaven med at "finde et område af en trekant, når siderne er ens", skal vi bruge følgende formel:
S = A2* √3 / 4,
hvor A er siden af en ligesidet trekant.
Den sidste mulighed for at finde området i trekanten er Herons formel. For at kunne bruge det, skal du vide længden af de tre sider af figuren. Herons formel ser sådan ud:
S = √p · (p - a) · (p - b) · (p - c),
hvor a, b og c er siderne af denne trekant.
Nogle gange er problemet givet:"Området i den højre trekant er at finde længden af sin side". I dette tilfælde skal vi bruge formlen til at finde det område af en almindelig trekant, der allerede er kendt for os, og udlede af siden værdien af siden (eller dens firkant):
En2 = 4S / √3.
I GIA's problemer i matematik er der mange formler. Derudover er det ofte nødvendigt at finde området af en trekant på rutet papir.
I dette tilfælde er det mest hensigtsmæssigt at tegne en højde til den ene side af figuren, bestemme længden af figuren af cellerne og brug den universelle formel til at finde området:
S = ½ * A * H.
Så efter at have studeret den indsendte artikel i formlerne, du ikke har nogen problemer med at finde arealet af en trekant af nogen art.


























