
Cualquiera que haya pensado alguna vezPara convertirse en un especialista de TI o administrador del sistema, y simplemente para conectar el destino con la tecnología informática, es absolutamente necesario saber cómo se representan los números en la memoria de la computadora. Después de todo, es en esto en lo que se basan los lenguajes de programación de bajo nivel como Assembler. Por lo tanto, hoy consideraremos la representación de números en una computadora y su ubicación en las celdas de memoria.

Si está leyendo este artículo, lo más probableYa lo sé, pero vale la pena repetirlo. Todos los datos en una computadora personal se almacenan en un sistema de números binarios. Esto significa que cualquier número debe representarse en la forma adecuada, es decir, que consta de ceros y unos.
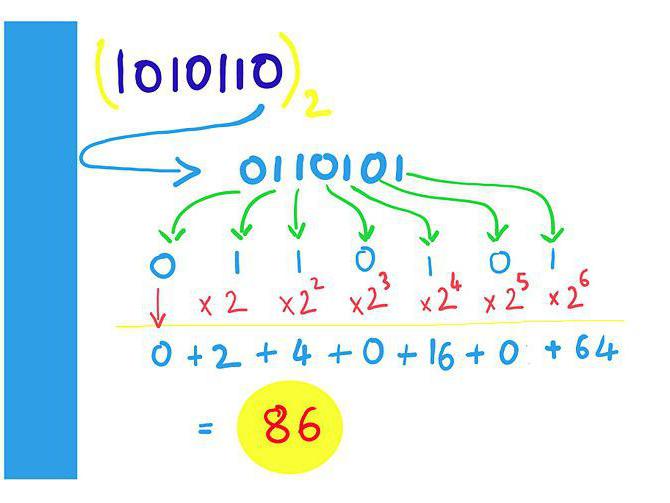
Para traducir los números decimales habituales a una forma que sea comprensible para una computadora, debe usar el algoritmo que se describe a continuación. También hay calculadoras especializadas.
Итак, для того чтобы перевести число в двоичную sistema numérico, debe tomar el valor que seleccionamos y dividirlo entre 2. Después de eso, obtenemos el resultado y el resto (0 o 1). Divide el resultado nuevamente 2 y recuerda el resto. Este procedimiento debe repetirse hasta que al final también haya 0 o 1. Luego anotamos el valor final y los residuos en el orden inverso, tal como los recibimos.
Así es como ocurre la representación de números en una computadora. Cualquier número se escribe en forma binaria y luego ocupa una celda de memoria.

Como ya deberías saber, el mínimoLa unidad de información es de 1 bit. Como ya hemos descubierto, la representación de números en una computadora tiene lugar en formato binario. Por lo tanto, cada bit de memoria estará ocupado por un valor: 1 o 0.
Las celdas se utilizan para almacenar grandes cantidades.Cada unidad de este tipo contiene hasta 8 bits de información. Por lo tanto, podemos concluir que el valor mínimo en cada segmento de memoria puede ser 1 byte o ser un número binario de ocho dígitos.
Finalmente, llegamos a la colocación directa de datos en la computadora. Como ya se mencionó, el procesador primero convierte la información en formato binario, y solo luego la coloca en la memoria.
Начнем мы с самого простого варианта, коим es una representación de enteros en una computadora. La memoria de la PC toma una cantidad ridículamente pequeña de celdas para este proceso, solo una. Por lo tanto, el máximo en una ranura puede ser valores de 0 a 11111111. Transfieramos el número máximo a la forma habitual de escritura.
X = 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 1 × 28 - 1 = 255.
Ahora vemos que en una celda de memoria puederango de 0 a 255. Sin embargo, esto se aplica exclusivamente a enteros no negativos. Si la computadora necesita escribir un valor negativo, todo irá un poco diferente.

Теперь давайте посмотрим, как происходит representación de números en una computadora si son negativos. Para colocar un valor menor que cero, se asignan dos celdas de memoria o 16 bits de información. En este caso, 15 van debajo del número mismo, y el primer bit (el más a la izquierda) se da debajo del signo correspondiente.
Si el número es negativo, se escribe "1", si es positivo, entonces "0". Para facilitar la memorización, podemos dibujar una analogía: si hay un signo, entonces ponga 1, si no es así, entonces nada (0).
Los 15 bits restantes de información se asignan al número.Similar al caso anterior, puede poner un máximo de quince unidades en ellos. Vale la pena señalar que escribir números negativos y positivos es significativamente diferente entre sí.
Para colocar en 2 ubicaciones de memoriavalor mayor o igual a cero, se utiliza el llamado código directo. Esta operación se realiza de la misma manera que se describió, y el máximo es A = 32766, si utiliza el sistema de números decimales. Solo quiero notar que en este caso, "0" se refiere a positivo.
La representación de enteros en la memoria de la computadora no esEs una tarea tan difícil. Aunque es un poco más complicado cuando se trata de un valor negativo. Para escribir un número que es menor que cero, se usa un código adicional.
Para obtenerlo, la máquina realiza una serie de operaciones auxiliares.
Damos un claro ejemplo.Supongamos que tenemos el número X = - 131. Primero obtenemos su módulo | X | = 131. Luego lo traducimos a un sistema binario y lo escribimos en 16 celdas. Obtenemos X = 0000000010000011. Después de invertir X = 1111111101111100. Agregue "1" y obtenga el código de retorno X = 1111111101111101. Para escribir en una celda de memoria de 16 bits, el número mínimo es X = - (215) = - 32767.
Как видите, представление вещественных чисел в La computadora no es tan difícil. Sin embargo, el rango considerado puede no ser suficiente para la mayoría de las operaciones. Por lo tanto, para acomodar grandes números, la computadora asigna 4 celdas, o 32 bits, de la memoria.
El proceso de grabación no es absolutamente diferente de lo anterior. Entonces, solo damos un rango de números que se pueden almacenar en este tipo.
Xmax= 2.147.483.647.
Xmin= - 2,147,483,648.

En la mayoría de los casos, estos valores son suficientes para registrar y realizar operaciones de datos.
Representación de números reales en una computadoraTiene sus ventajas y desventajas. Por un lado, esta técnica facilita la realización de operaciones entre valores enteros, lo que acelera enormemente el procesador. Por otro lado, este rango no es suficiente para resolver la mayoría de los problemas de economía, física, aritmética y otras ciencias. Por lo tanto, ahora consideraremos la siguiente técnica para super-cantidades.
Это последнее, что вам необходимо знать про representación de números en una computadora. Dado que el problema de determinar la posición de la coma en ellos surge cuando se escriben fracciones, se usa una forma exponencial para colocar dichos números en la computadora.
Cualquier número puede representarse en la siguiente forma X = m * pn. Donde m es la mantisa del número, p es la base del sistema numérico yn es el orden del número.
Para estandarizar la notación de números de coma flotante, se usa la siguiente condición, según la cual el módulo mantissa debe ser mayor o igual a 1 / ny menor que 1.
Se nos dará el número 666.66. Lo llevamos a forma exponencial. Resulta que X = 0.66666 * 103. P = 10 yn = 3.
Por lo general, 4 u 8 bytes (32 o 64 bits) se asignan para almacenar valores de coma flotante. En el primer caso, esto se denomina número de precisión ordinaria, y en el segundo, precisión doble.
De los 4 bytes asignados para almacenar dígitos, 1 (8bits) se proporciona para los datos en el orden y su signo, y 3 bytes (24 bits) van al almacenamiento de la mantisa y su signo de acuerdo con los mismos principios que para los valores enteros. Sabiendo esto, podemos hacer cálculos simples.
El valor máximo de n = 11111112 = 12710. En base a esto, podemos obtener el tamaño máximo de un número que puede almacenarse en la memoria de la computadora. X = 2127. Ahora podemos calcular la máxima mantisa posible. Ella será igual a 223 - 1 ≥ 223 = 2(10 × 2.3) ≥ 10002,3 = 10(3 × 2,3) ≥ 107. Como resultado, obtuvimos un valor aproximado.
Si ahora combinamos ambos cálculos, obtenemos un valor que puede registrarse sin pérdida en 4 bytes de memoria. Será igual a X = 1,701411 * 1038. Se descartaron los números restantes, ya que es precisamente esta precisión la que permite este método de grabación.

Como todos los cálculos fueron programados yexplicado en el párrafo anterior, aquí te lo diremos muy brevemente. Para números de doble precisión, generalmente se asignan 11 dígitos para el pedido y su signo, así como 53 dígitos para la mantisa.
P = 11111111112 = 102310.
M = 252 -1 = 2(10 * 5.2) = 10005.2 = 1015.6. Redondeamos y obtenemos el número máximo X = 21023 precisa a "m".
Esperamos que la información sobre la representación de números enteros y números reales en una computadora que hemos proporcionado le sea útil en el entrenamiento y sea al menos un poco más clara de lo que generalmente se escribe en los libros de texto.


























