
Jos vaihtovirta on kytkettysitten vastus, niin virta ja jännite piirissä missä tahansa aikakaavion pisteessä ovat verrannollisia toisiinsa. Tämä tarkoittaa, että virran ja jännitteen käyrät saavuttavat “huipun” arvon samanaikaisesti. Teemme näin, sanomme, että virta ja jännite ovat vaiheessa.
Harkitsemme nyt, kuinka vaihtovirtapiirin kondensaattori käyttäytyy.

Jos se on kytketty vaihtojännitelähteeseenKondensaattorin päällä olevan jännitteen maksimiarvo on verrannollinen piirissä virtaavan virran maksimiarvoon. Huippuaaltojännitteen sinusoidi ei kuitenkaan tapahdu samanaikaisesti suurimman virran kanssa.
Tässä esimerkissä hetkellinen virta saavuttaasen maksimiarvosta neljäsosa jaksosta (90 astetta) aikaisemmin kuin jännite. Tässä tapauksessa he sanovat, että "virta on 90 ° edellä jännitettä".
Toisin kuin tasavirtapiirin tilanne,V / I-arvo ei ole tässä vakio. Suhde Vmax / Imax on kuitenkin erittäin hyödyllinen määrä ja sähkötekniikassa sitä kutsutaan komponentin kapasitanssiksi (Xc). Koska tämä arvo heijastaa edelleen jännitteen ja virran suhdetta, ts. fyysisessä mielessä on vastus, sen mittayksikkö on ohmi. Kondensaattorin Xc arvo riippuu sen kapasitanssista (C) ja vaihtovirtataajuudesta (f).
Koska kondensaattori vaihtovirtapiirissäkun rms-jännitearvoa käytetään, sama vaihtovirta virtaa tässä piirissä, jota kondensaattori rajoittaa. Tämä rajoitus johtuu kondensaattorin reaktanssista.

Siksi nykyisen arvon piirissä, joka ei sisällä muita komponentteja paitsi kondensaattoria, määritetään Ohmin lain vaihtoehtoisella versiolla
jaRMS = YRMS / XC
Missä sinäRMS - neliökeskiarvon (tehollinen) jännitearvo. Huomaa, että Xkanssa korvaa R: n Ohmin lain DC-versiossa.
Nyt näemme, että piirin kondensaattoriVaihtovirta käyttäytyy täysin eri tavalla kuin jatkuva vastus, ja tilanne tässä vastaavasti on monimutkaisempi. Tällaisessa ketjussa esiintyvien prosessien ymmärtämiseksi on hyödyllistä ottaa käyttöön tällainen käsite vektorina.
Vektorin pääidea on ajatus siitäettä aikamuuttuvan signaalin kompleksiarvo voidaan esittää kompleksiluvun (joka ei riipu ajasta) ja jonkin ajan funktiona olevan kompleksisen signaalin tulona.
Voimme esimerkiksi edustaa funktiota A cos (2πνt + a) yksinkertaisesti kompleksina vakiona A ∙ ejΘ .
Koska vektoreita edustaa suuruus (tai moduuli) ja kulma, ne esitetään graafisesti nuolella (tai vektorilla), joka pyörii XY-tasossa.
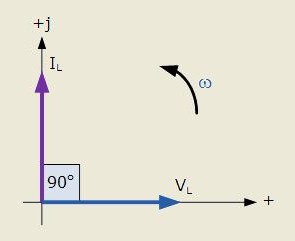
Ottaen huomioon, että jännite kondensaattorin yli"Viiveellä" suhteessa virtaan niitä edustavat vektorit sijaitsevat kompleksitasossa, kuten yllä olevassa kuvassa on esitetty. Tässä kuvassa virta- ja jännitevektorit pyörivät vastakkaiseen suuntaan myötäpäivään.
Esimerkissämme kondensaattorin virta johtuusen säännöllinen lataus. Koska vaihtovirtapiirin kondensaattorilla on kyky kerätä ja purkaa jaksoittain sähkövaraus, sen ja virtalähteen välillä tapahtuu jatkuva energianvaihto, jota sähkötekniikassa kutsutaan reaktiiviseksi energiaksi.


























