Série Maclaurin et extension de certaines fonctions

Изучающим высшую математику должно быть известно, que la somme d'une certaine série de puissance appartenant à l'intervalle de convergence d'une série donnée se révèle être une fonction continue et illimitée de fois différenciée. La question se pose: est-il possible de dire qu'une fonction arbitraire donnée f (x) est la somme d'une certaine série de puissance? Autrement dit, dans quelles conditions la fonction f (x) peut-elle être représentée par une série de puissances? L'importance de cette question est qu'il est possible de remplacer approximativement f-ju f (x) par la somme des premiers termes de la série de puissance, c'est-à-dire par un polynôme. Un tel remplacement d'une fonction par une expression assez simple - un polynôme - est pratique pour résoudre certains problèmes d'analyse mathématique, à savoir pour résoudre des intégrales, pour calculer des équations différentielles, etc.

Il est prouvé que pour certains f-ii f (x) dans lesquels il est possible de calculer des dérivées jusqu'au (n + 1) -ème ordre, y compris le dernier, dans un voisinage de (α - R; x₀ + R) d'un point x = α, la formule suivante est valable:

Cette formule tire son nom de la célèbre scientifique Brooke Taylor. La série obtenue à partir de la précédente s'appelle la série Maclaurin:

La règle qui permet d'effectuer l'extension dans la série Maclaurin:

1. Déterminez les dérivées des premier, deuxième, troisième ... ordres.
2. Calculez ce que les dérivées de x = 0 sont égales.
3. Écrivez la série Maclaurin pour cette fonction, puis déterminez l'intervalle de sa convergence.
4. Déterminer l'intervalle (-R; R) où le reste de la formule de Maclaurin

R_M.(x) -> 0 comme n -> infini. S'il en existe une, la fonction f (x) doit coïncider avec la somme des séries de Maclaurin.

Nous considérons maintenant la série Maclaurin pour les fonctions individuelles.

1. Donc, le premier sera f (x) = e^x. Bien sûr, en termes de caractéristiques, une telle fonction a des dérivées d'ordres très différents, et f^(k)(x) = e^avec, où k est égal à tous les nombres naturels. Remplacez x = 0. Nous obtenons f^(k)(0) = e⁰= 1, k = 1,2 ... Sur la base de ce qui précède, la série e^x ressemblera à ceci:

2. Série de Maclaurin pour la fonction f (x) = sin x. Clarifions tout de suite que la fonction pour toutes les inconnues aura des dérivés; de plus, f^"(x) = cos x = sin (x + n / 2), f^""(x) = -sin x = sin (x + 2 * n / 2) ..., f^(k)(x) = sin (x + k * n / 2), où k est égal à tout nombre naturel. Autrement dit, après avoir fait des calculs simples, nous pouvons arriver à la conclusion que la série pour f (x) = sin x sera de cette forme:

3. Essayons maintenant de considérer f-yu f (x) = cos x. Pour toutes les inconnues, il a des dérivés d'ordre arbitraire, et | f^(k)(x) | = | cos (x + k * n / 2) | <= 1, k = 1.2 ... Encore une fois, après avoir effectué certains calculs, nous obtenons que la série pour f (x) = cos x ressemblera à ceci:

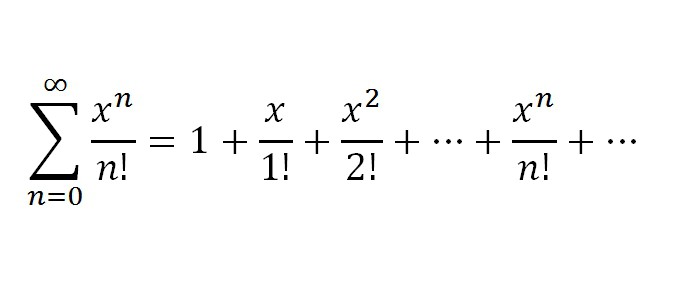
Nous avons donc répertorié les fonctions les plus importantespeuvent être étendus dans une série Maclaurin, mais ils sont complétés par la série Taylor pour certaines fonctions. Maintenant, nous allons les énumérer également. Il convient également de noter que les séries de Taylor et Maclaurin sont une partie importante de l'atelier de résolution de séries en mathématiques supérieures. Donc les rangs de Taylor.

1. Le premier sera une série pour f-ii f (x) = ln (1 + x).Comme dans les exemples précédents, pour un f (x) = ln (1 + x) donné, on peut ajouter la série en utilisant la forme générale de la série Maclaurin. cependant, la série Maclaurin peut être obtenue beaucoup plus simplement pour cette fonction. En intégrant une certaine série géométrique, on obtient une série pour f (x) = ln (1 + x) d'un tel échantillon:

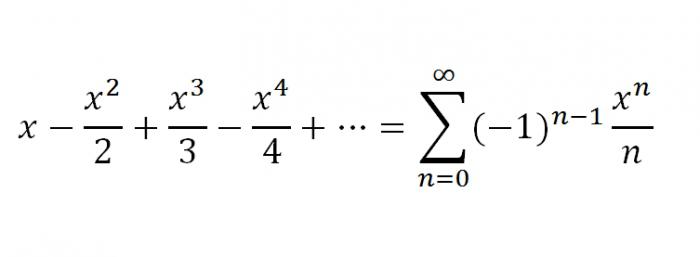
2. Et le second, qui sera définitif dans notre article, sera la série pour f (x) = arctan x. Pour x appartenant à l'intervalle [-1; 1], la décomposition est valide:

C'est tout. Cet article examine les séries de Taylor et Maclaurin les plus couramment utilisées en mathématiques supérieures, en particulier dans les universités d'économie et techniques.