
Le triangle est l'une des figures principales de la planimétrie.C'est avec lui dans le programme scolaire que commence l'étude de la géométrie réelle, en un sens, la géométrie. Selon le type de coins, ce type de forme peut être divisé en plusieurs types. Lors de la résolution de problèmes, le rectangulaire est généralement considéré comme le plus simple. Pour lui, il existe de nombreux théorèmes, règles, ainsi que des fonctions trigonométriques qui permettent de trouver n'importe quelle jambe ou hypoténuse, ne connaissant que la longueur d'un des côtés et l'angle (quel que soit sauf celui de droite).
Cependant, si seulement ce genre existaittriangles, la vie des collégiens et lycéens serait beaucoup plus facile et insouciante. Mais ce n'est pas le cas. Chaque figure que la géométrie étudie a ses propres caractéristiques et propriétés. Afin de résoudre les problèmes en toute confiance, vous devez connaître les propriétés de tous les polygones.

Un triangle isocèle ressemble beaucoup à un animal de compagniePythagore, qui a été mentionné dans l'introduction. Même un élève de cinquième comprendra les règles liées à sa construction ou à la recherche d'éléments inconnus. L'essentiel est de bien connaître les concepts de base de la géométrie et les éléments de base des figures plates.
Les propriétés d'un triangle isocèle flottentde sa structure. Les deux coins à la base d'un tel polygone sont les mêmes, de même que les côtés. Une certaine conclusion peut être tirée de ces informations. Afin de trouver la mesure en degré du sommet, connaissant l'un des angles de la base, vous devez le multiplier par deux et le soustraire de 180 °. Deux côtés, dont les points extrêmes sont en haut et en bas, sont appelés latéraux.
Ce chiffre n'a pas de règles en tant que tel - tout est entâches vient de sa construction, ce qui le rend compréhensible et pratique pour les étudiants. Cependant, il existe une caractéristique principale qui peut être appelée la propriété de la médiane d'un triangle isocèle. Tout est dans sa double nature. Si vous construisez un tel triangle sur papier selon toutes les règles, vous remarquerez que la ligne au centre n'est pas seulement la médiane, mais aussi la hauteur et la bissectrice.
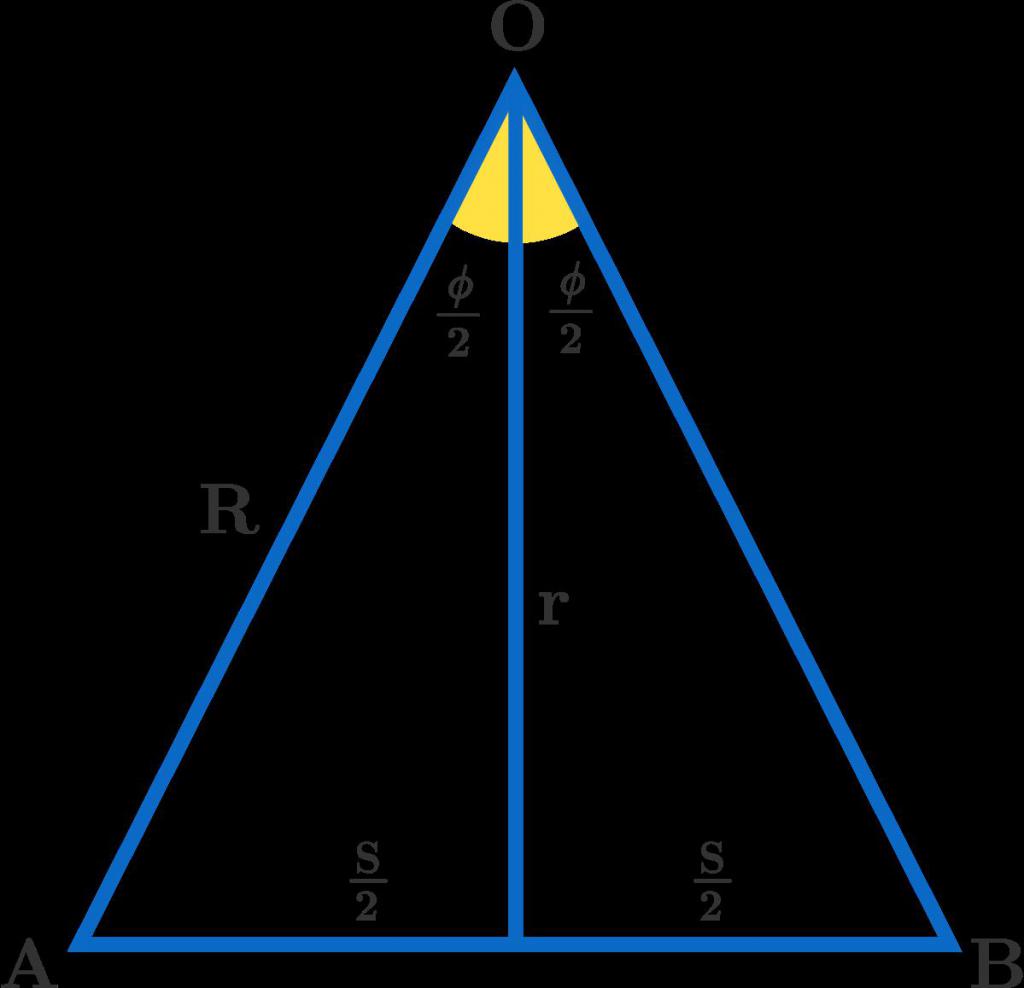
Une ligne droite tracée de haut en basne sera pas si univoque. Ses propriétés sont déterminées par les principales caractéristiques d'un triangle isocèle. Abaissé du coin du sommet à la base, il crée deux triangles égaux, et avec la base il forme une perpendiculaire qui le divise en segments égaux. Ce type de triangles ne doit pas être confondu avec les triangles équilatéraux (une telle erreur est souvent commise par les élèves). Ils ont trois coins identiques, pas deux comme ici.


























