
गिनती की आवश्यकता स्पष्ट हो गईआदिम समाज के गठन की शुरुआत से ही मनुष्य। उनकी संख्यात्मक प्रणाली, विशिष्ट संख्यात्मक पदनामों के साथ, सभ्यता के सभी अलग-अलग केंद्रों में बनाई गई थी: मिस्र और प्राचीन बाबुल में, चीन और भारत में, दक्षिण अमेरिकी भारतीयों में और प्राचीन ग्रीस में। गणित टोपोलॉजी में सबसे जटिल प्रमेयों के समाधान के लिए वस्तुओं की सबसे सरल गिनती से चला गया है। इसी समय, संख्या शून्य का इतिहास इस अवधि का केवल एक छोटा हिस्सा गिना जाता है।

लैटिन नूलिस से ("कोई नहीं") शब्द आता है,सबसे महत्वपूर्ण गणितीय अवधारणाओं में से एक को दर्शाते हुए। इसमें न केवल एक प्रतीक शामिल है - एक संख्या जो स्कोर रखने में मदद करती है, गणितीय कार्यों को लिखने के लिए। यह एक पूरी अवधारणा है। किसी भी मात्रा का अभाव, शून्यता, शुरुआत और अनन्तता - इन अवधारणाओं का दार्शनिक दृष्टिकोण अलग-अलग युगों में, विश्व दृष्टिकोण के विभिन्न प्रणालियों में अलग था।
प्रागैतिहासिक काल में, रेकिंग का नेतृत्व करेंउंगलियों और पैर की उंगलियों की मदद की। संख्याओं का विभाजन fives और दसियों में, दशमलव संख्या प्रणाली की उत्पत्ति इसके साथ जुड़ी हुई है। भविष्य में, इन ऑपरेशनों को सुविधाजनक बनाने के लिए, लकड़ी और जानवरों की हड्डियों पर notches, पत्थरों, कंकड़ पर notches का उपयोग किया गया था। गोले और अन्य छोटे आइटम। ऐसा प्रत्येक तत्व एक विशिष्ट संख्या का प्रतिनिधित्व करता है। सबसे व्यावहारिक संख्यात्मक मॉडल एक समान प्रकृति के हैं। ऐसी प्रणालियों को स्थितीय कहा जाता है - अंकों को लिखने का अर्थ उनकी स्थिति या रैंक से निर्धारित होता है।
दृष्टिकोण और लागू में विपरीत का एक उदाहरणअब तक, सिस्टम संख्या लिखने का एक तरीका है जो प्राचीन रोम के समय से नीचे आ गया है। यह इकाइयों, दसियों, सैकड़ों को नामित करने के लिए लैटिन वर्णमाला के अक्षरों का उपयोग करता है।

मतगणना बोर्ड, खांचे से मिलकर,कुछ श्रेणियों के अनुरूप, जिसमें कंकड़ या मोती रखे जाते हैं, विभिन्न लोगों और युगों की संस्कृतियों से परिचित होते हैं। अबेकस की अन्य किस्मों को जाना जाता है - मोतियों के साथ गाँठ या डोरियों के साथ रस्सियाँ। इस तरह के डिवाइस के विकास में अगला कदम एबेकस था, जिसका उपयोग कैलकुलेटर के आगमन से पहले किया गया था।
संख्या शून्य का इतिहास उत्पत्ति की एक प्रक्रिया हैगणितीय अवधारणा और प्रतीक के उपयोग की शुरुआत जो इसे दर्शाता है। अबेकस और अबेकस, एक अर्थ में, एक संख्या श्रृंखला की कल्पना करने का एक साधन है। इसी इंडेंटेशन में एक खाली स्थान या एक लापता एबेकस ने शून्य की अमूर्त अवधारणा को स्पष्ट कर दिया। इसके लिए प्रतीक पहले प्राचीन बाबुल के गणितज्ञों और खगोलविदों के बीच दिखाई दिया।

एक सभ्यता में टिगरिस और के बीच पैदा हुआयूफ्रेट्स, संख्या प्रणाली को अपनाया गया था, जो प्राचीन सुमेरियों से विरासत में मिला था। यह स्थितीय था - अन्य संख्याओं के सापेक्ष स्थिति पर निर्भर संख्याओं का अर्थ। 4-5 हजार साल ईसा पूर्व के लिए विकसित। ई।, यह 60 की संख्या पर बनाया गया था। प्राचीन बेबीलोन के इंजीनियरों और खगोलविदों द्वारा उपयोग की जाने वाली गणितीय गणना, इसलिए बल्कि बोझिल और असुविधाजनक लगती थी। संख्याओं के साथ सफलतापूर्वक संचालित करने के लिए, दिल से याद रखना आवश्यक था या आपकी आंखों के सामने सभी संख्याओं को 1 से 60 तक गुणा करने का परिणाम था।
शून्य संख्या, या बाबुल के लोगों द्वारा अपनाई गई निशानीडिस्चार्ज पदनाम दो वेजेज या एंगल पर सेट किए गए तीर की तरह लग रहे थे। यह प्रतीक संख्या का एक अभिन्न अंग था और अंकगणितीय कार्यों में भाग नहीं लेता था - इसके द्वारा जोड़ना या गुणा करना असंभव था।

मेसोपोटामिया के गणितज्ञों के स्वतंत्र रूप से, मध्य अमेरिका के भारतीयों - मायाओं और इंकाओं ने अपने शून्य को रोजमर्रा की जिंदगी में पेश किया। दोनों संख्या प्रणालियों के लिए सामान्य यह था कि उन्होंने शून्य के विचार को संख्या के रूप में विकसित नहीं किया था।
प्राचीन अमेरिकी सभ्यता दुनिया छोड़ गईबौद्धिक क्षेत्र में कई उपलब्धियां। Mayans और Incas के जटिल कैलेंडर सिस्टम खगोलीय टिप्पणियों और जटिल गणितीय गणना में अनुभव के सदियों का परिणाम हैं। लेकिन कभी भी उनके समीकरणों में अंक शून्य एक संख्या के रूप में मौजूद था जो गणितीय कार्यों के परिणाम को प्रभावित करता था।

प्राचीन ग्रीक गणितज्ञों की मुख्य विरासतज्यामिति और खगोल विज्ञान में उनकी उपलब्धियां थीं। उनके प्रतिनिधित्व में संख्याएं ऐसे खंड हैं जिनमें एक शुरुआत, एक अंत और एक निश्चित लंबाई है। शून्य एक संख्या है जिसका इस मामले में कोई व्यावहारिक मूल्य नहीं है। एक शून्य-लंबाई खंड प्राचीन गणित और दर्शन में कोई मतलब नहीं था।
अरस्तू की शिक्षाओं के मुख्य सिद्धांतों में से एकवाक्यांश नेचुरल एब्रहेट वैक्यूम है - "प्रकृति एक निर्वात का उल्लंघन करती है।" अनंत, कुछ भी नहीं, गैर-अस्तित्व - ये श्रेणियां प्राचीन ब्रह्मांड में फिट नहीं थीं। इसलिए, प्रश्न का आधुनिक अर्थ "क्या संख्या 0 है" आर्किमिडीज़, पाइथागोरस या यूक्लिड के लिए अप्राप्य थी, हालांकि महान खगोलविद् टॉलेमी की तालिकाओं में शून्य के समान एक प्रतीक पाया जाता है। "ओमिक्रॉन" अक्षर (शब्द में पहला अक्षर - "कुछ भी नहीं") उसने खाली कोशिकाओं में डाल दिया।
भारतीय गणितज्ञों ने क्या आविष्कार किया था?महावीर (vi५०), ब्रह्मगुप्त (१११४), अरिभट्ट (४ )६) ग्रंथों के लेखक हैं, जिसमें संख्याओं की रिकॉर्डिंग की आधुनिक प्रणाली और बुनियादी अंकगणितीय संचालन के नियमों ने बड़े पैमाने पर आकार लिया है। इतिहासकारों का मानना है कि दशमलव संख्या प्रणाली को भारतीयों ने चीनी और बाबुल के लोगों से लिया गया था। यह माना जाता है कि शून्य के लिए प्रतीक भी भारतीयों द्वारा टॉलेमी के कार्यों से उधार लिया गया था।
तैयार करने वाला पहला गणितज्ञएक पूर्ण संख्या प्रणाली, जो आज तक अपरिवर्तित बनी हुई है और अधिकांश मानवता की सेवा करती है, खोरज़मी मुहम्मद बिन मूसा (787-850) थे, जो बगदाद में रहते थे। उनकी भारतीय लेखा की पुस्तक में नौ अरबी अंकों का विवरण है और इस सवाल का जवाब है, "क्या एक संख्या है?" इस पुस्तक में शून्य का उल्लेख सबसे पहले माना जाता है। इस काम का लैटिन अनुवाद, बारहवीं शताब्दी में यूरोप में व्यापक रूप से जाना जाने लगा और पूर्वी गणितीय ज्ञान के प्रसार की नींव रखी।
यूरोपीय लोगों के विपरीत, पूर्वी लोगों में अनंत काल हैदार्शनिक विस्मय-विमुग्ध थे। इसलिए, प्राचीन भारतीय वैज्ञानिकों के समीकरणों में शून्य अंत में न केवल संबंधित श्रेणी में इकाइयों की अनुपस्थिति का प्रतीक बन गया, बल्कि एक प्राकृतिक संख्या भी है जो गणनाओं के परिणाम को प्रभावित करती है। शून्य को जोड़ना, 0 से गुणा करना - यह सब सार्थक गणितीय कार्यों का अर्थ प्राप्त कर चुका है।

1 से 0 तक की संख्याओं के लेखन ने अपने अंतिम रूप में ले लिया, प्राचीन भारतीय गणितीय ग्रंथों के लिए भी धन्यवाद, और उन प्रतीकों को जिन्हें आमतौर पर यूरोप में अरबी कहा जाता है, खुद को अरब द्वारा भारतीय कहा जाता है।
संख्या "शून्य" का इतिहास व्युत्पत्ति विज्ञान में परिलक्षित होता हैबुनियादी गणितीय शब्द। "अंक" शब्द की अरबी जड़ें हैं और यह शब्द "अल-सिफर" से आया है, जिसका अर्थ है "खाली, शून्य"। अंग्रेजी "शून्य" अस्पष्ट "मार्शमैलो" जैसा दिखता है - पूर्व से हवा - यह पूर्व से था कि अंतिम, तर्कसंगत और सुविधाजनक संख्या प्रणाली यूरोप में आई थी।
मुख्य यूरोपीय प्रचारकों में से एकप्रसिद्ध इतालवी गणितज्ञ लियोनार्डो फाइबोनैचि अरबी डिजिटल प्रणाली बन गए। उनके काम "द बुक ऑफ अबैकस" (1202) ने यूरोपीय वैज्ञानिकों को उन प्रतीकों और नियमों से परिचित कराया जिनके द्वारा अरब गणितीय संचालन लिखते हैं। पूर्वी गणितीय मॉडल की सुविधा और तर्कसंगतता की सराहना करने वाले पहले वे संख्याओं के दैनिक हैंडलिंग के आदी थे - बैंकर और व्यापारी। उन्होंने अरब व्यापारियों से संख्या प्रणाली और अंकों के लेखन को जल्दी से अपनाया। लेकिन यूरोप के वैज्ञानिक व्यवहार में, यूरोपीय गणितज्ञों द्वारा अपनाई गई प्राचीन प्रणाली की जगह, यह ज्ञान केवल 4 शताब्दियों के बाद दृढ़ता से दर्ज किया गया था।
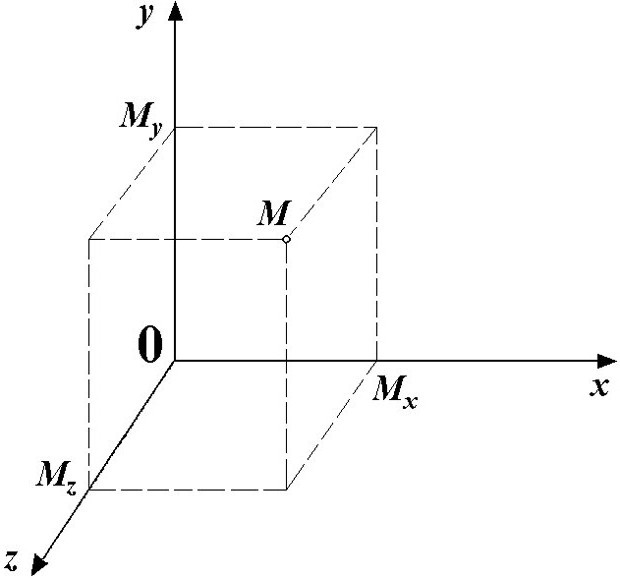
शून्य ने वैज्ञानिकता के परिचय के साथ महत्व प्राप्त कियारेने डेकार्टेस द्वारा 17 वीं शताब्दी में प्रस्तावित आयताकार समन्वय प्रणाली का उपयोग। केंद्र में स्थित शून्य ने तीन समन्वय अक्षों के एक दृश्यमान और दृश्यमान रूप से समझने योग्य संदर्भ बिंदु का अर्थ प्राप्त कर लिया है।
रूस में, प्रसिद्ध पाठ्यपुस्तक "अंकगणित, अर्थात् संख्याओं का विज्ञान" (1703) के लेखक लिओन्टी मैग्निटस्की के प्रयासों के माध्यम से शून्य को व्यवहार में लाया गया था।
शून्य जो सकारात्मक और के बीच अंतर करता हैनकारात्मक संख्याओं में अद्वितीय गणितीय गुण होते हैं। यह एक समान, अहस्ताक्षरित प्राकृतिक पूर्णांक है। शून्य के साथ जोड़ना और शून्य को घटाना किसी भी तरह से संख्या को प्रभावित नहीं करता है, और 0 से गुणा करना शून्य देता है। शून्य द्वारा विभाजन को एक अर्थहीन ऑपरेशन माना जाता है, जिसे यदि कंप्यूटर प्रोग्राम में निष्पादित किया जाता है, तो सिस्टम को महत्वपूर्ण नुकसान हो सकता है।
यह 0 से विभाजित करने के प्रयास में था कि विफलता का अर्थ निकलायूएस नेवी क्रूजर यॉर्कटाउन के कंप्यूटर सिस्टम में, जो 1997 के पतन में हुआ और प्रोपल्शन सिस्टम के अनधिकृत बंद के कारण हुआ। संख्या "कुछ भी नहीं" के प्रति गलत दृष्टिकोण ने एक शक्तिशाली युद्धपोत को असहाय स्थिर लक्ष्य में बदल दिया।
इस संख्या के मूल्य में काफी वृद्धि हुई हैविज्ञान का विकास। शून्य न केवल विशुद्ध रूप से गणितीय क्षेत्रों में उत्पन्न होता है। ध्वनिकी में श्रव्यता सीमा को 0. के रूप में लिया जाता है। कई माप उपकरणों के पैमाने की शुरुआत में कौन सी संख्या होती है, यह भी छात्र को ज्ञात होता है: 0 सेल्सियस के पैमाने पर पानी का हिमांक बिंदु होता है, देशांतर का मूल अभाज्य गुणांक है , आदि।
बाइनरी नोटेशन, जो कि आधार के रूप में कार्य करता हैआधुनिक कंप्यूटिंग उपकरणों का निर्माण, बेस दो के साथ एक स्थितीय संख्या प्रणाली है। इसका मतलब है कि कंप्यूटर सिस्टम में दर्ज सभी डेटा दो वर्णों के संयोजन से एन्कोडेड हैं - एक और शून्य।

आधुनिक दुनिया में कंप्यूटर की भूमिका जीवन के सभी पहलुओं के लिए निर्णायक होती जा रही है, जिसका अर्थ है कि शून्य का इतिहास, जिसके बिना उनकी उपस्थिति असंभव थी, जारी है।


























