
त्रिकोण सबसे आम में से एक हैज्यामितीय आकार, जिसके साथ हम प्राथमिक विद्यालय में परिचित हैं। एक त्रिकोण के क्षेत्र का पता लगाने का प्रश्न, प्रत्येक छात्र ज्यामिति पाठ में सामना करता है। तो, इस आंकड़े के क्षेत्र को खोजने की क्या विशेषताएं हैं? इस लेख में हम इस तरह के कार्य को करने के लिए आवश्यक बुनियादी सूत्रों को देखेंगे, साथ ही साथ त्रिकोण के प्रकारों का विश्लेषण करेंगे।

आप एक त्रिकोण के क्षेत्र को पूरी तरह से अलग-अलग तरीकों से पा सकते हैं, क्योंकि ज्यामिति में एक से अधिक प्रकार के आकार होते हैं जिनमें तीन कोने होते हैं। इन प्रकारों में शामिल हैं:
आइए हम प्रत्येक मौजूदा प्रकार के त्रिकोणों पर अधिक विस्तार से विचार करें।

इस तरह के एक ज्यामितीय आकार को सबसे अधिक माना जाता हैज्यामितीय समस्याओं को हल करने में आम। जब आवश्यकता एक मनमाना त्रिकोण खींचने के लिए उठती है, तो यह विकल्प है जो बचाव के लिए आता है।
तीव्र त्रिभुज में, जैसा कि नाम से पता चलता है, सभी कोण तेज हैं और 180 ° तक जुड़ जाते हैं।
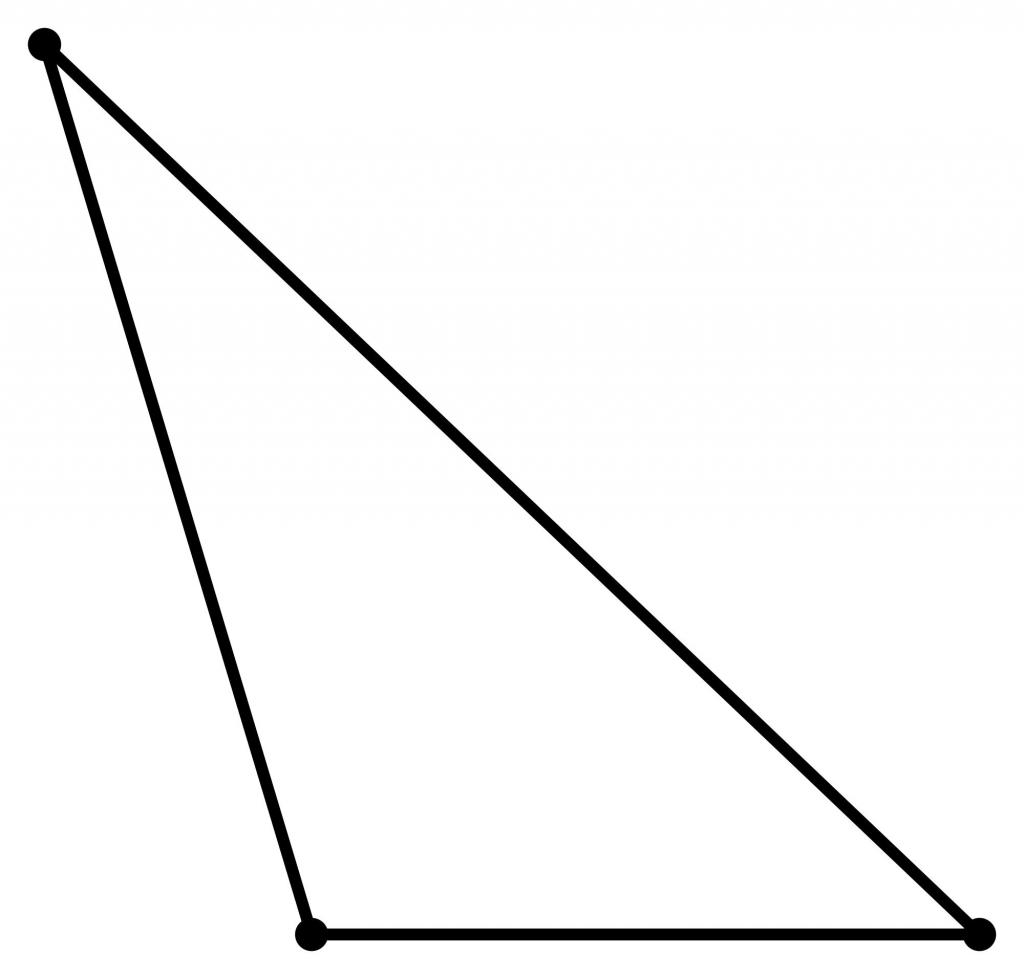
ऐसा त्रिभुज भी बहुत आम है,हालांकि, यह एक्यूट से कम आम है। उदाहरण के लिए, जब त्रिकोणों को हल करना (अर्थात, कई पक्ष और कोण ज्ञात होते हैं और शेष तत्वों को खोजने की आवश्यकता होती है) तो यह निर्धारित करना कभी-कभी आवश्यक होता है कि कोण तिरछा है या नहीं। प्रसूति कोण का कोसाइन एक ऋणात्मक संख्या है।
एक obtuse-angled त्रिकोण में, कोणों में से एक का परिमाण 90 ° से अधिक है, इसलिए शेष दो कोण छोटे मान ले सकते हैं (उदाहरण के लिए, 15 ° या 3 °)।
इस प्रकार के एक त्रिकोण के क्षेत्र को खोजने के लिए, आपको कुछ बारीकियों को जानने की जरूरत है, जिनके बारे में हम आगे चर्चा करेंगे।
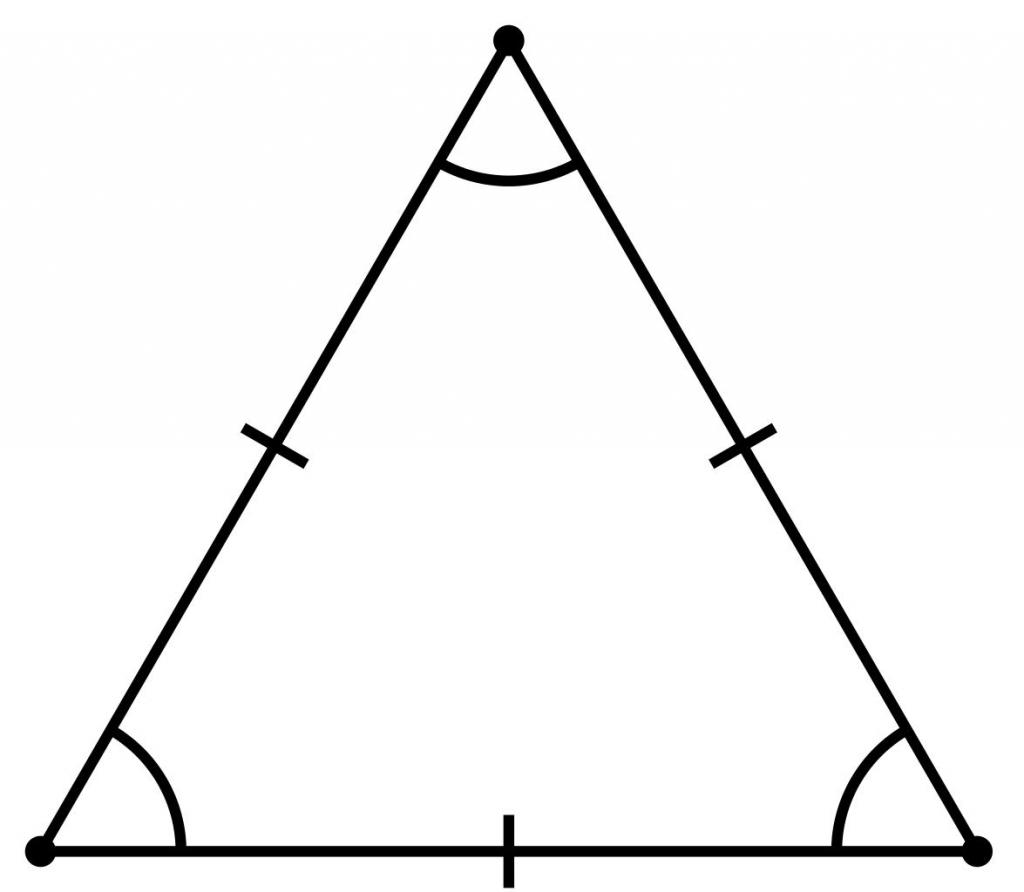
Правильным многоугольником называется фигура, इसमें एन कोने शामिल हैं, जिसमें सभी पक्ष और कोण समान हैं। यह सही त्रिकोण है। चूँकि त्रिभुज के सभी कोणों का योग 180 ° होता है, इसलिए तीनों कोणों में से प्रत्येक 60 ° होता है।
अपनी संपत्ति के कारण, नियमित त्रिभुज को एक समभुज आकृति भी कहा जाता है।
यह भी ध्यान देने योग्य है कि केवल एक वृत्त को एक नियमित त्रिभुज में अंकित किया जा सकता है और इसके चारों ओर केवल एक वृत्त का वर्णन किया जा सकता है, और उनके केंद्र एक बिंदु पर स्थित होते हैं।

समबाहु प्रकार के अलावा, आप हाइलाइट भी कर सकते हैंसमद्विबाहु त्रिकोण, इससे थोड़ा अलग। इस तरह के त्रिभुज में, दो भुजाएँ और दो कोण एक दूसरे के बराबर होते हैं, और तीसरा पक्ष (जिसके बराबर कोण झूठ बोलते हैं) आधार है।
आंकड़ा एक समद्विबाहु त्रिभुज DEF दिखाता है, जिनमें से कोण D और F समान हैं, और DF आधार है।

समकोण त्रिभुज इसलिए नाम दिया गया है क्योंकि इसका एक कोना सीधा है, अर्थात यह 90 ° के बराबर है। अन्य दो कोण 90 ° तक जुड़ते हैं।
इस तरह के त्रिभुज का सबसे बड़ा भाग, 90 ° के कोण के विपरीत स्थित है, कर्ण है, जबकि इसके दूसरे दो भाग पैर हैं। इस प्रकार के त्रिभुजों के लिए, पायथागॉरियन प्रमेय लागू होता है:
पैरों की लंबाई के वर्गों का योग कर्ण की लंबाई के वर्ग के बराबर है।
आंकड़ा कर्ण एसी और पैरों एबी और बीसी के साथ एक समकोण त्रिभुज बीएसी दिखाता है।
एक समकोण के साथ एक त्रिभुज का क्षेत्रफल ज्ञात करने के लिए, आपको इसके पैरों के संख्यात्मक मानों को जानना होगा।
आइए इस आकृति के क्षेत्र को खोजने के लिए सूत्रों पर चलते हैं।
ज्यामिति में, दो सूत्र भेद किए जा सकते हैं, जोअधिकांश प्रकार के त्रिभुजों के क्षेत्र को खोजने के लिए उपयुक्त हैं, अर्थात् तीव्र कोण वाले, मोटे, नियमित और समद्विबाहु त्रिभुजों के लिए। आइए उनमें से प्रत्येक का विश्लेषण करें।
यह सूत्र सर्वव्यापी हैजिस आंकड़े पर हम विचार कर रहे हैं उसका क्षेत्रफल ज्ञात करना। ऐसा करने के लिए, यह पक्ष की लंबाई और उसके पास खींची गई ऊंचाई की लंबाई जानने के लिए पर्याप्त है। सूत्र स्वयं (आधार और ऊंचाई का आधा उत्पाद) इस तरह दिखता है:
एस = A * ए * एच,
जहाँ A दिए गए त्रिभुज की भुजा है और H त्रिभुज की ऊँचाई है।

उदाहरण के लिए, एक तीव्र-कोण त्रिभुज एसीबी के क्षेत्र को खोजने के लिए, ऊँचाई सीडी द्वारा इसके किनारे एबी को गुणा करें और परिणामी मान को दो से विभाजित करें।
हालांकि, क्षेत्र को ढूंढना हमेशा आसान नहीं होता हैइस तरह से त्रिकोण। उदाहरण के लिए, एक सूत्र त्रिकोण के लिए इस सूत्र का उपयोग करने के लिए, आपको इसके पक्षों में से एक को जारी रखने की आवश्यकता है और उसके बाद ही ऊंचाई को आकर्षित करें।
व्यवहार में, यह सूत्र दूसरों की तुलना में अधिक बार उपयोग किया जाता है।
यह सूत्र, पिछले एक की तरह, के लिए उपयुक्त हैअधिकांश त्रिभुज और इसके अर्थ में त्रिभुज की भुजा और ऊँचाई द्वारा क्षेत्रफल ज्ञात करने के सूत्र का परिणाम है। अर्थात्, माना गया सूत्र आसानी से पिछले एक से प्राप्त किया जा सकता है। इसका शब्दांकन इस तरह दिखता है:
S = sin * sinO * A * B,
जहाँ A और B त्रिभुज की भुजाएँ हैं और O भुजा A और B के बीच का कोण है।
स्मरण करो कि एक कोण की साइन को विशेष सोवियत गणितज्ञ वी.एम. ब्रैडिस के नाम पर एक विशेष तालिका में देखा जा सकता है।
अब आइए अन्य सूत्रों पर चलते हैं जो केवल असाधारण प्रकार के त्रिकोणों के लिए उपयुक्त हैं।
सार्वभौमिक सूत्र के अलावा, जिसमें एक त्रिभुज में ऊँचाई खींचने की आवश्यकता शामिल है, एक त्रिभुज का क्षेत्रफल जिसमें समकोण होता है, अपने पैरों से पाया जा सकता है।
तो, एक समकोण वाला त्रिभुज का क्षेत्रफल उसके पैरों का आधा उत्पाद है, या:
एस = a * ए * बी,
जहाँ a और b एक समकोण त्रिभुज के पैर हैं।
Данный вид геометрических фигур отличается тем, इसका क्षेत्र उसके केवल एक पक्ष के संकेतित मूल्य के लिए पाया जा सकता है (चूंकि एक नियमित त्रिभुज के सभी पक्ष समान हैं)। तो, समस्या का सामना "पक्षों के बराबर होने पर एक त्रिभुज का क्षेत्रफल ज्ञात करें", आपको निम्न सूत्र का उपयोग करने की आवश्यकता है:
स = अ2* 43/4,
जहाँ A एक समबाहु त्रिभुज की भुजा है।
त्रिकोण का क्षेत्र खोजने का अंतिम विकल्प हेरॉन का सूत्र है। इसका उपयोग करने के लिए, आपको आंकड़े के तीन किनारों की लंबाई जानने की आवश्यकता है। बगुला का सूत्र इस तरह दिखता है:
एस = --p (पी - ए) (पी - बी) (पी - सी),
जहाँ a, b और c इस त्रिभुज की भुजाएँ हैं।
कभी-कभी समस्या दी जाती है:"एक नियमित त्रिभुज का क्षेत्रफल - इसकी भुजा की लंबाई ज्ञात करें"। इस मामले में, आपको एक नियमित त्रिकोण के क्षेत्र को खोजने के लिए पहले से ही ज्ञात सूत्र का उपयोग करने की आवश्यकता है और इससे प्राप्त पक्ष (या इसके वर्ग) का मान:
एक2 = 4S / √3।
गणित में जीआईए की समस्याओं में, कई सूत्र हैं। इसके अलावा, अक्सर चेक्ड पेपर पर एक त्रिकोण के क्षेत्र को खोजने के लिए आवश्यक है।
इस मामले में, आंकड़े के एक तरफ की ऊंचाई को खींचना सबसे सुविधाजनक है, कोशिकाओं द्वारा इसकी लंबाई निर्धारित करें और क्षेत्र को खोजने के लिए सार्वभौमिक सूत्र का उपयोग करें:
एस = A * ए * एच।
इसलिए, लेख में प्रस्तुत सूत्रों का अध्ययन करने के बाद, आपको किसी भी प्रकार के त्रिकोण के क्षेत्र को खोजने में समस्या नहीं होगी।


























