
解決するためのいくつかの基本的なアルゴリズムがあります配列ソートタスク。これらの中で最も有名なものの1つは挿入ソートです。その明快さと単純さのために、しかし効率が低いので、この方法は主にプログラミングを教えるのに使われます。これにより、基本的な並べ替えメカニズムを理解できます。
挿入ソートアルゴリズムの本質は希望する方法で順序付けられたセグメントが元の配列内に形成されるという事実。各要素は、テストされたパーツと1つずつ比較され、適切な場所に挿入されます。したがって、すべての要素を通過した後、それらは正しい順序で並べられます。
要素の選択順序は、次のいずれかになります。それらは任意に、または何らかのアルゴリズムに従って選択できます。ほとんどの場合、配列の先頭からの順次列挙が使用され、順序付けられたセグメントが形成されます。
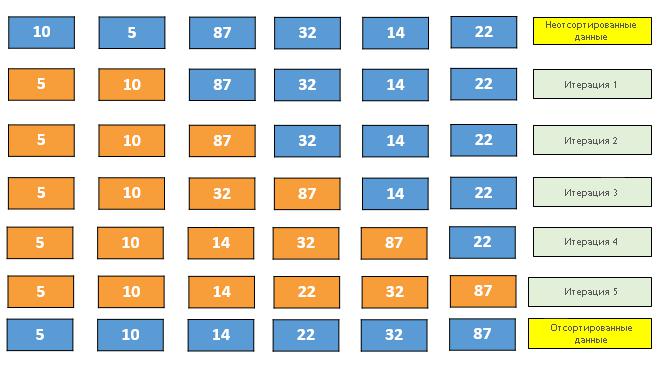
並べ替えの開始は次のようになります。
以下同様に、元の配列の最後まで続きます。
明確にするために、このソートメカニズムが日常生活でどのように使用されているかの例を示す価値があります。
財布を例にとってみましょう。紙幣コンパートメントでは、数百、500、1000番目の紙幣が散らかっています。これは混乱です。そのような混乱の中で、適切な紙をすぐに見つけることは困難です。請求書の配列を並べ替える必要があります。
最初は1000ルーブルの紙幣で、その直後は100です。100を取り、前に置きます。 3番目の列は500ルーブルで、彼女にとって正当な場所は100から1000の間です。
同様に、「フール」をプレイするときに結果のカードを並べ替えて、ナビゲートしやすくします。

挿入ソートメソッドは入力として受け取ります順序付けする元の配列、比較関数、および必要に応じて、要素を列挙するためのルールを定義する関数。ほとんどの場合、代わりに通常のループ演算子が使用されます。
最初の要素はそれ自体が順序集合であるため、比較は2番目の要素から始まります。
アルゴリズムは多くの場合、ヘルパー関数を使用して2つの値を交換します(swap)。追加の一時変数を使用します。これはメモリを大量に消費し、コードの速度をわずかに低下させます。
別の方法は、グループの質量オフセットです。要素とそれに続く空いたスペースへの現在の要素の挿入。この場合、次の要素への遷移は、比較が正しい順序を示す肯定的な結果を返したときに発生します。

具体的な実装は、使用するプログラミング言語、その構文、および構造に大きく依存します。
一時変数を使用して値を交換する従来のC実装:
int i、j、temp; for(i = 1; i <サイズ; i ++) {{ temp =配列[i]; for(j = i-1; j> = 0; j--) {{ if(array [j] <temp) ブレーク; 配列[j + 1] =配列[j]; 配列[j] = temp; } }PHPの実装:
関数挿入ソート(&$ a){ for($ i = 1; $ i <count($ a); $ i ++){ $ x = $ a [$ i]; for($ j = $ i --1; $ j> = 0 && $ a [$ j]> $ x; $ j-){ $ a [$ j + 1] = $ a [$ j]; } $ a [$ j + 1] = $ x; } }ここでは、最初に、並べ替え条件を満たさないすべての要素が右にシフトされ、次に現在の要素が解放されたスペースに挿入されます。
whileループを使用するJavaコード:
public static void insertSort(int [] arr){{ for(int i = 1; i <arr.length; i ++){ int currElem = arr [i]; int prevKey = i-1; while(prevKey> = 0 && arr [prevKey]> currElem){ arr [prevKey + 1] = arr [prevKey]; arr [prevKey] = currElem; prevKey--; } } }コードの一般的な意味は変わりません。配列の各要素は前の要素と順番に比較され、必要に応じてそれらと交換されます。
明らかに、最良の場合、入り口でアルゴリズムのは、すでに正しい方法で順序付けられた配列になります。この状況では、アルゴリズムは単に各要素をチェックして、交換を実行せずにその場所にあることを確認する必要があります。したがって、実行時間は元のO(n)配列の長さに直接依存します。
最悪の場合の入力データは配列であり、逆の順序でソートされます。これには多数の順列が必要になり、ランタイム関数は2乗された要素の数に依存します。
完全に順序付けられていない配列の順列の正確な数は、次の式を使用して計算できます。
n *(n-1)/ 2、ここで、nは元の配列の長さです。したがって、100個の要素を正しい順序で配置するには、4950個の順列が必要です。
挿入方法は、小さい配列または半順序配列をソートするのに非常に効率的です。ただし、計算が非常に複雑であるため、広く使用することはお勧めしません。
このアルゴリズムは、他の多くのより複雑なソート方法のヘルパーとして使用されます。

挿入アルゴリズムは、いわゆる安定したソート。これは、同じ要素を交換するのではなく、元の順序を保持することを意味します。多くの場合、安定性指数は正しい順序付けにとって重要です。

上記は、ダンス挿入ソートの優れた視覚的な例です。
