
19 세기 초 베를린 지오 미터 Jacob Steiner세 마을을 연결하는 작업을 설정하여 길이가 가장 짧아 지도록합니다. 그 후 그는이 문제를 일반화했습니다. 평면에서 한 점을 찾아서 n 개의 다른 점까지의 거리가 가장 작아야합니다. 20 세기에도이 주제에 대한 작업이 계속되었습니다. 여러 지점을 가져 와서 그들 사이의 거리가 가장 짧도록 연결하기로 결정했습니다. 이 모든 것이 연구중인 문제의 특별한 경우입니다.
Kruskal의 알고리즘은 "욕심 많은"알고리즘에 속합니다.(그래디언트라고도 함). 그 본질은 모든 단계에서 가장 큰 성과입니다. 항상 "욕심 많은"알고리즘이 문제에 대한 최상의 솔루션을 제공하는 것은 아닙니다. 특정 문제에 적용하면 최적의 솔루션을 제공한다는 이론이 있습니다. 이것이 마트 로이드 이론입니다. Kruskal의 알고리즘은 이러한 문제에 속합니다.
고려 된 알고리즘은 최적의와이어 프레임 그래프. 이에 대한 문제는 다음과 같습니다. 다중 간선과 루프가없는 무 방향 그래프가 제공되고 간선 집합에 가중치 함수 w가 주어지며, 각 간선 e에 숫자-간선의 가중치-w (e)를 할당합니다. 간선 집합의 각 하위 집합 가중치는 간선 가중치의 합에 의해 결정됩니다. 가장 가벼운 프레임을 찾아야합니다.
Kruskal의 알고리즘은 이와 같이 작동합니다. 먼저 원래 그래프의 모든 모서리가 가중치의 오름차순으로 정렬됩니다. 처음에는 뼈대에 모서리가 포함되어 있지 않지만 그래프의 모든 정점이 포함됩니다. 알고리즘의 다음 단계 후에는 스패닝 포리스트 인 스켈레톤의 이미 구성된 부분에 하나의 가장자리가 추가됩니다. 무작위로 선택되지 않습니다. 와이어 프레임에 속하지 않는 그래프의 모든 모서리를 빨간색 및 녹색이라고 할 수 있습니다. 각 빨간색 가장자리의 정점은 건설중인 숲의 동일한 연결 구성 요소에 있으며 녹색 가장자리의 정점은 서로 다른 정점에 있습니다. 따라서 여기에 빨간색 가장자리를 추가하면주기가 나타나고 녹색이면이 단계 후에 얻은 포리스트의 연결 구성 요소가 하나 줄어 듭니다. 따라서 결과물에 빨간색 가장자리를 추가 할 수 없지만 숲을 만들기 위해 녹색 가장자리를 추가 할 수 있습니다. 그리고 최소한의 무게로 녹색 가장자리가 추가됩니다. 결과는 가장 가벼운 프레임입니다.
현재 숲 F를 표시합시다. 그래프의 정점 세트를 연결 영역으로 분할합니다 (결합은 F를 형성하며 쌍으로 교차하지 않음). 빨간색 가장자리에는 같은 부분에 두 정점이 있습니다. 부분 (x)는 각 꼭지점 x에 대해 x가 속한 부분의 이름을 반환하는 함수입니다. Unite (x, y)는 x 및 y 부분과 다른 모든 부분의 합집합으로 구성된 새 파티션을 만드는 절차입니다. n을 그래프의 간선 수라고합니다. 이 모든 개념은 Kruskal의 알고리즘에 포함되어 있습니다. 이행:
가중치의 오름차순으로 그래프의 모든 모서리를 1 번째부터 n 번째까지 정렬합니다. (ai, bi는 번호가 매겨진 가장자리의 꼭지점입니다).
for i = 1 to n do.
x : = 부품 (ai).
y : = 부분 (bi).
x가 y와 같지 않으면 Unite (x, y), F에 모서리 i를 포함합니다.
T는 Kruskal 알고리즘을 사용하여 구성된 원래 그래프의 골격이고 S는 임의의 골격입니다. w (T)가 w (S)를 초과하지 않는다는 것을 증명해야합니다.
M을 모서리 세트 S, P를 모서리 세트라고 가정합니다.T. S가 T와 같지 않으면 S에 속하지 않는 프레임 T의 가장자리 et가 있습니다. et를 S에 결합합시다.주기가 형성되고이를 C라고합시다. 우리는 C에서 S에 속하는 가장자리 es를 제거합니다. 가장자리는 새 프레임을 얻습니다. 그 안에 많은 봉우리가 있습니다. W (et)는 Kruskal 알고리즘으로 인해 w (es) 이하이기 때문에 가중치는 w (S)를 초과하지 않습니다. T를 얻을 때까지이 작업을 반복합니다 (가장자리 S를 가장자리 T로 대체). 각 후속 결과 프레임의 가중치는 이전 프레임의 가중치보다 크지 않으며 w (T)가 w (S)보다 크지 않습니다.
또한 Kruskal 알고리즘의 정확성은 matroids에 대한 Rado-Edmonds 정리를 따릅니다.
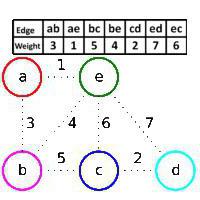
꼭지점 a, b, c, d, e 및 간선 (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). 리브 무게는 표와 그림에 나와 있습니다. 처음에 건설중인 포리스트 F에는 그래프의 모든 정점이 포함되며 가장자리는 포함되지 않습니다. Kruskal의 알고리즘은 가중치가 가장 작고 정점 a와 e가 포리스트 F (가장자리 (a, e)가 녹색 임)의 서로 다른 연결된 구성 요소에 있으므로 가장자리 (a, e)를 먼저 추가 한 다음 가장자리 (c, d)를 추가합니다. 이 모서리가 F에 속하지 않는 그래프 모서리의 가중치가 가장 적고 녹색이면 동일한 이유로 모서리 (a, b)가 추가됩니다. 그러나 가장자리 (b, e)는 빨간색이기 때문에 나머지 가장자리의 가중치가 가장 작더라도 건너 뜁니다. 꼭지점 b와 e는 포리스트 F의 동일한 연결된 구성 요소에 속합니다. 즉, 가장자리 (b, e)를 F에 추가하면 주기. 그런 다음 녹색 가장자리 (b, c)가 추가되고 빨간색 가장자리 (c, e)가 건너 뛴 다음 d, e가 추가됩니다. 따라서 가장자리 (a, e), (c, d), (a, b), (b, c)가 순차적으로 추가됩니다. 초기 그래프의 최적 골격은 이들로 구성됩니다. 이 경우 알고리즘이 작동하는 방식입니다. 그린. 예가 이것을 보여줍니다.

그림은 두 개의 연결된 구성 요소로 구성된 그래프를 보여줍니다. 굵은 선은 Kruskal 알고리즘을 사용하여 구축 된 최적 골격 (녹색)의 가장자리를 나타냅니다.

위 그림은 원래 그래프를 보여주고 아래 그림은 고려 된 알고리즘을 사용하여 구성된 최소 가중치 골격을 보여줍니다.
추가 된 모서리의 순서 : (1,6); (0.3), (2.6) 또는 (2.6), (0.3)-중요하지 않습니다. (3.4); (0.1), (1.6) 또는 (1.6), (0.1)도 무관심합니다 (5.6).

Kruskal의 알고리즘은 예를 들어 통신 배치, 각 국가의 새로운 정착지의 도로 및 기타 경우를 최적화하기위한 실용적인 응용 프로그램을 찾습니다.
