Įterpti rūšiavimą: pavyzdžiai, kaip veikia algoritmas

Yra keletas pagrindinių sprendimų algoritmųmasyvo rūšiavimo užduotys. Vienas garsiausių iš jų yra įdėklų rūšiavimas. Dėl aiškumo ir paprastumo, tačiau mažas efektyvumas, šis metodas daugiausia naudojamas mokymo programavimui. Tai leidžia suvokti pagrindinius rūšiavimo mechanizmus.

Algoritmo apibūdinimas

Rūšiavimo algoritmo esmė yraTas faktas, kad pradiniame masyve užsakytas segmentas formuojamas teisingai. Kiekvienas elementas yra lyginamas po vieną su patikrinta dalimi ir įdėtas į tinkamą vietą. Taigi, ieškodami visų elementų, jie yra išdėstyti teisinga tvarka.

Elementų atrankos tvarka gali būti bet kuri,juos galima pasirinkti savavališkai arba pagal tam tikrą algoritmą. Dažniausiai serijinė paieška naudojama nuo masyvo pradžios, kuriame formuojamas užsakytas segmentas.

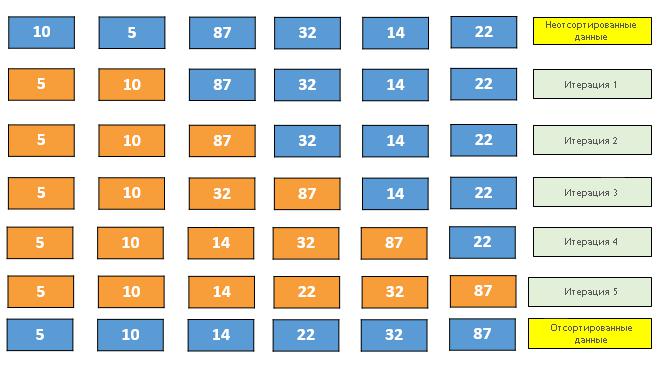
Rūšiavimo pradžia gali atrodyti taip:

1. Paimkite pirmąjį masyvo elementą.
2. Kadangi nėra palyginimo, paimkite elementą kaip užsakytą seką.
3. Eikite į antrąjį elementą.
4. Palyginkite jį su pirmuoju pagal rūšiavimo taisyklę.
5. Jei reikia, pakeiskite elementus vietose.
6. Priimkite pirmuosius du užsakytos sekos elementus.
7. Eikite į trečiąjį elementą.
8. Palyginkite jį su antrąja, jei reikia, apsikeitimo teise.
9. Jei pakeičiamas, palyginkite jį su pirmuoju.
10. Paimkite tris elementus pagal užsakytą seka.

Ir taip iki pradinio masyvo pabaigos.

Rūšiavimo įdėklai realiame gyvenime

Siekiant aiškumo, verta pateikti pavyzdį, kaip šis rūšiavimo mechanizmas naudojamas įprastu gyvenimu.

Paimkite, pavyzdžiui, piniginę.Banknotų skyriuje yra šimtai penkis šimtus tūkstančių užrašų. Tai netvarka, tokiu atveju sunku iš karto rasti tinkamą popierių. Sąskaitų masė turi būti rūšiuojama.

Pirmasis yra banknotas nominalios vertės 1000 rublių, o iš karto po jo - 100. Priimame šimtą ir padėkite jį į priekį. Trečias iš eilės yra 500 rublių, jo teisėta vieta yra nuo šimto tūkstančio.

Tuo pačiu būdu mes rūšiame gaunamas korteles, kai žaidžiame "Fool", kad būtų lengviau jas naršyti.

Operatoriai ir pagalbinės funkcijos

Įterpiklių rūšiavimo metodas įvedamasnurodomas šaltinio masyvas, palyginimo funkcija ir, jei reikia, funkcija, apibrėžianti elementų sąrašo taisyklę. Dažniausiai naudojamas įprastas kilpos operatorius.

Pirmasis elementas yra užsakytas rinkinys, todėl palyginimas prasideda nuo antrojo.

Algoritmas dažnai naudoja pagalbinę funkciją, norint keistis dviem vertėmis (apsikeitimo). Jis naudoja papildomą laikiną kintamąjį, kuris reikalauja atminties ir šiek tiek sulėtino kodą.

Alternatyva yra grupės masės poslinkis.elementai ir vėlesnis įterpimas į laisvą erdvę. Šiuo atveju perėjimas prie kito elemento atsiranda tada, kai lyginimas duoda teigiamą rezultatą, kuris rodo teisingą tvarką.

Įgyvendinimo pavyzdžiai

Konkretus įgyvendinimas labai priklauso nuo naudojamos programavimo kalbos, jos sintaksės ir struktūros.

Klasikinis diegimas C naudojant laikiną kintamųjų vertę:

int i, j, temp;
už (i = 1; i  = 0; j--)
{
jei (masyvas [j] 

PHP diegimas:

funkcija insertion_sort (& $ a) {
už ($ i = 1; $ i  = 0 & & $ a [$ j]> $ x; $ j--) {
$ a [$ j + 1] = $ a [$ j];
}
$ a [$ j + 1] = $ x;
}
}

Čia pirmiausia visi elementai, neatitinkantys rūšiavimo sąlygos, perkeliami į dešinę, o tada dabartinis elementas įterpiamas į atlaisvintą vietą.

„Java“ kodas naudojant „loop“:

viešas statinis negaliojantis įterpimasSortas (int [] arr){
už (int i = 1; i  = 0 && arr [prevKey]> currElem) {
arr [prevKey + 1] = arr [prevKey];
arr [prevKey] = currElem;
prevKey--;
}
}
}

Bendroji kodo reikšmė lieka tokia pati: kiekvienas masyvo elementas yra nuosekliai lyginamas su ankstesniais elementais ir prireikus keičia vietas su jais.

Darbo laiko vertinimas

Очевидно, что в самом лучшем случае на входе Algoritmas bus jau užsakyta masyvas. Esant tokiai situacijai, algoritmas paprasčiausiai turės patikrinti kiekvieną elementą, kad įsitikintų, jog jis yra jo vietoje, nesikeisdamas mainais. Taigi, veikimo laikas tiesiogiai priklauso nuo pradinio O (n) masyvo ilgio.

Blogiausio atvejo įvesties duomenys yra masyvas,rūšiuojami atvirkštine tvarka. Tam reikės daugybės permutacijų, vykdymo laiko funkcija priklausys nuo kvadratų sudarytų elementų skaičiaus.

Tikslų visiškai nesutvarkyto masyvo permutacijų skaičių galima apskaičiuoti pagal formulę:

n * (n-1) / 2

, kur n yra pradinio masyvo ilgis. Taigi, norint 100 elementų išdėstyti teisinga tvarka, reikia 4950 permutacijų.

Įterpimo būdas yra labai efektyvus rūšiuojant mažus arba dalinai sutvarkytus masyvus. Tačiau plačiai naudoti nerekomenduojama dėl didelio skaičiavimų sudėtingumo.

Algoritmas naudojamas kaip pagalbininkas daugelyje kitų sudėtingesnių rūšiavimo metodų.

Rūšiuojant tas pačias vertes

Įterpimo algoritmas priklauso vadinamajamstabilios rūšys. Tai reiškia, kad jis nekeičia identiškų elementų, bet išsaugo jų pradinę tvarką. Stabilumo indeksas daugeliu atvejų yra svarbus teisingam užsakymui.

Aukščiau pateiktas puikus vaizdinis šokio įterpimo rūšies pavyzdys.