
Trikampis yra vienas iš labiausiai paplitusiųgeometrines figūras, su kuriomis mes esame pažįstami pradinėje mokykloje. Klausimas, kaip rasti trikampio plotą, kiekvienas studentas susiduria geometrijos pamokose. Taigi, kokios yra šio skaičiaus srities nustatymo ypatybės? Šiame straipsnyje apžvelgsime pagrindines šios užduoties formules, taip pat analizuosime trikampių tipus.

Trikampio plotą galite rasti visiškai skirtingais būdais, nes geometrijoje yra daugiau nei vienos rūšies formos, kurioje yra trys kampai. Šios rūšys yra:
Pažvelkime atidžiau į kiekvieną iš esamų tipų trikampius.

Tokia geometrinė forma laikoma labiausiaiįprasta sprendžiant geometrines problemas. Kai atsiranda poreikis atkreipti savavališką trikampį, tai yra ta galimybė, kuri ateina į gelbėjimą.
Ūminiame trikampyje, kaip rodo pavadinimas, visi kampai yra aštrūs ir prideda iki 180 °.
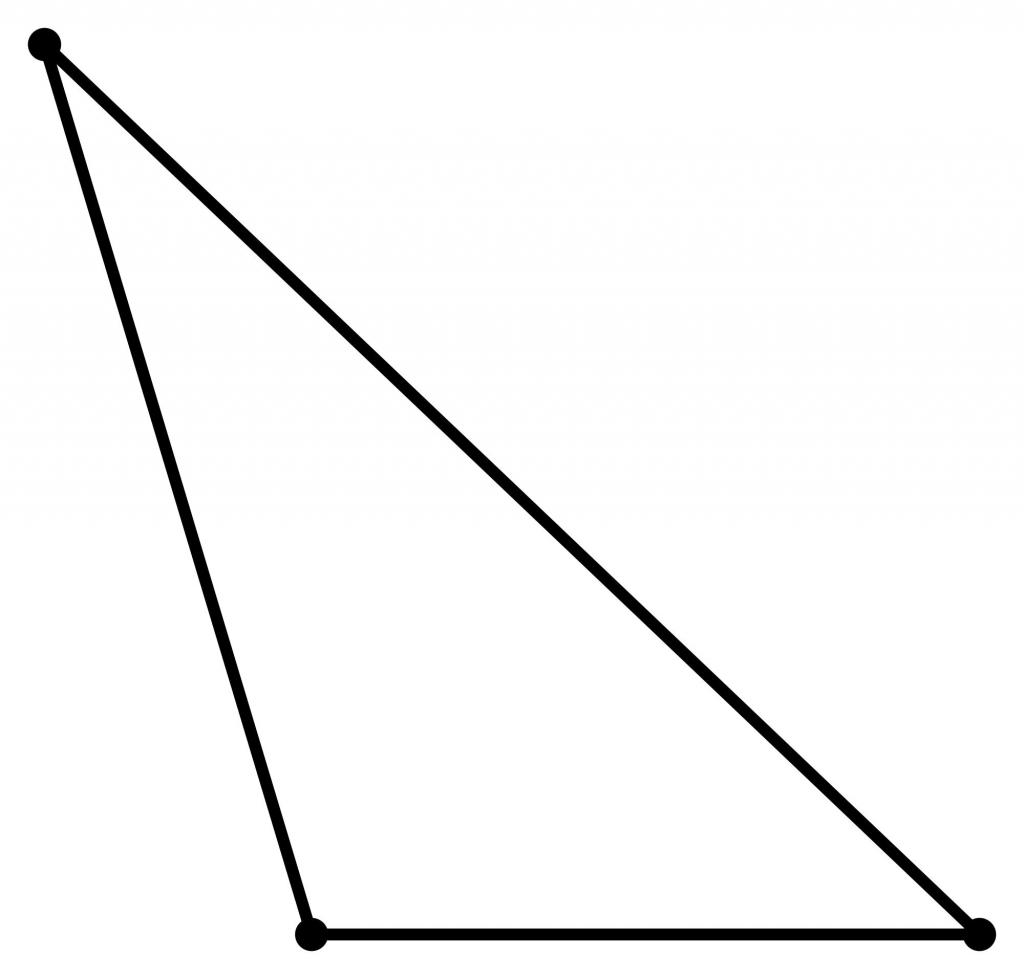
Такой треугольник также очень распространен, tačiau jis rečiau aptinkamas smailiu kampu. Pvz., Spręsdami trikampius (tai yra, žinote keletą jo kraštų ir kampų ir jums reikia rasti likusius elementus), kartais reikia nustatyti, ar kampas yra neryškus. Neįprasto kampo kosinusas yra neigiamas skaičius.
Nerūdijančio kampo trikampyje vieno iš kampų dydis viršija 90 °, taigi likusieji du kampai gali būti nedideli (pvz., 15 ° arba 3 °).
Norėdami rasti tokio tipo trikampio plotą, turite žinoti kai kuriuos niuansus, kuriuos aptarsime toliau.
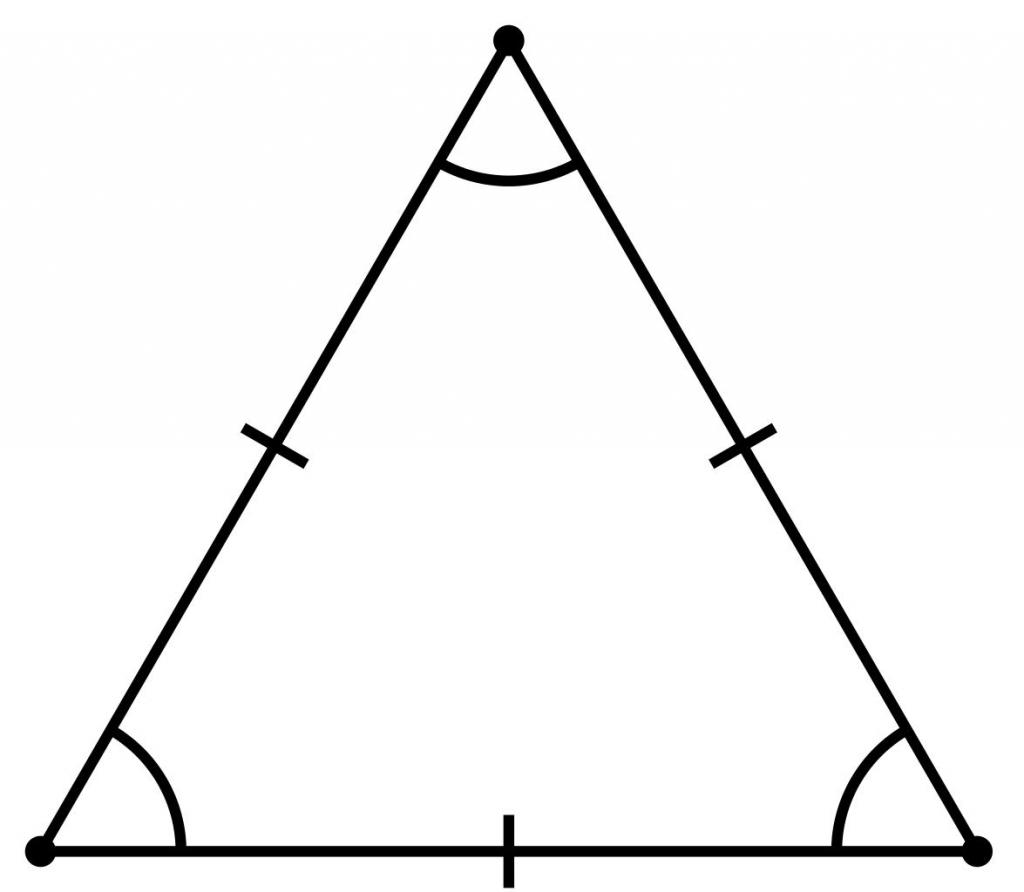
Įprastas daugiakampis yra figūraįskaitant n kampus, kuriuose visos kraštinės ir kampai yra lygūs. Tai taisyklingas trikampis. Kadangi visų trikampio kampų suma yra 180 °, kiekvienas iš trijų kampų yra 60 °.
Taisyklingas trikampis dėl savo savybės dar vadinamas lygiakraščiu skaičiumi.
Taip pat verta paminėti, kad į taisyklingą trikampį galima įrašyti tik vieną apskritimą, o aplink jį galima apibūdinti tik vieną apskritimą, o jų centrai yra viename taške.

Be lygiakraščio tipo, taip pat galima išskirtilygiašonis trikampis, šiek tiek skiriasi nuo jo. Tokiame trikampyje dvi pusės ir du kampai yra lygūs vienas kitam, o trečioji pusė (prie kurios lygi kampai yra greta) yra pagrindas.
Paveikslėlyje pavaizduotas lygiašonis trikampis DEF, kurio kampai D ir F yra lygūs, o DF yra pagrindas.

Stačiakampis trikampis taip pavadintas, nes vienas jo kampų yra tiesus, tai yra, jis lygus 90 °. Kiti du kampai padidėja iki 90 °.
Didžiausia tokio trikampio pusė, esanti priešinga 90 ° kampu, yra hipotenuzė, o kitos dvi jo pusės yra kojos. Šio tipo trikampiams taikoma Pitagoro teorema:
Kojų ilgių kvadratų suma yra lygi hipotenuzės ilgio kvadratui.
Paveikslėlyje pavaizduotas stačiakampis trikampis BAC su hipotenuzu AC ir kojomis AB ir BC.
Norėdami rasti trikampio su stačiu kampu plotą, turite žinoti jo kojų skaitines reikšmes.
Pereikime prie formulių, kaip rasti šio paveikslo plotą.
В геометрии можно выделить две формулы, которые tinka rasti daugumos tipų trikampių plotą, būtent stačiakampius, pailgus, taisyklingus ir lygiašonius trikampius. Paanalizuokime kiekvieną iš jų.
Ši formulė yra universaliradę figūros plotą, į kurį svarstome. Norėdami tai padaryti, pakanka žinoti šono ilgį ir į jį atkreipto aukščio ilgį. Pati formulė (pusė produkto sandaugos ir aukščio) yra tokia:
S = ½ * A * H,
kur A yra nurodyto trikampio kraštinė, o H yra trikampio aukštis.

Pvz., Norėdami rasti aštriojo trikampio ACB plotą, padauginkite jo kraštinę AB iš aukščio CD ir gautą vertę padalinkite iš dviejų.
Tačiau ne visada lengva rasti teritorijątrikampis tokiu būdu. Pavyzdžiui, norint naudoti šią formulę neryškiam trikampiui, reikia tęsti vieną iš jo kraštų ir tik tada atkreipti į jį aukštį.
Praktiškai ši formulė naudojama dažniau nei kitos.
Ši formulė, kaip ir ankstesnė, tinkadaugumos trikampių ir savo reikšme yra formulės, kaip rasti plotą pagal trikampio kraštinę ir aukštį, pasekmė. Tai reiškia, kad nagrinėjamą formulę galima lengvai išvesti iš ankstesnės. Jo formuluotė atrodo taip:
S = ½ * sinO * A * B,
kur A ir B yra trikampio kraštinės, o O yra kampas tarp kraštinių A ir B.
Prisiminkite, kad kampo sinusą galima apžiūrėti specialioje lentelėje, pavadintoje iškiliojo sovietinio matematiko V. M. Bradio vardu.
Dabar pereikime prie kitų formulių, tinkančių tik išskirtiniams trikampių tipams.
Be universalios formulės, kuri apima poreikį nubrėžti aukštį trikampyje, jo kojos gali rasti trikampio, kuriame yra stačiu kampu, plotą.
Taigi, trikampio, kuriame yra stačiakampis, plotas yra pusė jo kojų sandaugos arba:
S = ½ * a * b,
kur a ir b yra stačiakampio trikampio kojos.
Šis geometrinių figūrų tipas skiriasi tuokad jo plotą galima rasti tik nurodytai tik vienos jo pusės vertei (nes visos taisyklingo trikampio kraštinės yra lygios). Taigi, susidūrę su problema „raskite trikampio plotą, kai kraštinės yra lygios“, turite naudoti šią formulę:
S = A2* √3 / 4,
kur A yra lygiakraščio trikampio kraštinė.
Paskutinė galimybė rasti trikampio plotą yra Herono formulė. Norėdami juo naudotis, turite žinoti trijų figūros kraštų ilgį. Herono formulė atrodo taip:
S = √p (p - a) (p - b) (p - c),
kur a, b ir c yra šio trikampio kraštinės.
Kartais pateikiama tokia problema:„Taisyklingo trikampio plotas - suraskite jo ilgį“. Tokiu atveju turite naudoti jau žinomą formulę, kad surastumėte taisyklingo trikampio plotą ir iš jo išvestumėte kraštinės (arba jos kvadrato) vertę:
A2 = 4S / √3.
GIA problemose matematikoje yra daug formulių. Be to, ant languoto popieriaus dažnai reikia rasti trikampio plotą.
Tokiu atveju patogiausia nubrėžti aukštį į vieną iš figūros šonų, nustatyti jo ilgį ląstelėmis ir naudoti universalią formulę plotui surasti:
S = ½ * A * H
Taigi, išstudijavę straipsnyje pateiktas formules, jums nekils problemų ieškant bet kokio trikampio ploto.


























