
19. gadsimta sākumā Džeobs Steiners no Berlīnes izveidoja ģeometruuzdevums, kā savienot trīs ciemus, lai to garums būtu visīsākais. Pēc tam viņš vispārināja šo problēmu: ir nepieciešams atrast punktu plaknē, lai attālums no tā līdz n citiem punktiem būtu vismazākais. 20. gadsimtā turpinājās darbs šajā jautājumā. Tika nolemts veikt vairākus punktus un tos savienot tā, lai attālums starp tiem būtu visīsākais. Tas viss ir īpašs pētāmās problēmas gadījums.
Kraskala algoritms ir "mantkārīgs" algoritms(tos sauc arī par gradientu). To būtība - lielākais ieguvums katrā solī. Ne vienmēr "mantkārīgie" algoritmi dod vislabāko risinājumu problēmai. Ir teorija, kas parāda, ka, piemērojot konkrētus uzdevumus, tie nodrošina optimālu risinājumu. Tā ir matroīdu teorija. Kraskala algoritms attiecas uz šādām problēmām.
Aplūkotais algoritms konstruē optimālostieples rāmja grafiks. Problēma par to ir šāda. Jums tiek piešķirts nenovirzīts grafiks bez vairākām malām un cilpām, un uz tā malu kopas tiek dota svara funkcija w, kas katrai malai e piešķir skaitli - malas svaru - w (e). Katras apakškopas svaru no malu kopas nosaka tā malu svaru summa. Nepieciešams atrast rāmi ar mazāko svaru.
Kruskaļa algoritms darbojas šādi. Pirmkārt, visas sākotnējā grafika malas ir sakārtotas svaru augošā secībā. Sākumā skelets nesatur malas, bet ietver visas grafika virsotnes. Pēc nākamā algoritma soļa viena mala tiek pievienota jau uzbūvētajai skeleta daļai, kas ir aptverošs mežs. Tas nav nejauši izvēlēts. Visas diagrammas malas, kas nepieder pie stiepļu rāmja, var saukt par sarkanām un zaļām. Katras sarkanās malas virsotnes atrodas vienā savienotā būvējamā meža komponentā, un zaļās malas virsotnes atrodas dažādās. Tāpēc, ja tur pievienojat sarkanu malu, parādās cikls, un, ja tas ir zaļš, savienojuma komponents mežā, kas iegūts pēc šī soļa, būs par vienu mazāks. Tādējādi iegūtajai konstrukcijai nevar pievienot sarkanu malu, bet meža izveidošanai var pievienot jebkuru zaļo malu. Un tiek pievienota zaļa mala ar minimālo svaru. Rezultāts ir vieglākais rāmis.
Apzīmēsim pašreizējo mežu F. Tas sadala grafa virsotņu kopu savienotos reģionos (to savienojuma formas ir F, un tās nekrustojas pa pāriem). Sarkanajām malām abās virsotnēs ir viena un tā pati daļa. Daļa (x) ir funkcija, kas katram virsotnei atgriež tās daļas nosaukumu, kurai pieder x. Unite (x, y) ir procedūra, kas izveido jaunu nodalījumu, kas sastāv no x un y daļu un visu pārējo daļu savienojuma. Ļaujiet n būt diagrammas malu skaitam. Visi šie jēdzieni ir iekļauti Kruskaļa algoritmā. Īstenošana:
Sakārtojiet visas diagrammas malas no 1. līdz n-tā svara pieaugošā secībā. (ai, bi ir malas i virsotnes).
par i = 1 līdz n darīt.
x: = Daļa (ai).
y: = daļa (bi).
Ja x nav vienāds ar y, tad apvienojiet (x, y), iekļaujiet F malu F.
Ļaujiet T būt sākotnējā grafa skeletam, kas izveidots, izmantojot Kruskala algoritmu, un S tā patvaļīgajam skeletam. Mums jāpierāda, ka w (T) nepārsniedz w (S).
Lai M ir malu kopa S, P ir malu kopaT. Ja S nav vienāds ar T, tad ir rāmja T mala et, kas nepieder S. Pievienosimies et S. Tiek izveidots cikls, sauksim to par C. Mēs noņemam no C visas S. piederošās malas. un tajā ir tikpat daudz virsotņu. Tā svars nepārsniedz w (S), jo Kruskala algoritma dēļ w (et) ir ne vairāk kā w (es). Mēs atkārtosim šo darbību (nomainot malas S ar malām T), līdz iegūstam T. Katra nākamā iegūtā rāmja svars nav lielāks par iepriekšējā rāmja svaru, no kā izriet, ka w (T) nav lielāks par w (S).
Arī Kruskala algoritma pareizība izriet no Rado-Edmonds teorēmas par matroīdiem.
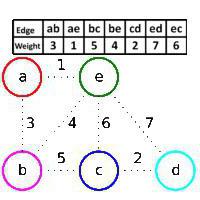
Grafiks ar virsotnēm a, b, c, d, e un malām (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Ribu svars ir parādīts tabulā un attēlā. Sākotnēji būvējamais mežs F satur visas diagrammas virsotnes un nesatur malas. Kruskaļa algoritms vispirms pievieno malu (a, e), jo tam ir mazākais svars, un virsotnes a un e atrodas dažādos savienotos meža F komponentos (mala (a, e) ir zaļa), tad malu (c, d), tāpēc ka šai malai ir vismazākais grafa malu svars, kas nepieder pie F, un tā ir zaļa, tad malu (a, b) pievieno to pašu iemeslu dēļ. Bet mala (b, e) tiek izlaista, kaut arī tai ir mazākais atlikušo malu svars, jo tā ir sarkana: virsotnes b un e pieder pie tā paša savienotā meža F komponenta, tas ir, ja mēs pievienojam malu (b, e) F, tas veido cikls. Tad pievieno zaļu malu (b, c), izlaiž sarkanu malu (c, e) un pēc tam d, e. Tādējādi malas (a, e), (c, d), (a, b), (b, c) tiek pievienotas secīgi. Sākotnējā grafika optimālais skelets sastāv no tiem. Šajā gadījumā algoritms darbojas šādi Krāsots. Piemērs to parādīja.

Attēlā parādīts grafiks, kas sastāv no diviem savienotiem komponentiem. Treknrakstā redzamās līnijas parāda optimālā stieples rāmja (zaļā) malas, kas izveidotas, izmantojot Kruskal algoritmu.

Augšējā attēlā parādīts sākotnējais grafiks, bet apakšējā - minimālais svara skelets, kas tam uzbūvēts, izmantojot aplūkoto algoritmu.
Pievienoto malu secība: (1,6); (0,3), (2,6) vai (2,6), (0,3) - nav nozīmes; (3.4); (0,1), (1,6) vai (1,6), (0,1) ir arī vienaldzīgs (5,6).

Kruskala algoritms atrod praktisku pielietojumu, piemēram, lai optimizētu komunikāciju, ceļu ierīkošanu katras valsts apdzīvoto vietu jaunajos mikrorajonos, kā arī citos gadījumos.


























