
Ikviens, kurš kādreiz ir domājisLai kļūtu par IT speciālistu vai sistēmas administratoru un vienkārši savienotu likteni ar datortehnoloģijām, ir absolūti nepieciešamas zināšanas par to, kā skaitļi tiek attēloti datora atmiņā. Galu galā tieši uz tā balstās zema līmeņa programmēšanas valodas, piemēram, Assembler. Tāpēc šodien mēs apsvērsim skaitļu attēlojumu datorā un to izvietojumu atmiņas šūnās.

Ja jūs lasāt šo rakstu, tad, visticamākpar to jau zina, bet ir vērts atkārtot. Visi personālā datora dati tiek glabāti bināro skaitļu sistēmā. Tas nozīmē, ka jebkuram skaitlim jābūt attēlotam atbilstošā formā, tas ir, sastāv no nullēm un tām.
Lai tulkotu parastos decimālos skaitļus datorā saprotamā formā, jums jāizmanto tālāk aprakstītais algoritms. Ir arī specializēti kalkulatori.
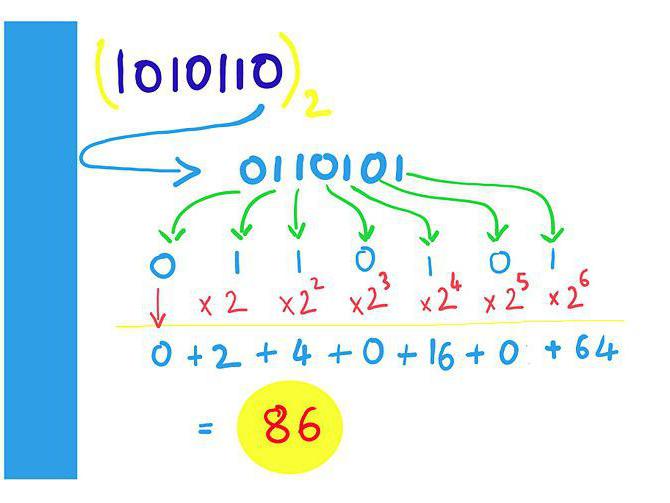
Tātad, lai skaitli pārveidotu par bināruskaitļu sistēmā, jums jāņem izvēlētā vērtība un jāsadala ar 2. Pēc tam mēs iegūstam rezultātu un atlikušo daļu (0 vai 1). Atkārtoti sadaliet rezultātu 2 un atcerieties atlikušo daļu. Šī procedūra jāatkārto, līdz beigās ir arī 0 vai 1. Tad gala vērtību un atlikumus pierakstām apgrieztā secībā, kā mēs tos saņēmām.
Tādā veidā notiek skaitļu attēlojums datorā. Jebkurš skaitlis tiek uzrakstīts binārā formā un pēc tam aizņem atmiņas šūnu.

Kā jums jau vajadzētu zināt, minimālaisinformācijas vienība ir 1 bits. Kā mēs jau noskaidrojām, skaitļu attēlojums datorā notiek binārā formātā. Tādējādi katru atmiņas bitu aizņem viena vērtība - 1 vai 0.
Šūnas tiek izmantotas liela skaita saglabāšanai.Katra šāda vienība satur līdz 8 bitiem informācijas. Tāpēc mēs varam secināt, ka minimālā vērtība katrā atmiņas segmentā var būt 1 baits vai būt astoņciparu binārs skaitlis.
Visbeidzot mēs nonācām pie tiešas datu izvietošanas datorā. Kā jau minēts, procesors vispirms pārtulko informāciju binārā formātā un tikai pēc tam ievieto to atmiņā.
Mēs sāksim ar vienkāršāko variantu, ar kuruir veselu skaitļu attēlojums datorā. Datora atmiņa šim procesam piešķir smieklīgi mazu šūnu skaitu - tikai vienu. Tādējādi vienā slotā maksimums var būt vērtības no 0 līdz 11111111. Pārvērsim maksimālo skaitu parastajā apzīmējumu formā.
X = 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 1 × 28 - 1 = 255.
Tagad mēs redzam, ka vienā atmiņas šūnā vardiapazons no 0 līdz 255. Tomēr tas attiecas tikai uz veseliem skaitļiem, kas nav negatīvi. Ja datoram ir jāpieraksta negatīva vērtība, viss notiks mazliet savādāk.

Tagad redzēsim, kā tas notiksskaitļu attēlojums datorā, ja tie ir negatīvi. Lai uzņemtu vērtību, kas ir mazāka par nulli, tiek piešķirtas divas atmiņas šūnas vai 16 informācijas biti. Šajā gadījumā 15 iet zem paša numura, un pirmais (kreisākais) bits ir norādīts zem attiecīgās zīmes.
Ja cipars ir negatīvs, tad rakstiet "1", ja pozitīvs, tad "0". Iegaumēšanas ērtībai varat uzzīmēt šādu līdzību: ja ir zīme, tad ielieciet 1, ja tā nav, tad neko (0).
Pārējie 15 informācijas biti tiek piešķirti skaitlim.Līdzīgi kā iepriekšējā gadījumā, tajos var ievietot ne vairāk kā piecpadsmit vienības. Ir vērts atzīmēt, ka negatīvo un pozitīvo skaitļu reģistrēšana ievērojami atšķiras viens no otra.
Lai ietilptu 2 atmiņas vietāsvērtība ir lielāka vai vienāda ar nulli, tiek izmantots tā sauktais tiešais kods. Šī darbība tiek veikta tāpat kā aprakstīts, un maksimālais A = 32766, ja izmantojat decimālo skaitļu sistēmu. Es gribētu uzreiz atzīmēt, ka šajā gadījumā "0" attiecas uz pozitīvajiem.
Veselu skaitļu attēlojums datora atmiņā navir tik grūts uzdevums. Tomēr tas kļūst nedaudz sarežģītāk, ja runa ir par negatīvām vērtībām. Lai uzrakstītu skaitli, kas ir mazāks par nulli, tiek izmantots papildu kods.
Lai to iegūtu, iekārta veic vairākas palīgdarbības.
Sniegsim ilustratīvu piemēru.Pieņemsim, ka mums ir skaitlis X = - 131. Pirmkārt, mēs iegūstam tā moduli | X | = 131. Tad mēs to pārtulkojam binārā sistēmā un ierakstām 16 šūnās. Mēs iegūstam X = 0000000010000011. Pēc apgriešanas X = 1111111101111100. Pievienojiet tam "1" un iegūstiet reverso kodu X = 1111111101111101. Lai rakstītu uz 16 bitu atmiņas šūnu, minimālais skaits ir X = - (215) = - 32767.
Kā redzat, reālo skaitļu attēlojumsdators nav tik grūts. Tomēr šis diapazons var nebūt pietiekams lielākajai daļai darbību. Tāpēc, lai uzņemtu lielu skaitu, dators no atmiņas piešķir 4 šūnas jeb 32 bitus.
Ierakstīšanas process vispār neatšķiras no iepriekš aprakstītā. Tātad mēs tikai uzskaitīsim to numuru diapazonu, kurus var saglabāt šajā tipā.
Xšūpoles= 2 147 483 647.
Xmin= - 2 147 483 648.

Vairumā gadījumu šīs vērtības ir pietiekamas, lai reģistrētu un veiktu datu darbības.
Reālo skaitļu attēlojums datorāir priekšrocības un trūkumi. No vienas puses, šī tehnika atvieglo darbību veikšanu starp veselu skaitļu vērtībām, kas ievērojami paātrina procesoru. No otras puses, šis diapazons nav pietiekams, lai atrisinātu lielāko daļu problēmu ekonomikā, fizikā, aritmētikā un citās zinātnēs. Tāpēc tagad mēs apsvērsim citu supervalūtu tehniku.
Šī ir pēdējā lieta, par kuru jums jāzinaskaitļu attēlojums datorā. Tā kā, rakstot frakcijas, rodas problēma noteikt komatu stāvokli tajos, dators šādu skaitļu izvietošanai izmanto eksponenciālu formu.
Jebkuru skaitli var attēlot šādā formā X = m * pn... Kur m ir skaitļa mantissa, p ir skaitļu sistēmas pamats, un n ir skaitļa secība.
Standartizējot peldošo punktu skaitļu reģistrēšanu, tiek izmantots šāds nosacījums, saskaņā ar kuru mantisas modulim jābūt lielākam vai vienādam ar 1 / n un mazākam par 1.
Dosim mums numuru 666,66. Pārejam to uz eksponenciālo formu. Izrādās, X = 0.66666 * 103... P = 10 un n = 3.
Peldošā komata vērtības parasti tiek saglabātas 4 vai 8 baitos (32 vai 64 biti). Pirmajā gadījumā to sauc par parasto precizitātes skaitli, bet otrajā - par dubulto precizitāti.
No 4 baitiem, kas piešķirti ciparu glabāšanai, 1 (8biti) tiek dots datiem par pasūtījumu un tā zīmi, un 3 baiti (24 biti) tiek izmantoti, lai uzglabātu mantisu un tās zīmi saskaņā ar tiem pašiem principiem kā veselu skaitļu vērtībām. Zinot to, mēs varam veikt vienkāršus aprēķinus.
Maksimālā vērtība n = 11111112 = 12710... Pamatojoties uz to, mēs varam iegūt maksimālo skaitļa lielumu, ko var saglabāt datora atmiņā. X = 2127... Tagad mēs varam aprēķināt maksimāli iespējamo mantisu. Tas būs vienāds ar 223 - 1 ≥ 223 = 2(10 × 2,3) ≥ 10002,3 = 10(3 × 2,3) ≥ 107... Rezultātā mēs saņēmām aptuveno vērtību.
Ja mēs tagad apvienojam abus aprēķinus, iegūstam vērtību, kuru var ierakstīt bez zaudējumiem 4 baitu atmiņā. Tas būs vienāds ar X = 1,701411 * 1038... Pārējie skaitļi tika izmesti, jo tieši šo precizitāti pieļauj šī ierakstīšanas metode.

Tā kā visi aprēķini ir ieplānoti unpaskaidrots iepriekšējā rindkopā, šeit mēs visu izskaidrosim ļoti īsi. Divkāršās precizitātes skaitļiem parasti tiek piešķirti 11 biti pasūtījumam un tā zīmei, kā arī 53 biti mantisai.
P = 11111111112 = 102310.
M = 252 -1 = 2(10 * 5,2) = 10005.2 = 1015.6... Mēs noapaļojam uz augšu un iegūstam maksimālo skaitli X = 21023 precīzi līdz "m".
Mēs ceram, ka mūsu sniegtā informācija par veselu skaitļu un reālo skaitļu attēlojumu datorā jums būs noderīga mācībās un būs vismaz nedaudz skaidrāka nekā tas, kas parasti tiek rakstīts mācību grāmatās.


























