
Leonards Eulers (1707-1783) - slavenais Šveiceun krievu matemātiķis, Sanktpēterburgas Zinātņu akadēmijas loceklis, dzīvoja lielākajā daļā savas dzīves Krievijā. Slavenākais matemātiskajā analīzē, statistikā, datorzinātnēs un loģikā ir Eulera aplis (Euler-Venn diagramma), ko izmanto, lai apzīmētu jēdzienu un elementu kopumu.
John Venn (1834-1923) - angļu filozofs un loģists, Euler-Venn diagrammas līdzautors.
Loģikas jēdziens nozīmē formudomāšana, kas atspoguļo viendabīgu priekšmetu klases būtiskās iezīmes. Tos apzīmē ar vienu vai vairāku vārdu grupu: "pasaules karte", "dominējošais kvinteptiskais akords", "pirmdiena" utt.
Gadījumā, ja viena jēdziena apjoma elementipilnībā vai daļēji pieder pie cita apjoma, viņi runā par saderīgām koncepcijām. Ja neviena konkrēta jēdziena apjoma daļa neietilpst cita apjoma ziņā, mums ir vieta ar nesaderīgām koncepcijām.

Savukārt katram no koncepciju veidiem ir sava iespējamo attiecību kopa. Savietojamām koncepcijām tās ir:
Par nesaderīgu:
Shematiski sakarība starp koncepcijām loģikā parasti tiek apzīmēta ar Euler-Venn aprindu palīdzību.
Šajā gadījumā jēdzieni attiecas uz to pašu tēmu. Attiecīgi šo jēdzienu apjomi ir pilnīgi vienādi. Piemēram:
A - Sigmund Freud;
B - psihoanalīzes dibinātājs.

Vai:
Un - laukums;
B ir taisnstūra taisnstūris;
C - taisnstūra rombs.
Apzīmējumam tiek izmantoti pilnīgi vienādi Eulera apļi.
Šajā kategorijā ietilpst jēdzieni, kuriem ir kopīgi elementi, kas attiecas uz crossover. Tas nozīmē, ka viena no jēdzieniem ir daļēji iekļauts otrajā apjomā:
A - skolotājs;
B ir mūzikas mīļotājs.

Kā redzams šajā piemērā, jēdzienu jomapārklāšanās: atsevišķa skolotāju grupa var būt mūzikas mīļotāji, un otrādi - starp mūzikas mīļotājiem var būt skolotāja profesijas pārstāvji. Līdzīga attieksme būs gadījumā, ja, kā A jēdziens, darbojas, piemēram, “pilsētnieks” un B - “automašīnu vadītājs”.
Shematiski apzīmēts kā atšķirīgs mērogā.Eulera loki. Attiecības starp jēdzieniem šajā gadījumā raksturo tas, ka pakārtotais jēdziens (mazāks apjomā) ir pilnībā iekļauts padotības sastāvā (lielāks apjomā). Šajā gadījumā pakārtotais jēdziens neizplata pilnīgi pakārtoto.
Piemēram:
Koks;
B - priede.
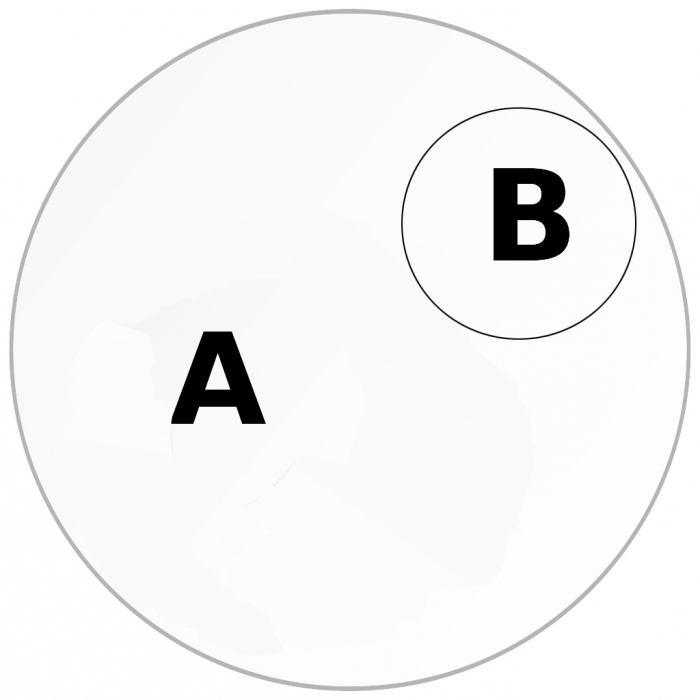
Jēdziens B būs pakārtots attiecībā uz koncepciju A. Tā kā priedes attiecas uz kokiem, jēdziens A šajā piemērā kļūst par pakārtotu, “absorbējot” jēdziena B apjomu.
Attiecības raksturo divus vai vairākus jēdzienus, kas ir savstarpēji izslēdzoši, bet kas pieder pie kāda kopēja vispārēja apļa. Piemēram:
A - klarnete;
B - ģitāra;
C - vijole;
D ir mūzikas instruments.
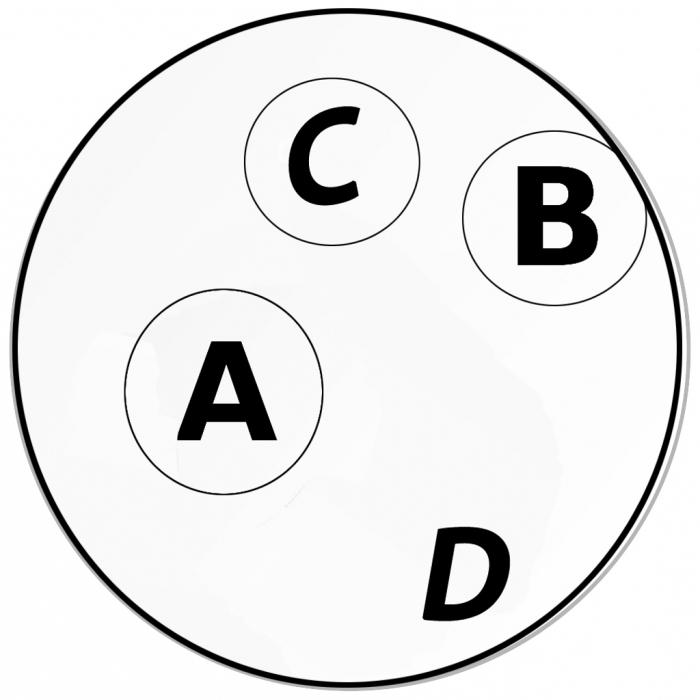
A, B, C jēdzieni nav savstarpēji krustojušies, tomēr tie visi ietilpst mūzikas instrumentu kategorijā (D koncepcija).
Pretēji attiecībām starp koncepcijāmnozīmē, ka šie jēdzieni ir saistīti ar to pašu ģinti. Šādā gadījumā vienam no jēdzieniem ir noteiktas īpašības (iezīmes), bet otrs to noliedz, aizstājot tos ar pretējiem rakstzīmēm. Tādējādi mēs nodarbojamies ar antonīmiem. Piemēram:
A - punduris;
B ir milzis.

Ar pretējām attiecībām starp jēdzieniem Eulera aplis ir sadalīts trīs segmentos, no kuriem pirmais atbilst jēdzienam A, otrais - jēdzienam B, bet trešais - visiem citiem iespējamiem jēdzieniem.
Šajā gadījumā abi jēdzieni pārstāvvienas ģints sugas. Tāpat kā iepriekšējā piemērā, viens no jēdzieniem norāda noteiktas īpašības (atribūtus), bet otrs tos noliedz. Tomēr atšķirībā no pretējās attiecības otrais, pretējais jēdziens neaizstāj noliegtās īpašības ar citām, alternatīvām. Piemēram:
A ir grūts uzdevums;
B ir viegls uzdevums (ne-A).

Izsakot šāda veida jēdzienu loku, Eulera aplisir sadalīts divās daļās - trešā, starpposma saite šajā gadījumā nepastāv. Tādējādi jēdzieni ir arī antonīmi. Šajā gadījumā viens no tiem (A) kļūst pozitīvs (apstiprinot jebkuru zīmi), bet otrais (B vai ne-A) - negatīvs (noliedzot atbilstošo zīmi): "balts papīrs" - "nav balts papīrs", "krievu" vēsture "-" ārzemju vēsture "utt.
Tādējādi jēdzienu apjomu attiecība attiecībā pret otru ir galvenā iezīme, kas nosaka Eulera apļus.
Jums vajadzētu arī nošķirt jēdzienus elementi unkopas, kuru apjomu attēlo Eulera apļi. Komplekta jēdziens ir aizgūts no matemātikas un tam ir diezgan plaša nozīme. Loģikas un matemātikas piemēri parāda to kā sava veida objektu kolekciju. Paši objekti ir šī komplekta elementi. "Daudz ir daudz, iespējams, ka tas ir viens" (Georgs Kantors, kopu teorijas pamatlicējs).
Komplekti tiek apzīmēti ar lielajiem burtiemburti: A, B, C, D ... utt., komplektu elementi - mazie burti: a, b, c, d ... un citi. Komplekta piemēri var būt skolēni vienā klasē, grāmatas noteiktā plauktā (vai, piemēram, visas grāmatas noteiktā bibliotēkā), lappuses dienasgrāmatā, ogas meža klajumā utt.
Savukārt, ja noteikta kopa navnesatur elementus, tad to sauc par tukšu un apzīmē ar Ø. Piemēram, paralēlo līniju krustošanās punktu kopa, vienādojuma x risinājumu kopa2 = -5.
Lai atrisinātu lielu skaitu uzdevumu, aktīviTiek izmantoti Eulera apļi. Loģikas piemēri skaidri parāda saikni starp loģiskajām operācijām un kopu teoriju. Šajā gadījumā tiek izmantotas jēdzienu patiesības tabulas. Piemēram, aplis, kas apzīmēts ar vārdu A, apzīmē patiesības reģionu. Tādējādi apgabals ārpus apļa pārstāvēs melus. Lai noteiktu loģiskas darbības diagrammas laukumu, jums jānoēno apgabali, kas nosaka apli Euler, kurā tā vērtības elementiem A un B būs patiesas.
Eulera apļu izmantošana ir plaši izplatītapraktisks pielietojums dažādās nozarēs. Piemēram, situācijā ar profesionālu izvēli. Ja priekšmetu uztrauc nākotnes profesijas izvēle, viņš var vadīties pēc šādiem kritērijiem:
W - ko man patīk darīt?
D - ko es daru?
P - kā es varu nopelnīt labu naudu?
Attēlosim to diagrammas veidā: Eulera apļi (piemēri loģikā - krustošanās attiecība):

Rezultāts būs tās profesijas, kas atradīsies visu trīs aprindu krustpunktā.
Eulera-Venna apļi ieņem īpašu vietumatemātika (kopu teorija), aprēķinot kombinācijas un īpašības. Eulera elementu kopas apļi ir ieslēgti taisnstūrī, kas apzīmē universālo kopu (U). Apļu vietā var izmantot arī citas slēgtas formas, taču būtība paliek nemainīga. Skaitļi krustojas viens otram atbilstoši problēmas nosacījumiem (vispārīgākajā gadījumā). Arī šie skaitļi ir attiecīgi jāmarķē. Punkti, kas atrodas dažādos diagrammas segmentos, var darboties kā aplūkojamo kopu elementi. Pamatojoties uz to, ir iespējams ēnot konkrētas zonas, tādējādi apzīmējot jaunizveidotos kopumus.

Ar šiem komplektiem ir iespējams izpildītmatemātikas pamatdarbības: saskaitīšana (elementu kopu summa), atņemšana (starpība), reizināšana (reizinājums). Turklāt, pateicoties Eulera-Venna diagrammām, ir iespējams veikt kopu salīdzināšanas darbības pēc tajās iekļauto elementu skaita, tos neskaitot.


























