Īpašības un metodes kvadrātiskā vienādojuma sakņu atrašanai

Pasaule ir veidota tā, lai pieņemtu lielu skaitu lēmumuuzdevumi tiek reducēti līdz kvadrātiskā vienādojuma sakņu atrašanai. Vienādojumu saknes ir svarīgas, aprakstot dažādus modeļus. Tas bija zināms senās Babilonas mērniekiem. Astronomi un inženieri arī bija spiesti risināt šādas problēmas. Jau 6. gadsimtā pirms mūsu ēras indiešu zinātnieks Ariabhata izstrādāja pamatus kvadrātiskā vienādojuma sakņu atrašanai. Gatavo izskatu formulas ieguva 19. gadsimtā.

Vispārīgi jēdzieni

Mēs iesakām iepazīties ar kvadrātvienādojumu pamatlikumiem. Parasti vienlīdzību var uzrakstīt šādi:

ah² + bx + c = 0,

Kvadrātiskā vienādojuma sakņu skaits var būt vienāds ar vienu vai diviem. Ātru analīzi var veikt, izmantojot diskriminējošo personu jēdzienu:

D = b² - 4ac

Atkarībā no aprēķinātās vērtības mēs iegūstam:

• D> 0 ir divas dažādas saknes. Vispārējā formula kvadrātiskā vienādojuma sakņu noteikšanai izskatās (-b ± √D) / (2a).
• D = 0, šajā gadījumā sakne ir viena un atbilst vērtībai x = -b / (2a)
• D <0, ja diskriminējoša viela ir negatīva, vienādojumam nav risinājuma.

Piezīme: ja diskriminējošais ir negatīvs, vienādojumam nav saknes tikai reālo skaitļu reģionā. Ja algebra tiek paplašināta līdz sarežģītu sakņu jēdzienam, tad vienādojumam ir risinājums.

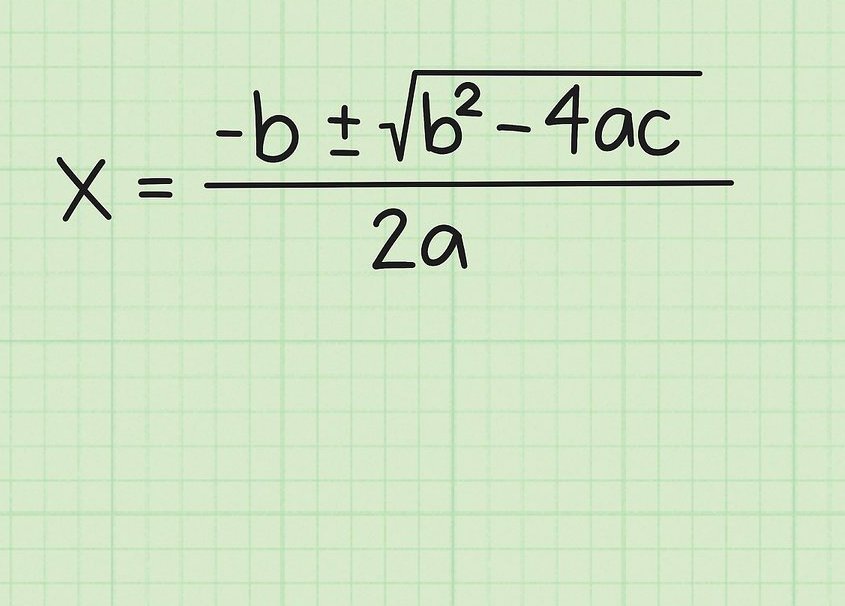
Mēs sniedzam darbību ķēdi, kas apstiprina sakņu atrašanas formulu.

No vienādojuma vispārīgās formas izriet:

ah² + bx = -c

Mēs reizinām labo un kreiso pusi ar 4a un pievienojam b², mēs saņemam

4.a²ar² + 4abx + b² = -4ac + b²

Pārveidojiet kreiso pusi kā kvadrātveida polinomu (2ax + b)²... Veikt vienādojuma 2ax + b = -b ± √ (-4ac + b²), mēs pārnesam koeficientu b uz labo pusi, mēs iegūstam:

2ax = -b ± √ (-4ac + b²)

Tas nozīmē:

x = (-b ± √ (b² - 4ac))

Kas bija jāparāda.

Īpašs gadījums

Dažos gadījumos problēmas risinājumu var vienkāršot. Tātad, lai iegūtu vienmērīgu koeficientu b, mēs iegūstam vienkāršāku formulu.

Mēs apzīmējam k = 1 / 2b, tad kvadrātvienādojuma sakņu vispārējās formas formula ir šāda:

x = (-k ± √ (k² - ac)) / a

Ja D = 0, mēs iegūstam x = -k / a

Vēl viens īpašs gadījums būs vienādojuma a = 1 atrisinājums.

Skatam x² + bx + c = 0 saknes būs x = -k ± √ (k² - c) kad diskriminants ir lielāks par 0. Gadījumam, kad D = 0, sakni noteiks ar vienkāršu formulu: x = -k.

Diagrammu izmantošana

Jebkura persona, pat nezinot, pastāvīgi saskaras ar fiziskām, ķīmiskām, bioloģiskām un pat sociālām parādībām, kuras labi raksturo kvadrātiskā funkcija.

Piezīme: Līkni, kuras pamatā ir kvadrātiskā funkcija, sauc par parabolu.

Šeit ir daži piemēri.

1. Aprēķinot lādiņa trajektoriju, tiek izmantota kustības īpašība gar ķermeņa parabolu, kas izšauta leņķī pret horizontu.
2. Parabola īpašība vienmērīgi sadalīt slodzi tiek plaši izmantota arhitektūrā.

Izprotot paraboliskās funkcijas nozīmi, izdomāsim, kā izmantot grafiku, lai izpētītu tā īpašības, izmantojot jēdzienus "diskriminējošs" un "kvadrātvienādojuma saknes".

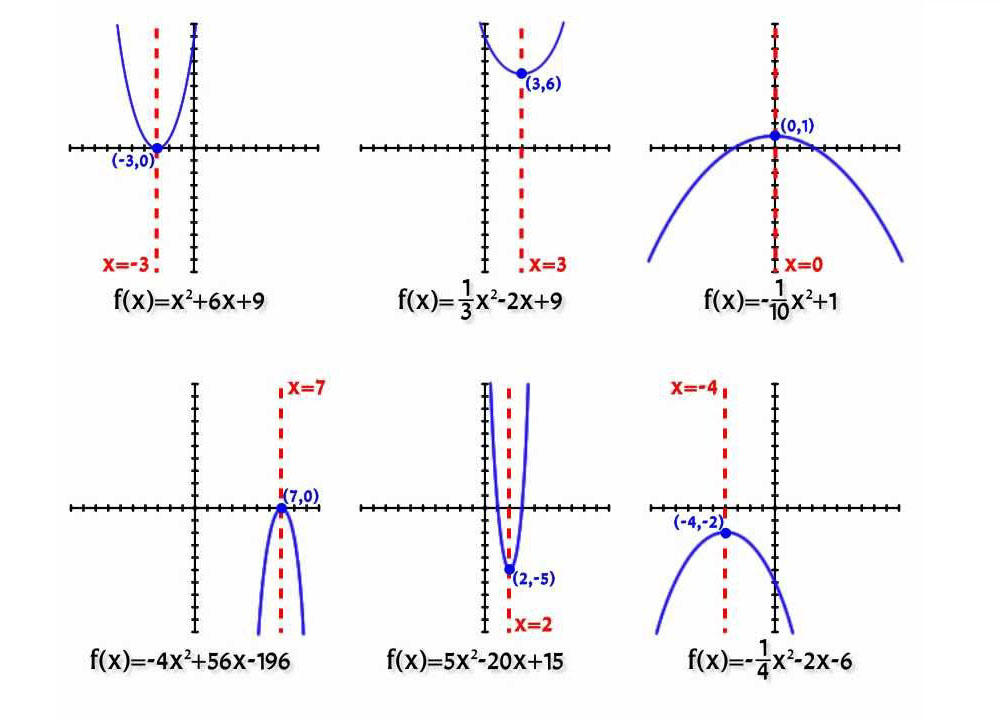
Atkarībā no koeficientu a un b vērtības līknes pozīcijai ir tikai sešas iespējas:

1. Diskriminants ir pozitīvs, a un b ir atšķirīgas zīmes. Parabolas zari ir vērsti uz augšu, kvadrātvienādojumam ir divi risinājumi.
2. Diskriminants un koeficients b ir vienāds ar nulli, koeficients a ir lielāks par nulli. Grafiks atrodas pozitīvajā zonā, vienādojumam ir 1 sakne.
3. Diskriminants un visi koeficienti ir pozitīvi. Kvadrātvienādojumam nav risinājuma.
4. Diskriminants un koeficients a ir negatīvi, b ir lielāks par nulli. Grafa zari ir vērsti uz leju, vienādojumam ir divas saknes.
5. Diskriminants un koeficients b ir vienāds ar nulli, koeficients a ir negatīvs. Parabola skatās uz leju, vienādojumam ir viena sakne.
6. Diskriminants un visi koeficienti ir negatīvi. Risinājumu nav, funkciju vērtības pilnībā atrodas negatīvajā zonā.

Piezīme: opcija a = 0 netiek ņemta vērā, jo šajā gadījumā parabola deģenerējas taisnā līnijā.

Visu iepriekš minēto labi ilustrē zemāk redzamais attēls.

Problēmu risināšanas piemēri

Nosacījums: izmantojot vispārīgās īpašības, izveidojiet kvadrātvienādojumu, kura saknes ir vienādas ar otru.

Risinājums:

pēc problēmas x stāvokļa₁ = x₂, vai -b + √ (b² - 4ac) / (2a) = -b + √ (b² - 4ac) / (2a). Ieraksta vienkāršošana:

-b + √ (b² - 4ac) / (2a) - (-b - √ (b² - 4ac) / (2a)) = 0, atveriet iekavas un norādiet līdzīgus vārdus. Vienādojums ir 2√ (b² - 4ac) = 0. Šis apgalvojums ir patiess, ja b² - 4ac = 0, tātad b² = 4ac, tad vienādojumā tiek aizstāta vērtība b = 2√ (ac)

ah² + 2√ (ac) x + c = 0, reducētā formā iegūstam x² + 2√ (c / a) x + c = 0.

Atbilde:

ja a nav vienāds ar 0 un jebkurš c, ir tikai viens risinājums, ja b = 2√ (c / a).

Kvadrātvienādojumi ar visu to vienkāršībuir liela nozīme inženiertehniskajos aprēķinos. Gandrīz jebkuru fizisku procesu var aprakstīt ar zināmu tuvinājumu, izmantojot n pasūtījuma jaudas funkcijas. Pirmais šāds tuvinājums būs kvadrātvienādojums.