
Skaitīšanas nepieciešamība kļuva acīmredzamacilvēks no primitīvas sabiedrības veidošanās sākuma. Viņu skaitliskās sistēmas ar īpašiem ciparu apzīmējumiem tika izveidotas visos izolētajos civilizācijas centros: Ēģiptē un Senajā Babilonā, Ķīnā un Indijā, Dienvidamerikas indiāņu vidū un senajā Grieķijā. Matemātika ir pārgājusi no vienkāršas pamatskaitīšanas uz sarežģītu topoloģijas teoriju risināšanu. Turklāt nulles skaitļa vēsture satur tikai nelielu daļu no šī perioda.

No latīņu valodas nullis ("nē") nāca vārds,apzīmē vienu no svarīgākajiem matemātiskajiem jēdzieniem. Tajā ir ne tikai simbols - skaitlis, kas palīdz sekot līdzi, reģistrēt matemātiskās operācijas. Tas ir viss jēdziens. Jebkāda daudzuma, tukšuma, sākuma un bezgalības neesamība - filozofiskā attieksme pret šiem jēdzieniem bija atšķirīga dažādos laikmetos, dažādās pasaules izpratnes sistēmās.
Aizvēsturiskos laikos svina kalkulupalīdzēja pirksti un kāju pirksti. Ciparu dalījums piecās un desmitās, ar to ir saistīta decimālo skaitļu sistēmas izcelsme. Lai atvieglotu šīs operācijas, tika izmantoti griezumi uz koka un dzīvnieku kauliem, serifi uz akmeņiem un oļi. čaumalas un citi mazi priekšmeti. Katrs šāds elements apzīmē noteiktu numuru. Praktiskākajiem skaitliskajiem modeļiem ir līdzīgs raksturs. Šādas sistēmas sauc par pozicionālām - ciparu vērtību, rakstot ciparus, nosaka to atrašanās vieta vai izlāde.
Pretējas pieejas piemērs un pielietojumsLīdz šim šī sistēma ir skaitļu rakstīšanas veids, kas datēts ar seno Romu. Tajā vienību apzīmēšanai izmantoti desmiti, simti latīņu alfabēta burtu.

Счётная доска, состоящая из углублений, kas atbilst noteiktām kategorijām, kurās ietilpst oļi vai krelles, tas ir pazīstams dažādu tautu un laikmetu kultūrām. Ir zināmas arī citas abaka šķirnes - virves ar mezgliem vai auklas ar pērlītēm. Nākamais solis šādas ierīces attīstībā bija rādītāji, kas tika izmantoti pirms kalkulatoru parādīšanās.
Skaitļa nulles vēsture ir notikumu processmatemātiskā koncepcija un to apzīmējošā simbola lietošanas sākums. Gan abacus, gan partitūras savā ziņā ir skaitļu sērijas vizualizācijas līdzeklis. Tukša vieta attiecīgajā padziļinājumā vai neesoša kontu darbība ļāva abstraktajam nulles jēdzienam kļūt skaidram. Simbols, kas to apzīmē, vispirms parādījās senās Babilonas matemātiķu un astronomu vidū.

Civilizācijā, kas dzimusi starp Tigris unTika pieņemta skaitliskā sistēma, kas mantota no seniem šumeriem. Tas bija pozicionāls - skaitļu nozīme bija atkarīga no pozīcijas attiecībā pret citiem skaitļiem. Izstrādāts 4-5 tūkstošus gadu pirms mūsu ēras. piemēram, tas tika uzbūvēts uz numuru 60. Tāpēc seno Babilonijas inženieru un astronomu izmantotie matemātiskie aprēķini izskatījās diezgan apgrūtinoši un neērti. Lai veiksmīgi darbotos ar cipariem, jums no sirds bija jāatceras vai acu priekšā vajadzētu būt skaitļu reizināšanas rezultātiem no 1 līdz 60.
Skaitlis nulle vai zīme, kuru babilonieši pieņēmaizlādes apzīmējumi izskatījās kā divi ķīļi vai bultas, kas novietotas leņķī. Šis simbols bija skaitļa neatņemama sastāvdaļa un nepiedalījās aritmētiskajās operācijās - to nebija iespējams pievienot vai reizināt.

Neatkarīgi no Mezopotāmijas matemātiķiem Centrālamerikas indiāņi - maiji un inki - ieviesa savu nulli ikdienas dzīvē. Abām skaitļu sistēmām kopīgi bija tas, ka viņi neizstrādāja ideju par nulli kā skaitli.
Senās Amerikas civilizācija pameta pasaulidaudzi sasniegumi intelektuālajā jomā. Maiju un inku sarežģītās kalendāra sistēmas ir gadsimtu pieredzes rezultāts astronomiskos novērojumos un sarežģītos matemātiskos aprēķinos. Bet nekad viņu vienādojumos cipars nulle nebija skaitlis, kas ietekmē matemātisko darbību rezultātu.

Seno grieķu matemātiķu galvenais mantojumsbija viņu sasniegumi ģeometrijā un astronomijā. Skaitļi to attēlojumā ir segmenti, kuriem ir sākums, beigas un noteikts garums. Nulle ir skaitlis, kuram šajā gadījumā nav praktiskas vērtības. Segmentam ar nulles garumu senajā matemātikā un filozofijā nebija jēgas.
Viens no galvenajiem Aristoteļa mācību principiemir frāze Natura abhorret vakuums - "Daba atstāj vakuumu". Bezgalība, nekas, neesamība - šīs kategorijas neiederējās senajā Visumā. Tāpēc jautājuma "kāds skaitlis ir 0" mūsdienu nozīme nebija sasniedzama Arhimēdam, Pitagoram vai Eiklidam, kaut arī simbols, kas līdzīgs nullei, ir atrodams lielā astronoma Ptolemaja tabulās. Burtu "Omicron" (pirmais burts vārdā οὐδέν - "nekas") viņš nolika tukšās šūnās.
Ko izgudroja Indijas matemātiķi?Mahavira (850), Brahmagupta (1114), Ariabhata (476) ir traktātu autori, kuros lielā mērā ir izveidojusies mūsdienu skaitļu reģistrēšanas sistēma un aritmētisko pamatdarbību likumi. Vēsturnieki uzskata, ka decimālo skaitļu sistēmu indieši aizņēmās no ķīniešiem, bet tās pozicionālo raksturu - no babiloniešiem. Tiek uzskatīts, ka nulles simbolu indieši aizņēmās arī no Ptolemaja darbiem.
Pirmais formulētais matemātiķispilnīga skaitļu sistēma, kas līdz šai dienai paliek nemainīga un kalpo lielākajai daļai cilvēces, bija Bagdādē dzīvojošais Horezmi Muhameds bin Musa (787-850). Viņa Indijas kontu grāmatā ir detalizēti aprakstīti deviņi arābu cipari un atbildēts uz jautājumu "Vai 0 ir skaitlis?" Nulle šajā grāmatā tiek uzskatīta par pirmo. Šī darba tulkojums latīņu valodā kļuva plaši pazīstams Eiropā XII gadsimtā un lika pamatu Austrumu matemātikas zināšanu izplatībai.
Atšķirībā no eiropiešiem, austrumniekiem ir mūžībafilozofi bija bijību iedvesmojoši. Tāpēc nulle seno Indijas zinātnieku vienādojumos beidzot kļuva ne tikai par simbolu vienību neesamībai attiecīgajā kategorijā, bet arī par dabisko skaitli, kas ietekmē aprēķinu rezultātu. Pievienojot nulli, reizinot ar 0 - tas viss ir ieguvis jēgpilnu matemātisko darbību nozīmi.

Arī pats skaitļu no 1 līdz 0 rakstīšana ieguva savu galīgo formu, pateicoties senajiem Indijas matemātiskajiem traktātiem un tiem simboliem, kurus Eiropā parasti sauc par arābu, paši arābi sauc par indiāņiem.
Skaitļa "nulle" vēsture ir atspoguļota etimoloģijāmatemātikas pamattermi. Vārdam "cipars" ir saknes arābu valodā, un tas nāk no vārda "al-sifr", kas nozīmē "tukšs, nulle". Angļu valoda "nulle" neskaidri atgādina "zefīru" - vēju no austrumiem - tieši no austrumiem galīgā, racionālā un ērtā numuru sistēma nonāca Eiropā.
Viens no galvenajiem Eiropas propagandistiemSlavenais itāļu matemātiķis Leonardo Fibonači kļuva par arābu digitālo sistēmu. Viņa darbs "Abaka grāmata" (1202) iepazīstināja Eiropas zinātniekus ar simboliem un noteikumiem, pēc kuriem arābi raksta matemātiskas darbības. Pirmie, kas novērtēja austrumu matemātiskā modeļa ērtības un racionalitāti, bija tie, kas pieraduši pie ikdienas apstrādes ar numuriem - baņķieri un tirgotāji. Viņi ātri pieņēma arābu tirgotāju ciparu sistēmu un numuru rakstīšanu. Bet šīs zināšanas Eiropas zinātniskajā praksē ienāca tikai pēc 4 gadsimtiem, aizstājot seno sistēmu, kuru pieņēma Eiropas matemātiķi.
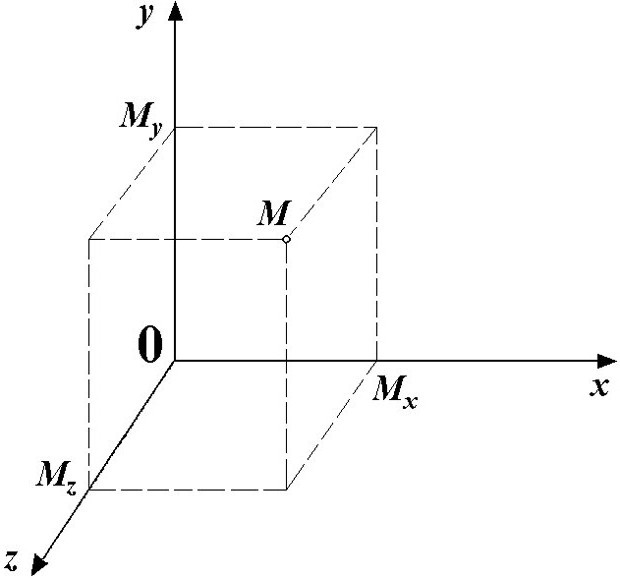
Nulle ieguva nozīmi ar ievadu zinātniskajātaisnstūra koordinātu sistēmas izmantošana, ko 17. gadsimtā ierosināja Renē Dekarts. Nulle, kas atrodas centrā, ir ieguvusi redzamu un vizuāli saprotamu trīs koordinātu asu atskaites punkta nozīmi.
Krievijā nulle tika ieviesta praksē ar slavenā mācību grāmatas "Aritmētika, tas ir, skaitļu zinātne" (1703) autora Leontija Magņitska centieniem.
Nulle, kas atšķir pozitīvo unnegatīvie skaitļi, tam ir unikālas matemātiskās īpašības. Tas ir vienmērīgs, neparakstīts dabiskais vesels skaitlis. Saskaitot ar nulli un atņemot nulli, skaitlis nekādā veidā neietekmē, un, reizinot ar 0, iegūst nulli. Dalīšana ar nulli tiek uzskatīta par bezjēdzīgu darbību, kas, ja to izpilda datorprogrammā, var nodarīt būtisku kaitējumu sistēmai.
Neveiksmes nozīme izrādījās mēģinājumā dalīt ar 0ASV Jūras spēku kreisera Yorktown datorsistēmā, kas notika 1997. gada rudenī un noveda pie neatļautas piedziņas sistēmas izslēgšanas. Nepareiza attieksme pret skaitli, kas nozīmē "nekas", spēcīgu kara kuģi pārvērta par bezpalīdzīgu stacionāru mērķi.
Šī skaitļa vērtība ievērojami palielinājās nozinātnes attīstība. Nulle rodas ne tikai matemātiskās jomās. Dzirdamības slieksnis akustikā tiek pieņemts kā 0. Kāds skaitlis ir daudzu mērinstrumentu skalas sākumā, students arī zina: 0 pēc Celsija skalas ir ūdens sasalšanas punkts, garuma izcelsme ir galvenais meridiāns. utt.
Binārais apzīmējums, kas kalpoja par pamatumūsdienu skaitļošanas ierīču izveide ir pozicionālo skaitļu sistēma ar otro pamatu. Tas nozīmē, ka visi datorsistēmās ievadītie dati tiek kodēti, apvienojot divas rakstzīmes - vienu un nulli.

Datoru loma mūsdienu pasaulē kļūst izšķiroša attiecībā uz visiem dzīves aspektiem, kas nozīmē, ka turpinās skaitļa nulle vēsture, bez kuras to izskats nebūtu bijis iespējams.


























