
Matemātiskās noslēpumi ir neiedomājamisumma. Katrs no tiem ir unikāls savā veidā, bet to šarmu slēpjas faktā, ka risinājumam neizbēgami ir jāpiedalās formulās. Protams, jūs varat mēģināt tos atrisināt, kā saka, poking, bet tas būs ļoti garš un gandrīz neveiksmīgs.
Šis raksts runās par vienu nošādas mistērijas, un precīzāk - par burvju laukumu. Mēs detalizēti analizēsim, kā atrisināt burvju laukumu. Protams, vispārējās izglītības programmas 3. pakāpe iet, bet varbūt ne visi saprata vai vispār neatceras.
Burvju laukums, vai, kā to sauc,maģija, ir tabula, kurā kolonnu un rindu skaits ir vienāds, un tie visi ir piepildīti ar atšķirīgiem numuriem. Galvenais uzdevums ir nodrošināt, lai šie skaitļi vertikālā, horizontālā un diagonālā daudzumā piešķirtu vienādu vērtību.
Помимо магического квадрата, есть еще и daļēji burvju. Tas nozīmē, ka skaitļu summa ir vienāda vertikāli un horizontāli. Burvju laukums ir "normāls" tikai tad, ja uzpildīšanai tiek izmantoti dabiskie skaitļi no viena.
Ir arī tāda lieta kā simetrisks burvju laukums - tas ir tad, kad divu ciparu summas vērtība ir vienāda, kad tie ir izvietoti simetriski attiecībā pret centru.
Ir arī svarīgi zināt, ka kvadrāti var būt jebkura izmēra, kā arī 2 līdz 2. Kvadrāts no 1 līdz 1 tiek uzskatīts arī par maģiju, jo visi nosacījumi ir izpildīti, lai gan tas sastāv no viena numura.
Tātad, mēs esam izlasījuši definīciju, tagad parunāsim par to, kā atrisināt burvju laukumu. Skolas mācību programmas 3. klase, visticamāk, izskaidrotu visu, kas ir tik detalizēti kā šis raksts.
Tie cilvēki, kuri zina, kā atrisināt burvjukvadrāts (3. klase noteikti zina), viņi nekavējoties saka, ka ir tikai trīs risinājumi, un katrs no tiem ir piemērots dažādiem laukumiem, tomēr nav iespējams ignorēt ceturto risinājumu, proti, “nejauši”. Patiešām, zināmā mērā ir iespējams, ka nezinādams cilvēks joprojām spēs atrisināt šo mīklu. Taču mēs šo metodi izmetīsim garā lodziņā un turpināsim tieši pie formulām un metodēm.
Šī metode ir piemērota tikai šāda laukuma risināšanai, kurā šūnu skaits ir nepāra, piemēram, 3 ar 3 vai 5 ar 5.
Tātad, jebkurā gadījumā, vispirms ir jāatrod burvju konstante. Tas ir numurs, kas tiks iegūts, skaitot pa diagonāli, vertikāli un horizontāli. To aprēķina, izmantojot šādu formulu:
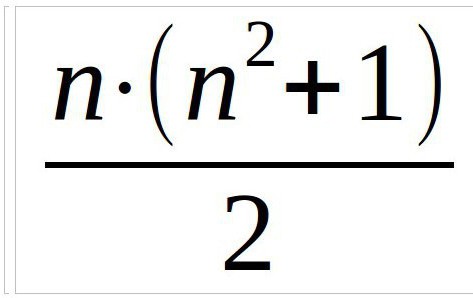
Šajā piemērā mēs izskatīsim trīs trīs kvadrātu, tāpēc formula izskatīsies šādi (n ir kolonnu skaits):
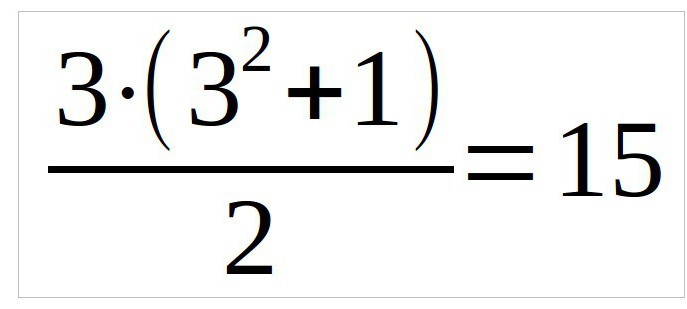
Tātad, mums ir kvadrāts. Pirmais, kas jādara, ir ievadīt numuru pirmās rindas centrā augšpusē. Visiem turpmākiem numuriem jābūt novietotiem pa labi uz diagonālā.
Bet tad rodas jautājums, kā atrisināt maģijukvadrātveida? Maz ticams, ka 3. kategorija izmantos šo metodi, un vairākumam būs problēma, kā to darīt šādā veidā, ja šādas šūnas nav? Lai to izdarītu pareizi, jums ir nepieciešams ieslēgt iztēli un uzvilkt līdzīgu burvju laukumu uz augšu, un izrādās, ka numurs 2 būs tajā apakšējā labajā šūnā. Tātad, mūsu laukumā mēs ievadām divus vienā vietā. Tas nozīmē, ka mums ir jāievada skaitļi tā, lai kopā tie sniegtu vērtību 15.
Turpmākie numuri atbilst tieši tādiem pašiem.Tas nozīmē, ka 3 būs pirmās slejas centrā. Bet 4 par šo principu nevarēs ieiet, jo tās vietā jau ir vienība. Šajā gadījumā numurs 4 tiek ievietots zem 3 un turpinās. Pieci - kvadrāta centrā, 6 - augšējā labajā stūrī, 7 - zem 6, 8 - augšējā kreisajā un 9 - apakšējās līnijas centrā.
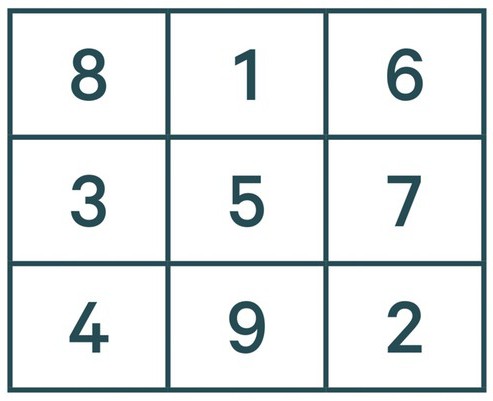
Tagad jūs zināt, kā atrisināt burvju laukumu.3.skaitlis Demidovs pagājis, bet šim autoram bija nedaudz vienkāršāks uzdevums, tomēr, zinot šo metodi, būs iespējams atrisināt jebkuru šādu problēmu. Bet, ja kolonnu skaits ir nepāra. Un ko darīt, ja, piemēram, ir 4 kvadrātmetri? Par to tālāk tekstā.
Dubultās paritātes kvadrāts ir tas, kurā kolonnu skaitu var iedalīt 2 un 4. Tagad mēs uzskatām kvadrātu 4 ar 4.
Tātad, kā atrisināt burvju laukumu (3. klase, Demidovs, Kozlovs, Tonkikh - uzdevums matemātikas mācību grāmatā), kad tā kolonnu skaits ir 4? Ļoti vienkāršs. Vieglāk nekā iepriekš.
Vispirms mēs atrodam burvju konstantu līdztā pati formula, kas tika citēta pēdējo reizi. Šajā piemērā skaitlis ir 34. Tagad jums ir jāizveido skaitļi tā, lai vertikālā, horizontālā un diagonālā summa būtu vienāda.
Vispirms jums ir jāglezno dažas šūnas,to var izdarīt ar zīmuli vai iztēli. Mēs gleznojam pār visiem stūriem, ti, augšējo kreiso un augšējo labo pusi, apakšējo kreiso un apakšējo labo pusi. Ja laukums bija 8 līdz 8, tad ir nepieciešams krāsot ne vienu šūnu stūrī, bet četrus, 2 - 2 izmērus.
Tagad ir nepieciešams gleznot virs šī laukuma centra, lai tā stūri pieskartos jau nokrāsoto šūnu stūriem. Šajā piemērā mēs iegūstam kvadrātu 2 līdz 2.
Darba sākšana.Mēs aizpildīsim no kreisās uz labo pusi tādā secībā, kādā atrodas šūnas, tikai mēs ievadīsim vērtību aizpildītajās šūnās. Izrādās, ka augšējā kreisajā stūrī mēs ievadām 1, pa labi - 4. Tad aizpildām centrālo 6, 7 un vēl 10, 11. Apakšējā kreisajā pusē 13 un pa labi - 16. Mēs domājam, ka aizpildīšanas secība ir skaidra.

Atlikušās šūnas tiek aizpildītas tieši tādā pašā veidā, tikaidilstošā secībā. Tas ir, tā kā pēdējais ierakstītais skaitlis bija 16, kvadrāta augšdaļā rakstām 15, tad 14. Tad 12, 9 un tā tālāk, kā parādīts attēlā.
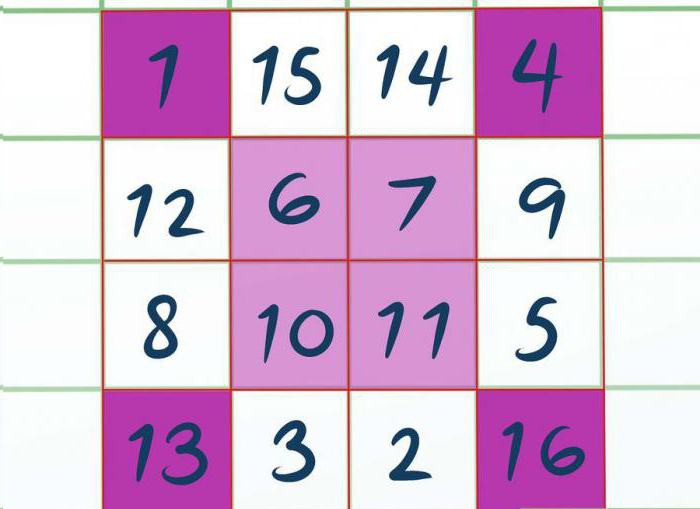
Tagad jūs zināt otro veidu, kā atrisināt burvju laukumu. 3. pakāpe piekrīt, ka dubultparitātes laukumi ir daudz vieglāk atrisināmi nekā citi. Nu, mēs ejam uz pēdējo metodi.
Viena paritātes kvadrātu sauc, šis laukums, kura kolonnu skaitu var iedalīt divās, bet ne četrās. Šajā gadījumā tas ir 6 x 6 kvadrātmetri.
Tātad, mēs aprēķinām burvju konstantu. Viņa ir vienāda 111.
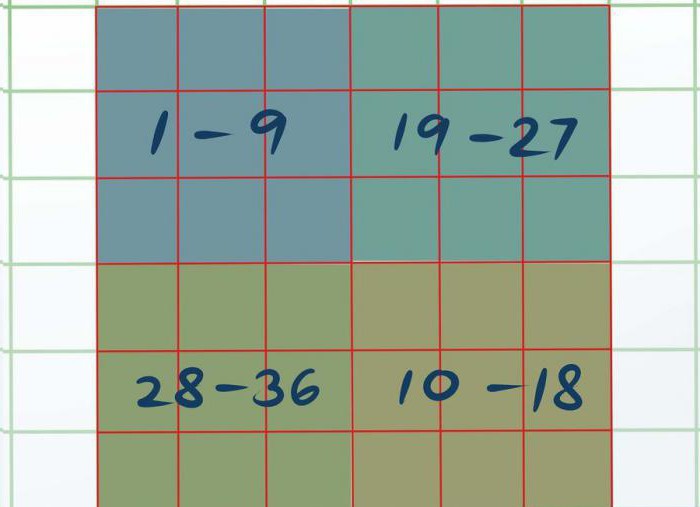
Tagad mums ir nepieciešams vizuāli sadalīt mūsu laukumučetri dažādi kvadrāti no 3 līdz 3. Būs četri mazi kvadrāti, kuru izmēri ir 3 ar 3 vienā lielā 6 līdz 6. Augšējā kreisā daļa tiek saukta A, apakšējā labajā pusē ir B, augšējā labajā pusē ir C un apakšējā kreisajā ir D.

Tagad ir nepieciešams katrs nelielais laukumsatrisināt, izmantojot pirmo metodi, kas dota šajā rakstā. Izrādās, ka laukumā A būs skaitļi no 1 līdz 9, B - no 10 līdz 18, C - no 19 līdz 27 un D - no 28 līdz 36.
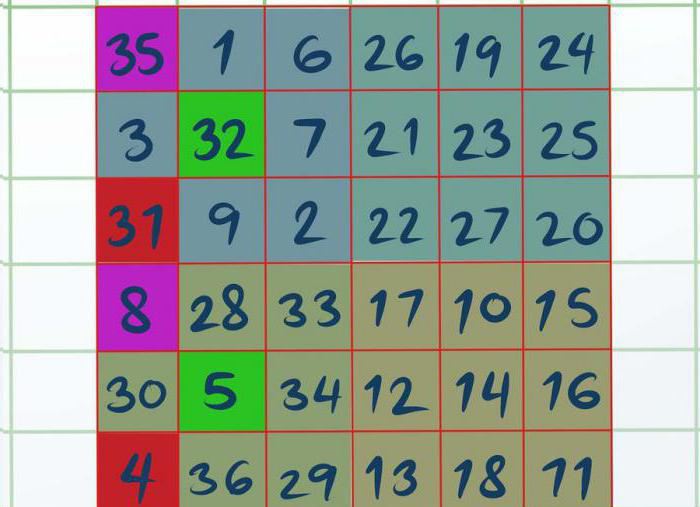
Как только вы решили все четыре квадрата, работа sāksies virs A un D. Vizuāli vai ar zīmuli ir jāizvēlas trīs šūnas A laukumā: augšējā kreisajā, centrālajā un apakšējā kreisajā pusē. Izrādās, ka izceltie numuri ir 8, 5 un 4. Tādā pašā veidā jāizceļ kvadrāts D (35, 33, 31). Viss, kas paliek, ir apmainīt piešķirtos ciparus no kvadrāta D uz A.
Tagad jūs zināt pēdējo veidu, kā atrisināt burvju laukumu. 3 klases kvadrātveida viena paritāte nepatīk visvairāk. Un tas nav pārsteidzoši, ka no visiem tiem, kas ir iesnieguši, tas ir vissarežģītākais.
Прочтя данную статью, вы узнали, как решить burvju laukums. 3. klase (Moro - mācību grāmatas autors) piedāvā līdzīgus uzdevumus tikai ar dažām aizpildītām šūnām. Nav jēgas izskatīt viņa piemērus, jo, zinot visas trīs metodes, jūs varat viegli atrisināt visas ierosinātās problēmas.


























