
Informatica als wetenschap van verzameltechnieken,Het ordenen en verwerken van verschillende gegevens begint zijn ontwikkeling in het midden van de twintigste eeuw. Hoewel sommige historici geloven dat het begin van de vorming van informatica in de 17e eeuw lag, met de uitvinding van de eerste mechanische rekenmachine, associëren de meesten het met het tijdperk van meer geavanceerde computertechnologie. In de jaren 40 van de 20e eeuw, met de komst van de eerste computers, kreeg de informatica een nieuwe impuls in de ontwikkeling.
Het was met de komst van de eerste computerser was behoefte aan de ontwikkeling van nieuwe methoden voor systematisering, berekening en verwerking van grote hoeveelheden gegevens, en aan de ontwikkeling van algoritmen waarmee het volledige potentieel van nieuwe computers zou kunnen worden benut. De informatica kreeg de status van een onafhankelijke wetenschappelijke discipline en ging van het vlak van wiskundige berekeningen naar de studie van berekeningen in het algemeen.

Alle moderne informatica is gebaseerd oplogische bewerkingen. Ze kunnen een fundamenteel onderdeel worden genoemd. Bij het programmeren van computersystemen is het concept van een logische operatie een soort actie, na de uitvoering waarvan een nieuw concept of betekenis wordt gegenereerd, die wordt gevormd op basis van reeds bestaande concepten. De set van dergelijke acties kan variëren, afhankelijk van het processorelement dat de opdrachten moet uitvoeren. Er zijn echter enkele bewerkingen die voor bijna alle bestaande systemen gelden. Dit zijn bewerkingen die werken met de inhoud van de waarden zelf, bijvoorbeeld negatie, of die de kwantitatieve kenmerken van een concept veranderen - optellen, aftrekken, vermenigvuldigen, delen.
Omdat de algebra van logica inhoudt dat er wordt gewerkt aanabstracte concepten, dan werken gegeneraliseerde gegevenstypen als operanden van alle logische bewerkingen. De klassieke elementen waarmee propositionele algebra werkt, zijn proposities, onwaar of waar. In elektronica en programmeren worden booleans true en false, of de integerwaarden 1 (true) en 0 (false), gebruikt om deze termen te beschrijven. De combinatie van deze waarden, hoe ongelooflijk het ook mag klinken, is verbonden met het werk van de meest complexe en grootschalige systemen. Alle programmacode die op een computer of een ander digitaal apparaat wordt uitgevoerd, wordt dynamisch vertaald in een reeks enen en nullen - een universele code die door elke processor kan worden verwerkt.
Zoals eerder vermeld, in de klassiekerBooleaanse algebra, er zijn 2 soorten functies. Logische basisbewerkingen op binaire gegevenstypen zijn acties die de instructie zelf beïnvloeden (unaire of unaire bewerking). Dit omvat ook bewerkingen die nieuwe instructies genereren op basis van bestaande waarden (binaire bewerkingen of twee plaatsen). De volgorde van logische bewerkingen is dezelfde als bij het uitvoeren van wiskundige berekeningen: van links naar rechts, inclusief haakjes.

De meest eenvoudige en een van de bekendsteBooleaanse logische functie is de negatiefunctie. Deze eenvoudigste logische bewerking is het tegenovergestelde van de invoeroperand. In de elektronica wordt deze actie ook wel inversie genoemd. Als u bijvoorbeeld het oordeel "waar" omkeert, is het resultaat "onwaar". Omgekeerd zal het negeren van de waarde "false" resulteren in de waarde "true". Zo'n logische bewerking bij het programmeren wordt heel vaak gebruikt om algoritmen te vertakken en de "selectie" van de volgende set instructies te implementeren op basis van de resultaten die al beschikbaar zijn of gewijzigde omstandigheden.
Gebruikt in programmeren en informaticabeperkte reeks binaire (binaire) bewerkingen. Ze krijgen hun naam van het Latijnse woord bi, wat 'twee' betekent, en zijn een soort functie die twee argumenten als invoer accepteert en als resultaat een nieuwe waarde retourneert. Waarheidstabellen worden gebruikt om alle functies van Booleaanse algebra te beschrijven.
Dit systeem is samengesteld voor een specifiekhet aantal invoeroperanden en beschrijft alle resulterende waarden die een bepaalde logische bewerking kan retourneren voor een bepaalde set invoerparameters.
De meest gebruikte functies in de informatica en computers zijn logische optel- (disjunctie) en logische vermenigvuldigings- (conjunctie) bewerkingen.
De logische AND-bewerking is een functie naar keuzede kleinste van twee of n invoeroperanden. Aan de ingang kan deze functie twee (binaire functie), drie waarden (ternair) of een onbeperkt aantal operanden (n-ary-bewerking) hebben. Bij het evalueren van het resultaat van de functie, zal dit de kleinste van de geleverde invoerwaarden zijn.
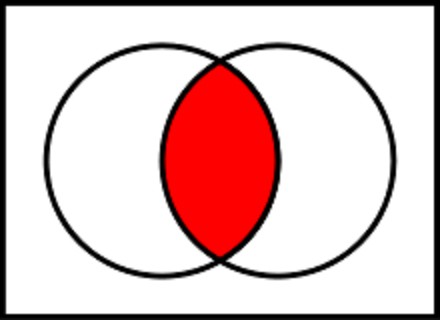
Een analoog in gewone algebra is de functievermenigvuldiging. Daarom wordt de conjunctiebewerking vaak logische vermenigvuldiging genoemd. Bij het schrijven van een functie is het teken het vermenigvuldigingsteken (punt) of het ampersant. Als je een waarheidstabel voor deze functie compileert, zul je zien dat de functie de waarde "true" of 1 aanneemt, alleen als alle invoeroperanden waar zijn. Als ten minste één van de invoerparameters gelijk is aan nul, of de waarde "false", dan is het resultaat van de functie ook "false".

Dit weerspiegelt de analogie met rekenkundige vermenigvuldiging: Het vermenigvuldigen van een willekeurig getal en een reeks getallen met 0 levert altijd 0 op. Deze logische bewerking is commutatief: de volgorde waarin de invoerparameters worden ontvangen, heeft geen invloed op het uiteindelijke resultaat van de berekening.
Een andere eigenschap van deze functie isassociativiteit, of combinatie. Deze eigenschap maakt het mogelijk om de volgorde van berekening te negeren bij het berekenen van een reeks binaire bewerkingen. Daarom is het voor 3 of meer opeenvolgende logische vermenigvuldigingsbewerkingen niet nodig om haakjes te gebruiken. Bij het programmeren wordt deze functie vaak gebruikt om ervoor te zorgen dat specifieke opdrachten alleen worden uitgevoerd als aan bepaalde voorwaarden is voldaan.
Logische bewerking "OF" - een soort Booleaanse functie,wat analoog is aan algebraïsche optelling. Andere namen voor deze functie zijn logische optelling, disjunctie. Net als een logische vermenigvuldigingsbewerking, kan een disjunctie binair zijn (bereken een waarde op basis van twee argumenten), ternair of n-ary.

Waarheidstabel voor een bepaalde logische bewerkingis een soort alternatief voor conjunctie. De logische OR-bewerking berekent het maximale resultaat van de opgegeven argumenten. Disjunctie krijgt de waarde "false", of 0, alleen als alle invoerparameters de waarde 0 ("false") hebben. In elk ander geval zal de uitvoer "waar" zijn, of 1. Om deze functie te schrijven, wordt het wiskundige optelteken ("plus") of twee verticale strepen meestal gebruikt. De tweede optie is gebruikelijk in de meeste programmeertalen en verdient de voorkeur omdat u hiermee een logische bewerking duidelijk kunt onderscheiden van een rekenkundige bewerking.
Logische basisbewerkingen, of ze nu unair zijn,binaire, ternaire of andere functies zijn onderworpen aan bepaalde regels en eigenschappen die hun gedrag beschrijven. Een van die fundamentele eigenschappen die de hierboven beschreven logische functies hebben, is commutativiteit.

Deze eigenschap zorgt ervoor dat de permutatieplaatsen van operanden verandert de waarde van de functie niet. Niet alle operaties hebben deze eigenschap. In tegenstelling tot conjunctie en disjunctie, die voldoen aan de vereisten van commutativiteit, is de matrixvermenigvuldigingsfunctie niet zo, en het veranderen van de factoren in deze bewerking zal het resultaat veranderen, evenals machtsverheffen.
Een andere belangrijke eigenschap die vaak in elektronica en schakelingen wordt gebruikt, is de ondergeschiktheid van paren logische bewerkingen aan de wetten van de Morgan.

Deze wetten verbinden paren van logische bewerkingen metmet behulp van de logische negatiefunctie, dat wil zeggen, ze stellen u in staat de ene logische bewerking uit te drukken met een andere. De functie van negatie van een conjunctie kan bijvoorbeeld worden uitgedrukt met behulp van een disjunctie van negaties van individuele operanden. Met behulp van deze wetten kunnen logische bewerkingen "EN", "OF" onderling worden uitgedrukt en geïmplementeerd met minimale hardwarekosten. Deze eigenschap is buitengewoon handig in schakelingen, omdat het bronnen bespaart bij het berekenen en vormgeven van microschakelingen.


























