Programmeren. Elementaire algoritmische constructies

Om programma's te maken, heb je basis nodigalgoritmische constructies. Hieronder volgt de eenvoudigste manier om problemen op te lossen. Het kan bijvoorbeeld worden gebruikt om met voorbeelden van hetzelfde type te werken. Er zijn ook andere typen: branching en looping. Ze zullen in dit artikel worden besproken. Maar eerst moet u begrijpen wat het algoritme als geheel is.

algoritme

Het woord "algoritme" komt van het Latijnse algoritmi. Wat betekent het? Het authentieke woord komt van de naam van een wiskundige, wiens activiteit viel in de 9e eeuw. Dankzij de verhandeling al-Khwarizmi kon de mensheid kennis maken met het basistype van algoritmische constructie en, in het algemeen, met een algemeen concept.

Eerder werd de vorm van het schrijven van het woord aangenomen - "algoritme". Nu wordt het slechts in enkele gevallen gebruikt.

Algoritme is een proces dat verandering betekentinitiële gegevens, die voorkomen in de vorm van discrete stappen. Iedereen komt dit concept in het leven tegen, wie hij ook is. Algoritmen kunnen de bereiding van thee of voedsel worden genoemd, vermenigvuldigen of optellen, vergelijkingen oplossen, enz. Alle huishoudelijke apparaten, waarvan het werkproces geautomatiseerd is, functioneren als gevolg van duidelijke stappen die in het geheugen van de processor zijn geschreven. Dergelijke algoritmen worden huishoudelijke algoritmen genoemd. Er zijn ook andere soorten. Laten we ze eens bekijken.

Soorten algoritmen

De belangrijkste algoritmische constructies zijn onderverdeeld in verschillende typen, die in deze paragraaf worden besproken. Wat zijn zij?

1. Informatief. Dergelijke algoritmen werken met een grote hoeveelheid gegevens, maar het volume van hun verwerking is klein en ongecompliceerd.
2. Managers. Het werk van dergelijke algoritmen wordt geassocieerd met informatie die wordt geleverd vanuit een bepaalde bron. Na ontvangst worden speciale signalen verzonden om de werking van de apparaten te garanderen.
3. Computergebruik. In tegenstelling tot informatiealgoritmen werken de beschreven algoritmen met kleine hoeveelheden gegevens, maar produceren ze een groot proces.

In wezen is het algoritme tot in het kleinste detail nauwkeurigdetails instructie. Niet al deze gegevens kunnen echter het beschreven concept worden genoemd. Om te begrijpen of een algoritme een instructie is of niet, moet u het op bepaalde eigenschappen controleren.

Algoritme-eigenschappen

Alle elementaire algoritmische constructies moeten acties hebben die eraan "gehoorzamen". Laten we dit probleem in meer detail bekijken.

Als je het werk van de algoritmen en huneigenschappen, u kunt zien dat het niet nodig is om hun componenten te begrijpen, vrij duidelijk overeenkomen met het plan. Het juiste resultaat wordt verkregen, zelfs als u zich eenvoudigweg mechanisch houdt aan de nodige acties. Hieruit kunnen we concluderen dat het door het gebrek aan betekenis in het bewustzijn van acties heel goed mogelijk is om het algoritme te geven aan de implementatie van een computer. Met andere woorden, geautomatiseerde apparaten hebben dit proces nodig.

Welke eigenschappen moeten de algoritmische basisconstructies hebben voor het meest nauwkeurige werk?

1. Begrijpelijkheid. Elke opdracht moet zo duidelijk mogelijk zijn voor het uitvoerbare object. Het lijkt erop dat niets gemakkelijker is dan bijvoorbeeld een punt in het midden tekenen, nee, maar totdat er een commando is geschreven waarmee u een actie kunt uitvoeren, is het niet mogelijk om dit te doen.
2. Effectiviteit. Wat houdt deze eigenschap in? Verplichte ontvangst van het resultaat. Het algoritme kan niet anders dan tot een soort antwoord leiden. Als gevolg van een fout krijgt u mogelijk niet het gewenste resultaat, maar het blijft zo. Bovendien moet het antwoord na een bepaald aantal stappen worden ontvangen.
3. Massa karakter. Elk algoritme moet van toepassing zijn op een bepaalde categorie problemen. Ze kunnen van elkaar verschillen in de oorspronkelijke gegevens.
4. Zekerheid. Elke actie mag slechts één betekenis hebben en mag geen afgeleide decodering toestaan. Idealiter, ongeacht hoe vaak het programma wordt uitgevoerd, moet het resultaat altijd hetzelfde zijn.
5. Discretie. Algoritme - opeenvolgende uitvoering van stappen. Elke stap is een commando, u kunt niet overslaan of nieuwe toevoegen.
6. Juistheid. Elk algoritme dat op elk soort probleem van toepassing is, moet voor iedereen correct zijn. Bij het programmeren ontstaan ​​problemen vaak niet bij het schrijven van stappen, die vaak niet veel tijd kosten, maar bij het uitvoeren ervan voor verschillende soorten vragen. Daarom zal een belangrijke stap het debuggen van het algoritme zijn. Daarbij kunnen elementaire algoritmische constructies helpen, waarvan de herhaling tot betere resultaten zal leiden.

Beschrijving van algoritmen

Als we het hebben over methoden voor het schrijven van algoritmen, moet het volgende worden benadrukt:

• Verbaal. Met andere woorden, in een taal die voor de component handig is om zich uit te drukken.
• In tabelvorm. Logischerwijs wordt het algoritme in tabellen geschreven en wordt het in de regel als hulpelement gebruikt.
• Formule-verbaal. Het is gebaseerd op een verbale manier van uitleggen, maar dergelijke acties worden ook in wiskundige formules of symbolen geschreven.
• Grafisch. Zo'n algoritme is geschreven in een speciale blokdiagramtaal.

Het laatste punt moet worden verduidelijkt. Wat is een blokschema? Het is een lineair of niet-lineair algoritme, waarvan de stappen worden geschreven met behulp van speciale blokken. Ze hebben hun eigen configuratie, doel en functie. Bij een dergelijke beschrijving is het algoritme geschreven in blokschema's, die onderling verbonden zijn door lijnen. Ze moeten bovendien een of andere actie (stap) opnemen.

Algoritmische constructies

Sommigen beweren dat algoritmen geen 3 hebbentype, a 4. Algoritmische basisconstructies: lineair, vertakt, cyclisch. Wat de reden is voor dit waanidee, is niet duidelijk. Voor een eenvoudige oplossing van complexe problemen gebruikt de computer de algoritmen van deze drie vrij grote groepen. Laten we ze eens bekijken.

1. Lineair. Zo'n rekenproces kreeg deze naam vanwege het feit dat alle acties in een lineaire volgorde worden uitgevoerd, waarbij elke stap niet meer dan één keer wordt uitgevoerd. Als we naar het taakdiagram kijken, worden de blokken erin onder elkaar geplaatst, afhankelijk van het serienummer van de uitvoering. Lineaire algoritmen werken op zo'n manier dat de richting en betekenis van acties niet veranderen ten opzichte van de oorspronkelijke gegevens. Deze oplossingsmethode is geschikt voor het berekenen van de som of het verschil, de oppervlakte van een figuur of zijn omtrek, enz. Het belangrijkste type algoritmische constructie is het.
2. Forking. Dit rekenproces impliceert de aanwezigheid van een logische uitdrukking (hierna LP) en een keuze van een voorwaarde (vertakkingen "false" en "true"). In elk geval wordt slechts een van de twee of meer commando's geïmplementeerd. Er zijn geen taken en er kunnen ook geen andere opties zijn. Als het algoritme twee vertakkingen heeft, is het eenvoudig, als het meer dan twee is, is het complex. Bovendien wordt het laatste proces gemakkelijk weergegeven ten koste van het eerste. Het belangrijkste type algoritmische constructie is zowel het eerste item als het tweede. In deze lijst is ook de volgende soort opgenomen.
3. Cyclisch. In een dergelijk algoritme zal er noodzakelijkerwijs een element zijn dat vele malen wordt herhaald, terwijl verschillende initiële gegevens worden gebruikt. Met andere woorden, dit proces wordt een cyclus genoemd.

Opgemerkt moet worden dat alle belangrijke algoritmische constructies (volgen, vertakken, lus) met elkaar zijn verbonden, hoewel ze afzonderlijk kunnen worden gebruikt.

Creatie van cycli en hun typen

Wat is er nodig om een ​​cyclus te maken?

• Cyclusteller. Dit is een variabele die de beginwaarde instelt, en wanneer u de actie herhaalt, zal deze veranderen. Het moet in het algoritme worden opgenomen. De basisconstructies van het algoritmische loop-type zullen niet werken zonder.
• De indicator van de bovenstaande gegevens wijzigen voordat de cyclus zelf opnieuw wordt herhaald.
• Het controleren van de toestand voor de computer om te beslissen of hij de cyclus opnieuw moet "herhalen" of dat het niet meer nodig is.

Lussen kunnen deterministisch zijn eniteratief. De eerste is een herhaling van handelingen met een bekend aantal herhalingen. Een iteratieve lus is een lus die een onbeperkt aantal keren wordt herhaald totdat een voorwaarde waar of onwaar wordt.

Basis algoritme

Het is de moeite waard eraan te denken dat de belangrijkstehet basisalgoritme is niet van toepassing op algoritmische constructies. Hoe is hij? Dit concept is lange tijd niet meer in de moderne literatuur gevonden, maar dit betekent niet dat het helemaal niet meer bestaat. Aangezien er bij het oplossen van problemen meerdere vertakkingen of herhalingen kunnen voorkomen, kan de volgende conclusie worden benadrukt. Elementaire algoritmische constructies (lineair, vertakt, cyclisch) zijn fundamenteel. In feite vertegenwoordigen ze de "structurele eenheid" van elke zogenaamde instructie.

Lineaire algoritmen

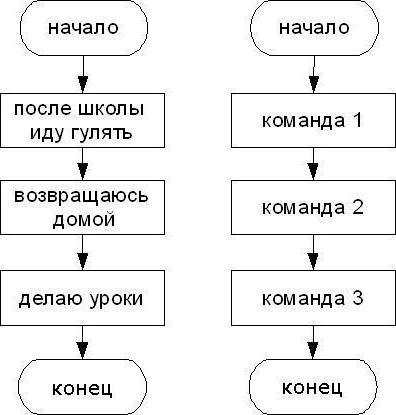
Zoals al duidelijk is uit het bovenstaande, zijn de algoritmener zijn lineaire en niet-lineaire. Laten we eens kijken naar de eerste optie. Waarom heet het zo? Alles is buitengewoon eenvoudig. Het is een feit dat alle acties die in het algoritme worden gereproduceerd een duidelijk sequentiële uitvoering hebben, alle stappen worden strikt na elkaar uitgevoerd. Dergelijke taken zijn in de regel klein en hebben een lage complexiteit.

Een voorbeeld van een lineair algoritme is het theeproces:

1. Giet water in de waterkoker.
2. Zet de waterkoker op het vuur om te koken.
3. Neem een ​​kopje.
4. Giet thee in een kopje.
5. Voeg suiker toe.
6. Giet na het koken kokend water in een kopje.
7. Pak een lepel.
8. Roer de suiker erdoor.

Het programmeren van elementaire algoritmische constructies is al moeilijk genoeg, maar als het gaat om lineaire algoritmen, is het vaak heel gemakkelijk om ze te implementeren.

Forking-algoritmen

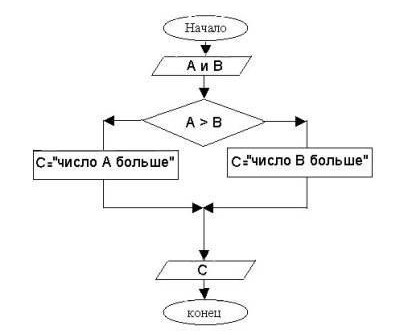
Hoe weet je of een algoritme vertakt? Het is voldoende om ervoor te zorgen dat er een keuze is uit twee of meer opties voor actie, afhankelijk van of aan de voorwaarde is voldaan of niet. Elk pad wordt een tak genoemd.

Het belangrijkste kenmerk van een vertakkingsalgoritme is het bestaan ​​van een voorwaardelijke vertakking. Het treedt op wanneer een uitdrukking wordt getest op waar of onwaar.

Meestal worden logische uitdrukkingen weergegeventekens "kleiner dan", "groter dan", "kleiner of gelijk", "groter dan of gelijk aan", "gelijk", "niet gelijk". Soms zijn er varianten waarbij de conditie aan elkaar gerelateerd is met behulp van de en (en) en of (of) commando's.

Een voorbeeld van zo'n algoritme kan de oplossing zijnvolgende taak: als de uitdrukking ((x + 3) / 1) gelijk is aan een positief getal, toon dan het resultaat op het scherm, indien negatief, informeer de gebruiker over de fout.

Het is vrij eenvoudig om de basis algoritmische constructies in de praktijk te gebruiken. Vertakking is een van de meest voorkomende oplossingsmethoden.

Deterministische of tegenlus

Tegencyclus - een cyclus die omvateen variabele die de waarde in stappen verandert. De stap wordt ingesteld door de gebruiker of geschreven door de programmeur bij het schrijven van de software. De meeste talen gebruiken de instructie for voor zo'n lus.

Om het programma vier keer twee regels te laten weergeven:

1. "Hoe gaat het met jou?"
2. "Nou dank je wel!"
3. "Hoe gaat het met jou?"
4. "Nou dank je wel!"

U moet een deterministische lus maken. Hoe ziet het eruit? Laten we de Pascal-taal gebruiken voor een beter begrip van de structuur.

1. Voor i: = 1 tot 2 doen:

- ik is de lusteller, hij bepaalt het aantal herhalingen in de lus.

2. Begin (de operator-haakjes worden geopend zodat beide zinnen de hoofdtekst van de lus vormen en samen worden herhaald).

3. Writeln (‘How are you?’):

- het woord writeln betekent de uitvoer van een zin tussen enkele aanhalingstekens.

4. Writeln ("Oké, bedankt").

5. Einde.

6. ik: = ik + 1.

Zoals u kunt zien, is het vrij eenvoudig en zelfs interessant om de algoritmische basisconstructies te gebruiken. De basisalgoritmen zijn echt algemeen bekend, zonder hen is het onmogelijk om programma's te schrijven.

Loop met postconditie

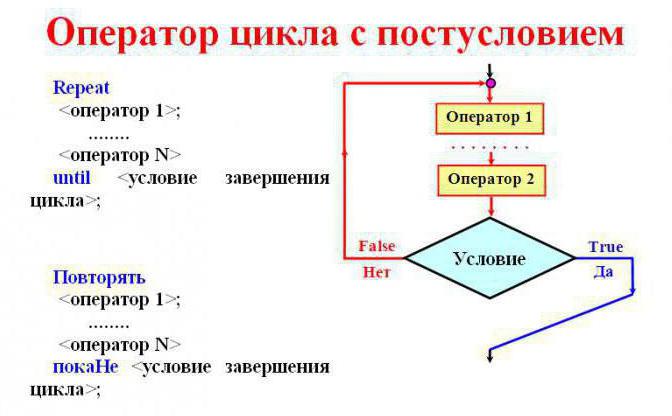
Een lus met een postconditie kan worden herhaaldeen onbeperkt aantal acties zonder er operatorhaken of samengestelde woorden in te plaatsen. Het zal zeker minstens één keer worden uitgevoerd. De lus wordt uitgevoerd terwijl de voorwaarde onwaar is. Het stopt wanneer de indicatoren correct worden. Hierop is het algoritme gebouwd. Basale algoritmische constructies van dit type werken in dit hoge tempo.

Om deze cyclus te implementeren, is de constructie nodigHerhaal A tot B. Letterlijk vertaalt het zich als "acties herhalen terwijl de voorwaarde onwaar is". Dienovereenkomstig wordt via A het herhalingsproces zelf uitgedrukt, via B-gegevens, die als resultaat de juiste waarde zouden moeten aannemen.

Loop met voorwaarde

Een lus met een postconditie is zo geconstrueerd dathet wordt in ieder geval minstens één keer uitgevoerd. Er zijn echter gevallen waarin een cyclus nodig is in het geval van een bepaalde aandoening, en als deze afwezig is, mag herhaling niet worden uitgevoerd. Anders is het resultaat onjuist. Dit is waar een preconditioneringslus wordt gebruikt. Om het te maken, heb je de "while A do B" -constructie nodig. Het eerste commando vertaalt zich letterlijk als "dag". A - conditie en B - acties die zullen worden herhaald. De hele constructie betekent: "voer, zolang de toestand waar is, acties uit".

Alle elementaire algoritmische constructies werkenalleen in bepaalde gevallen. Hoe zijn ze in een lus met een randvoorwaarde? Als u meer dan één actie moet herhalen, maar meerdere tegelijk, dan moet u samengestelde operatoren of speciale haakjes gebruiken. De lus kan heel goed mislukken als de voorwaarde niet waar is bij het invoeren ervan. Dienovereenkomstig worden de acties herhaald als deze correct zijn.

Helper-algoritme

Het helper-algoritme wordt gebruikt in andereverwerkt door alleen zijn naam op te geven. Het behoort niet tot de belangrijkste algoritmische constructies. In programmeertalen wordt zo'n actieproces een subroutine genoemd. Om het werken met de code gemakkelijker te maken en vervolgens problemen gemakkelijker op te lossen, wordt elke actie gecombineerd in één blok, dat een hulpalgoritme is. Elk van hen kan een eigen naam krijgen, zodat u er later herhaaldelijk naar kunt verwijzen.