Binaire relaties en hun eigenschappen

Een breed scala aan relaties op het voorbeeld van setsHet gaat gepaard met een groot aantal concepten, beginnend met hun definities en eindigend met een analytische analyse van paradoxen. De verscheidenheid aan concepten die in het artikel op de set worden besproken, is oneindig. Hoewel, wanneer we het over dubbele typen hebben, dit binaire relaties tussen verschillende hoeveelheden betekent. En ook tussen objecten of uitingen.

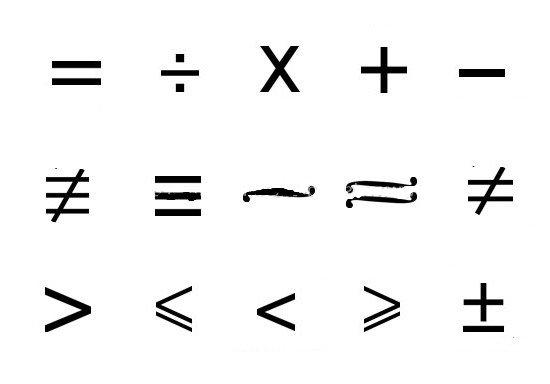
Meestal worden binaire relaties aangegevensymbool R, dat wil zeggen, als xRx voor elke waarde x uit het veld R, zo'n eigenschap reflexief wordt genoemd, waarin x en x geaccepteerde gedachtenobjecten zijn, en R dient als een teken van een of ander soort relatie tussen individuen. Tegelijkertijd, als we xRy® of yRx uitdrukken, duidt dit op een staat van symmetrie, waarbij ® een implicatieteken is, vergelijkbaar met het voegwoord "if ..., then ..." En tot slot, decodering van de inscriptie (xRy Ùy Rz) ®xRz vertelt je over een transitieve relatie, en het Ù-teken is een conjunctie.

Een binaire relatie die tegelijkertijd plaatsvindtreflexief, symmetrisch en transitief, het wordt een equivalentierelatie genoemd. De relatie f is een functie, en uit Î f en Î f volgt dat y = z. Een eenvoudige binaire functie kan gemakkelijk worden toegepast op twee eenvoudige argumenten in een bepaalde volgorde, en alleen in dit geval geeft het een betekenis die is gericht op deze twee uitdrukkingen, genomen in een bepaald geval.

Het moet gezegd worden dat f x naar y verwijst,

als f een functie is met een domein van x enzone van y-waarden. Als f echter x extrapoleert naar y, en y Í z, dan resulteert dit in f die x toont bij z. Een eenvoudig voorbeeld: als f (x) = 2x geldig is voor elk geheel getal x, dan zeggen ze dat f de ondertekende reeks van alle bekende gehele getallen toewijst aan de reeks van dezelfde gehele getallen, maar dit keer even getallen. Zoals hierboven vermeld, zijn binaire relaties die zowel reflexief, symmetrisch als transitief zijn, equivalentierelaties.

Op basis van het bovenstaande worden de equivalentierelaties van binaire relaties bepaald door de eigenschappen:

• reflexiviteit - verhouding (M ~ N);
• symmetrie - als de gelijkheid M ~ N is, dan is er N ~ M;
• transitiviteit - als twee gelijkheden M ~ N en N ~ P, dan als resultaat M ~ P.

Beschouw de gedeclareerde eigenschappen van binaire relatiesmeer gedetailleerd. Reflexiviteit is een van de kenmerken van sommige verbindingen, waarbij elk element van de onderzochte set in een bepaalde gelijkheid staat met zichzelf. Tussen de getallen a = c en a³ c zijn bijvoorbeeld reflexieve verbindingen, omdat altijd a = a, c = c, a³ a, c³ c. Tegelijkertijd is de ongelijkheidsrelatie a> c antireflexief vanwege de onmogelijkheid van het bestaan ​​van de ongelijkheid a> a. Het axioma van deze eigenschap wordt gecodeerd door tekens: aRc® aRa Ù cRc, hier betekent het symbool ® het woord "inhoudt" (of "impliceert"), en het teken Ù is de vereniging "en" (of voegwoord). Uit deze verklaring volgt dat als het oordeel aRc waar is, de uitdrukkingen aRa en cRc ook waar zijn.

Symmetrie houdt een relatie inen in het geval dat de mentale objecten worden verwisseld, dat wil zeggen, met een symmetrische relatie, leidt de permutatie van objecten niet tot een transformatie van de vorm "binaire relaties". De relatie van gelijkheid a = c is bijvoorbeeld symmetrisch vanwege de gelijkwaardigheid van de relatie c = a; het oordeel a¹c is ook hetzelfde, aangezien het overeenkomt met de verbinding met¹a.

Een transitieve verzameling is zo'n eigenschap, wantdie aan de volgende eis voldoet: y Î x, z Î y ® z Î x, waarbij ® een teken is dat de woorden vervangt: "als ..., dan ...". De formule wordt mondeling als volgt gelezen: "Als y afhangt van x, z hoort bij y, dan hangt z ook af van x."