
Istnieje kilka podstawowych algorytmów rozwiązania.zadania sortowania tablic. Jednym z najbardziej znanych jest sortowanie według wkładek. Ze względu na przejrzystość i prostotę, ale niską wydajność, metoda ta jest stosowana głównie w nauczaniu programowania. Pozwala zrozumieć podstawowe mechanizmy sortowania.
Istotą algorytmu sortowania przez wstawianie jestfakt, że wewnątrz oryginalnej tablicy tworzony jest segment uporządkowany w pożądany sposób. Każdy element jest po kolei porównywany z badaną częścią i wstawiany w odpowiednie miejsce. W ten sposób po przejściu wszystkich elementów są one ustawiane we właściwej kolejności.
Kolejność doboru elementów może być dowolna,mogą być wybrane dowolnie lub według jakiegoś algorytmu. Najczęściej stosuje się wyliczanie sekwencyjne od początku tablicy, w której powstaje uporządkowany segment.
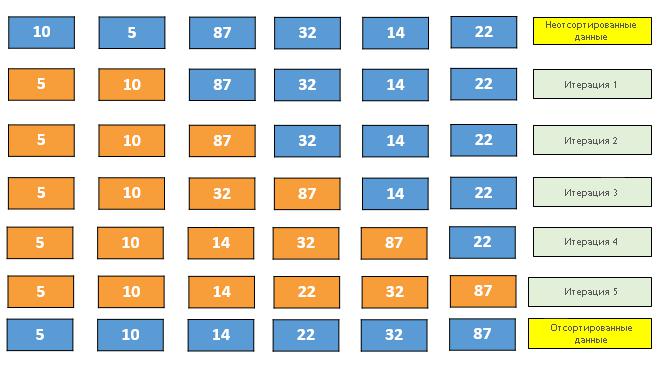
Początek rodzaju może wyglądać tak:
I tak dalej aż do końca oryginalnej tablicy.
Dla jasności warto podać przykład wykorzystania tego mechanizmu sortowania w życiu codziennym.
Weźmy na przykład portfel.W przedziale na banknoty leżą w bałaganie setki, pięćsetne i tysięczne banknoty. To bałagan, w takiej bałaganie trudno od razu znaleźć odpowiednią kartkę papieru. Tablica rachunków musi być posortowana.
Pierwszy to banknot 1000 rubli, a zaraz po nim - 100. Bierzemy setną i kładziemy ją z przodu. Trzeci z rzędu to 500 rubli, należne jej miejsce to od stu do tysiąca.
W ten sam sposób sortujemy wynikowe karty podczas gry „Głupcem”, aby ułatwić nawigację po nich.

Metoda sortowania przez wstawianie przyjmuje jako dane wejścioweoryginalna tablica do uporządkowania, funkcja porównania i, jeśli to konieczne, funkcja definiująca regułę wyliczania elementów. Najczęściej zamiast tego używany jest operator pętli regularnej.
Pierwszy element sam w sobie jest uporządkowanym zestawem, więc porównanie zaczyna się od drugiego.
Algorytm często wykorzystuje funkcję pomocniczą do zamiany dwóch wartości (swap). Wykorzystuje dodatkową zmienną tymczasową, która intensywnie wykorzystuje pamięć i nieco spowalnia kod.
Alternatywą jest przesunięcie masy grupyelementy, a następnie wstawienie obecnego na zwolnioną przestrzeń. W takim przypadku przejście do kolejnego elementu następuje, gdy porównanie zwróciło wynik dodatni, co wskazuje na prawidłową kolejność.

Konkretna implementacja zależy w dużej mierze od użytego języka programowania, jego składni i struktur.
Implementacja w klasycznym C wykorzystująca zmienną tymczasową do wymiany wartości:
int i, j, temp; dla (i = 1; i <rozmiar; i ++) { temp = tablica [i]; dla (j = i - 1; j> = 0; j--) { if (tablica [j] <temp) przerwa; tablica [j + 1] = tablica [j]; tablica [j] = temp; } }Implementacja PHP:
function insert_sort (& $ a) { for ($ i = 1; $ i <liczba ($ a); $ i ++) { $x = $a [$i]; for ($ j = $ i - 1; $ j> = 0 && $ a [$ j]> $ x; $ j--) { $a [$j + 1] = $a [$j]; } $ a [$ j + 1] = $ x; } }Tutaj najpierw wszystkie elementy, które nie spełniają warunku sortowania są przesuwane w prawo, a następnie bieżący element jest wstawiany w zwolnioną przestrzeń.
Kod Java przy użyciu pętli while:
public static void wstawianieSort (int [] arr){ for (int i = 1; i <arr.length; i ++) { int bieżElem = arr [i]; int prevKey = i - 1; while (prevKey> = 0 && arr [prevKey]> currElem) { przyp [prevKey + 1] = przyp [prevKey]; arr [prevKey] = curElem; prevKey--; } } }Ogólne znaczenie kodu pozostaje niezmienione: każdy element tablicy jest sekwencyjnie porównywany z poprzednimi i w razie potrzeby zamieniany z nimi.
Oczywiście w najlepszym przypadku przy wejściualgorytmu będzie tablicą już uporządkowaną w prawidłowy sposób. W takiej sytuacji algorytm będzie musiał po prostu sprawdzić każdy element, aby upewnić się, że jest na swoim miejscu bez wykonywania wymian. Zatem czas działania będzie bezpośrednio zależał od długości oryginalnej tablicy O (n).
W najgorszym przypadku dane wejściowe to tablica,posortowane w odwrotnej kolejności. Będzie to wymagało dużej liczby permutacji, funkcja uruchomieniowa będzie zależeć od liczby elementów do kwadratu.
Dokładną liczbę permutacji dla całkowicie nieuporządkowanej tablicy można obliczyć za pomocą wzoru:
n * (n-1) / 2, gdzie n jest długością oryginalnej tablicy. Tak więc, aby ułożyć 100 elementów we właściwej kolejności, potrzeba 4950 permutacji.
Metoda wstawiania jest bardzo wydajna przy sortowaniu małych lub częściowo uporządkowanych tablic. Jednak jego szerokie zastosowanie nie jest zalecane ze względu na dużą złożoność obliczeń.
Algorytm jest używany jako pomocnik w wielu innych, bardziej złożonych metodach sortowania.

Algorytm wstawiania należy do tzwstabilne gatunki. Oznacza to, że nie zamienia tych samych elementów, ale zachowuje ich pierwotną kolejność. Wskaźnik stabilności jest w wielu przypadkach ważny dla prawidłowego zamówienia.

Powyżej jest świetnym wizualnym przykładem sortowania tanecznego.


























