
Почетком 19. века берлински геометар Јацоб Стеинерпоставили задатак како повезати три села тако да је њихова дужина најкраћа. Након тога, овај проблем је генерализовао: потребно је пронаћи тачку на равни тако да је растојање од ње до н других тачака најмањи. У 20. веку рад на овој теми је настављен. Одлучено је да се узме неколико тачака и повеже их на такав начин да је растојање између њих најкраће. Све ово је посебан случај проблема који се проучава.
Крускалов алгоритам припада "похлепним" алгоритмима(називају се и градијент). Суштина тога је највећа исплата на сваком кораку. Похлепни алгоритми не дају увек најбоље решење проблема. Постоји теорија која показује да када се примене на одређене проблеме, они пружају оптимално решење. Ово је теорија матроида. Крускалов алгоритам припада таквим проблемима.
Разматрани алгоритам конструише оптималанжичани оквир. Проблем око тога је следећи. Даје вам се неусмерени граф без више ивица и петљи, а на скупу његових ивица дата је функција тежине в, која свакој ивици е додељује број - тежину ивице - в (е). Тежина сваког подскупа из скупа ивица одређена је збиром тежина његових ивица. Потребно је пронаћи оквир са најмањом тежином.
Крускалов алгоритам ради овако.Прво, све ивице оригиналног графикона су поређане узлазно по тежинама. У почетку скелет не садржи ивице, већ укључује све врхове графа. Након следећег корака алгоритма, једна ивица се додаје већ изграђеном делу скелета, који је распрострањена шума. Не бира се произвољно. Све ивице графикона које не припадају жичаном оквиру могу се назвати црвеним и зеленим. Врхови сваке црвене ивице налазе се у истој компоненти повезивања шуме у изградњи, а врхови зелене ивице су у различитим. Стога, ако тамо додате црвену ивицу, појавиће се циклус, а ако је зелена, компонента повезаности у шуми добијена након овог корака биће једна мање. Тако се резултирајућој конструкцији не може додати никаква црвена ивица, али се може додати било која зелена ивица да би се створила шума. Додата је и зелена ивица са минималном тежином. Резултат је најлакши оквир.
Означимо садашњу шуму Ф.Он дели скуп темена графа на подручја повезивања (њихова унија формира Ф и не секу се у паровима). Црвене ивице имају оба темена у истом делу. Део (к) је функција која за сваки врх к враћа назив дела коме к припада. Уните (к, и) је поступак који гради нову партицију, која се састоји од сједињавања к и и делова и свих осталих делова. Нека је н број ивица у графикону. Сви ови концепти укључени су у Крускалов алгоритам. Имплементација:
Поредајте све ивице графикона од 1. до н -те узлазним редоследом тежина. (аи, би су темена ивице са бројем и).
за и = 1 до н учинити.
к: = Део (аи).
и: = део (би).
Ако к није једнако и онда обједините (к, и), укључите ивицу у Ф.
Нека је Т скелет оригиналног графа конструисаног помоћу Крускал алгоритма, а С његов произвољан скелет. Морамо доказати да в (Т) не прелази в (С).
Нека је М скуп ивица С, П скуп ивицаТ. Ако С није једнако Т, онда постоји ивица оквира оквира Т која не припада С. Придружимо се ет С -у. Формира се циклус, назовимо га Ц. Уклонимо из Ц сваку ивицу ес који припадају С. Добијамо нови оквир, јер ивице, а у њему има исто толико врхова. Његова тежина не прелази в (С), будући да је в (ет) највише в (ес) на основу Крускаловог алгоритма. Понављаћемо ову операцију (замењујући ивице С ивицама Т) док не добијемо Т. Тежина сваког следећег резултујућег оквира није већа од тежине претходног, одакле следи да в (Т) није веће од в (С).
Такође, исправност Крушкаловог алгоритма следи из теорије Радо-Едмондс о матроидима.
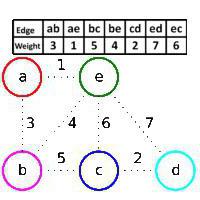
Дати графикон са теменима а, б, ц, д, е и ивицама (а,б), (а, е), (б, ц), (б, е), (ц, д), (ц, е), (д, е). Тежине ребара приказане су у табели и на слици. У почетку, шума Ф у изградњи садржи све врхове графикона и не садржи ивице. Крускалов алгоритам прво додаје ивицу (а, е), пошто има најмању тежину, а темена а и е су у различитим повезаним компонентама шуме Ф (ивица (а, е) је зелена), затим ивица ( ц, д), дакле да ова ивица има најмању тежину ивица графика која не припада Ф, а зелена је, онда се из истих разлога додаје ивица (а, б). Али ивица (б, е) се прескаче, иако има најмању тежину од преосталих ивица, јер је црвена: темена б и е припадају истој повезаној компоненти шуме Ф, односно ако додамо ивица (б, е) до Ф, добијамо циклус. Затим се додаје зелена ивица (б, ц), црвена ивица (ц, е) се прескаче, а затим д, е. Тако се ивице (а, е), (ц, д), (а, б), (б, ц) додају секвенцијално. Оптимални костур почетног графа састоји се од њих. Овако алгоритам функционише у овом случају Сликано. Пример је то показао.

На слици је приказан графикон који се састоји од две повезане компоненте. Подебљане линије приказују ивице оптималног жичаног оквира (зеленог) конструисаног помоћу Крускал алгоритма.

Горња слика приказује оригинални графикон, а доња приказује оквир минималне тежине конструисан за њу коришћењем разматраног алгоритма.
Редослед додатих ивица: (1,6); (0,3), (2,6) или (2,6), (0,3) - није важно; (3.4); (0.1), (1.6) или (1.6), (0.1) је такође индиферентно (5.6).

Крускалов алгоритам налази практичну примену, на пример, за оптимизацију полагања комуникација, путева у новим насељима насеља сваке земље, као и у другим случајевима.


























