
Свако ко је икада у животу размишљао о томеда бисте постали „информатичар“ или администратор система или једноставно повезали судбину са рачунарском технологијом, неопходно је знање о томе како се бројеви представљају у рачунарској меморији. На крају, на томе се заснивају програмски језици ниског нивоа као што је Ассемблер. Стога ћемо данас размотрити представљање бројева у рачунару и њихово смештање у меморијске ћелије.

Ако читате овај чланак, онда највероватнијевећ знате за ово, али вреди поновити. Сви подаци у личном рачунару чувају се у бинарном бројевном систему. То значи да било који број мора бити представљен у одговарајућем облику, односно који се састоји од нула и јединица.
Да бисте претворили нама познате децималне бројеве у облик разумљив рачунару, потребно је да користите алгоритам описан у наставку. Постоје и специјализовани калкулатори.
Дакле, да би се број претворио у бинарнибројевног система, морамо узети вредност коју смо изабрали и поделити је са 2. После тога добијамо резултат и остатак (0 или 1). Поделите резултат поново са 2 и сетите се остатка. Овај поступак се мора понављати док крајњи резултат такође не буде 0 или 1. Затим записујемо коначну вредност и остатке обрнутим редоследом онако како смо их добили.
Управо тако су бројеви представљени у рачунару. Било који број записује се у бинарном облику, а затим заузима меморијску ћелију.

Као што бисте већ требали знати, минимумјединица података је 1 бит. Као што смо већ сазнали, представљање бројева у рачунару је у бинарном формату. Тако ће сваки бит меморије заузети једна вредност - 1 или 0.
Ћелије се користе за складиштење великог броја.Свака таква јединица садржи до 8 битова информација. Стога можемо закључити да минимална вредност у сваком комаду меморије може бити 1 бајт или бити осмоцифрени бинарни број.
Коначно смо дошли до директног смештаја података у рачунар. Као што је већ поменуто, процесор пре свега претвара информације у бинарни формат, а тек онда их смешта у меморију.
Почећемо са најједноставнијом опцијом, са којомје представљање целих бројева у рачунару. ПЦ меморија за овај процес издваја смешно мали број ћелија - само једну. Дакле, максимум у једном слоту могу бити вредности од 0 до 11111111. Претворимо максимални број у уобичајени облик записа.
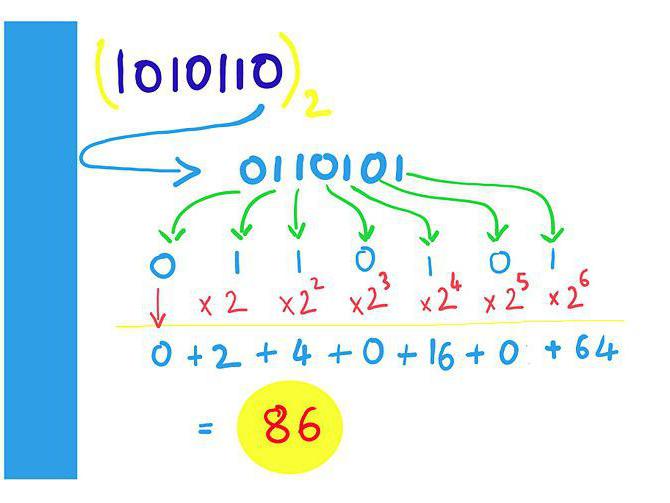
Кс = 1 × 27 + 1 × 26 + 1 × 25 + 1 × 24 + 1 × 23 + 1 × 22 + 1 × 21 + 1 × 20 = 1 × 28 - 1 = 255.
Сада то видимо у једној меморијској ћелији можекрећу се од 0 до 255. Међутим, ово се односи само на негативне целе бројеве. Ако рачунар треба да напише негативну вредност, ствари иду мало другачије.

Сада да видимо како то идепредстављање бројева у рачунару ако су негативни. Да би се прилагодила вредност мања од нуле, додељују се две меморијске ћелије или 16 битова информација. У овом случају, 15 иде испод самог броја, а први (крајњи леви) бит је дат под одговарајућим знаком.
Ако је цифра негативна, напишите „1“, ако је позитивна, онда „0“. Ради лакшег памћења можете повући следећу аналогију: ако постоји знак, ставите 1, ако није, онда ништа (0).
Преосталих 15 битова информација додељује се броју.Слично претходном случају, у њих се може сместити највише петнаест јединица. Вреди напоменути да се бележење негативних и позитивних бројева значајно разликује једно од другог.
Да стане на 2 меморијске локацијевредност већа од или једнака нули, користи се такозвани директни код. Ова операција се изводи на исти начин као што је описано, а максимум А = 32766, ако користите систем децималног броја. Одмах бих приметио да се у овом случају „0“ односи на позитивне.
Приказивање целих бројева у рачунарској меморији нијеје тако тежак задатак. Ипак постаје мало компликованије када су у питању негативне вредности. За писање броја мањег од нуле користи се комплементарни код.
Да би га добила, машина врши бројне помоћне операције.
Дајмо илустративан пример.Претпоставимо да имамо број Кс = - 131. Прво, добијамо његов модул | Кс | = 131. Затим га преведемо у бинарни систем и запишемо у 16 ћелија. Добијамо Кс = 0000000010000011. Након инвертовања, Кс = 1111111101111100. Додајте му „1“ и добићете обрнути код Кс = 1111111101111101. Да бисте писали у 16-битну меморијску ћелију, минимални број је Кс = - (215) = - 32767.
Као што видите, приказ стварних бројева урачунар није толико тежак. Међутим, овај опсег можда није довољан за већину операција. Због тога, да би примио велике бројеве, рачунар додељује 4 ћелије или 32 бита из меморије.
Процес снимања се нимало не разликује од горе представљеног. Дакле, само ћемо навести опсег бројева који се могу сачувати у овом типу.
КсСвинг= 2 147 483 647.
Ксмин= - 2 147 483 648.

У већини случајева ове вредности су довољне за снимање и извођење операција података.
Представљање реалних бројева у рачунаруима предности и недостатке. С једне стране, ова техника олакшава извођење операција између целобројних вредности, што знатно убрзава процесор. С друге стране, овај опсег није довољан за решавање већине проблема из економије, физике, аритметике и других наука. Стога ћемо сада размотрити још једну технику за супермагнитуде.
Ово је последње о чему треба да знатепредстављање бројева у рачунару. Будући да приликом писања разломака постоји проблем одређивања положаја зареза у њима, рачунар користи експоненцијални облик за постављање таквих бројева.
Било који број може бити представљен у следећем облику Кс = м * пн... Где је м мантиса броја, п је основа бројевног система, а н је редослед броја.
Да би се стандардизовало снимање бројева са покретном зарезом, користи се следећи услов према којем модул мантисе мора бити већи или једнак 1 / н и мањи од 1.
Дајмо нам број 666,66. Доведимо је у експоненцијални облик. Испада Кс = 0,66666 * 103... П = 10 и н = 3.
Вредности са покретном зарезом обично се чувају у 4 или 8 бајтова (32 или 64 бита). У првом случају то се назива нормалним бројем прецизности, а у другом двоструком прецизношћу.
Од 4 бајта додељена за чување цифара, 1 (8битс) даје се за податке о редоследу и његовом знаку, а 3 бајта (24 бита) се користе за чување мантисе и њеног знака према истим принципима као и за целобројне вредности. Знајући ово, можемо извршити једноставне прорачуне.
Максимална вредност н = 11111112 = 12710... На основу њега можемо добити максималну величину броја који се може сачувати у меморији рачунара. Кс = 2127... Сада можемо израчунати максимално могућу мантису. Биће једнако 223 - 1 ≥ 223 = 2(10 × 2,3) ≥ 10002,3 = 10(3 × 2,3) ≥ 107... Као резултат, добили смо приближну вредност.
Ако сада комбинујемо оба израчунавања, добићемо вредност која се може записати без губитка у 4 бајта меморије. Биће једнако Кс = 1.701411 * 1038... Остале слике су одбачене, јер управо то омогућава тачност снимања.

Пошто су сви прорачуни заказани иобјашњено у претходном пасусу, овде ћемо све објаснити врло кратко. За бројеве двоструке прецизности обично се додељује 11 битова за ред и његов знак, као и 53 бита за мантису.
П = 11111111112 = 102310.
М = 252 -1 = 2(10 * 5,2) = 10005.2 = 1015.6... Заокружите и добијете максималан број Кс = 21023 тачно на „м“.
Надамо се да ће вам информације које смо пружили о представљању целих бројева и стварних бројева у рачунару бити корисне за вас на тренингу и биће бар мало јасније од онога што се обично пише у уџбеницима.


























