
Opiskellessaan fysiikkaa 10. luokassa otetaan huomioon dipolien aihe. Mitä tämä käsite tarkoittaa ja mitä kaavoja käytetään sen laskemiseen?
Jos sijoitamme dipolin homogeenisen tilaansähkökenttä, voit kuvitella sen voimajoukoina. Dipoli on järjestelmä, jossa on kaksi parametreillä identtistä varausta, mutta ne ovat vastakkaisia pisteitä. Lisäksi niiden välinen etäisyys on paljon pienempi kuin etäisyys mihin tahansa dipolikentän pisteeseen. Dipolimomentin käsitettä tutkitaan elektrodynamiikan koulukurssilla (luokka 10).
Dipoli-akseli on suora viiva, joka kulkee läpimolempien maksujen pistettä. Dipolivarsi on vektori, joka yhdistää varauksen ja on suunnattu negatiivisesti varautuneista hiukkasista positiivisesti varautuneisiin hiukkasiin. Sähköiselle dipolille on ominaista sellaisen tilan esiintyminen kuin dipoli tai sähkömomentit.
Määritelmän mukaan dipolimomentti onvektori, joka on numeerisesti yhtä suuri kuin dipolivaraus sen olkapäässä. Lisäksi se on linjassa dipolivarren kanssa. Kun voimien summa on yhtä suuri kuin nolla, lasketaan hetken arvo. Dipolimomentin ja sähkökentän suunnan väliselle kulmalle on tunnusomaista mekaanisen momentin läsnäolo.

Usein ihmisten on vaikea tehdä laskelmiamoduuli, joka vaikuttaa dipolin rakenteeseen. Tässä on tarpeen ottaa huomioon kulman "Alpha" laskemisen erityispiirteet. Tiedetään, että dipoli poikkeaa tasapainotetusta asennosta. Mutta itse dipolimomentti erottuu palauttavasta luonteesta, koska se on taipuvainen olemaan liikkeessä.
Sijoittamalla tämä dipolihetki keskiviikkonaepähomogeeninen sähkökenttä aiheuttaa väistämättä voiman vaikutuksen. Tällaisessa ympäristössä voimien summan indikaattorit eivät ole nollia. Tästä johtuen dipolimomenttiin vaikuttavat voimat, joilla on pistemerkki. Dipolivarsi on paljon pienempi.
Kaava voidaan kirjoittaa seuraavasti: F = q (E2 - E1) = qdE, missä d on sähkökentän ero.
Tarkastellaan aihetta edelleen.Sähkökentän ominaispiirteiden määrittämiseksi on tehtävä useita laskelmia, jos se syntyy varausjärjestelmän avulla ja lokalisoituu pieneen tilaan. Esimerkin tarjoavat atomit ja molekyylit, jotka sisältävät koostumukseltaan sähköisesti varautuneita ytimiä ja elektroneja.
Jos haluat etsiä kenttää etäisyydellä,suurempia kuin hiukkasten pinta-alan koot, käytämme useita tarkkoja kaavoja, jotka ovat erittäin monimutkaisia. On mahdollista käyttää yksinkertaisempia likimääräisiä lausekkeita. Oletetaan, että pistejoukot varauksia qettä... Ne sijaitsevat pienessä tilassa.
Ominaislaskelmien suorittamiseksimikä kentällä on, järjestelmän kaikkien maksujen yhdistäminen on sallittua. Tällaista järjestelmää pidetään pistemaksuna Q. Suuruuden arvot ovat alkuperäisessä järjestelmässä olevien varausten summa.

Kuvittele, että latauksen sijainti ilmoitetaan missä tahansa latausjärjestelmässä qettä... Kun teet sijaintimuutoksia,jos sillä on pienellä alueella ilmaistuja rajoja, tällainen vaikutus on merkityksetön, melkein näkymätön kentälle tarkastelukohteessa. Sähkökentän voimakkuuden ja potentiaalin likiarvon rajoissa määritelmät tehdään perinteisiä kaavoja käyttäen.
Nollalla järjestelmän koko latauksen,ilmoitetun likiarvon parametrit näyttävät karkeilta. Tämä johtaa johtopäätökseen, että sähkökenttä yksinkertaisesti puuttuu. Jos on tarpeen saada tarkempi arvio, he keräävät henkisesti erilliset ryhmät tarkasteltavan järjestelmän positiivisista ja negatiivisista varauksista.
Jos heidän "keskusten" sukulainen siirtyytoiset, kentän parametrit tällaisessa järjestelmässä voidaan kuvata kentän muodossa, jolla on kaksi pistelatausta, yhtä suuret ja vastakkaiset. On huomattava, että he ovat puolueellisia muihin nähden. Jotta latausjärjestelmä voidaan kuvata tarkemmin tämän likiarvon parametrien suhteen, on tarpeen tutkia dipolin ominaisuuksia sähkökentässä.
Palataan takaisin määritelmään.Sähköinen dipoli on määritelmä järjestelmälle, jolla on kaksi pistevarausta. Heillä on sama koko ja vastakkaiset merkit. Lisäksi tällaiset merkit sijaitsevat pienillä etäisyyksillä muihin merkkeihin nähden.
Voit laskea prosessin ominaisuuden, joka luodaan dipolin avulla, ja sitä edustaa kaksi pistevarausta: + q ja −q, ja ne sijaitsevat etäisyydellä suhteessa muihin.

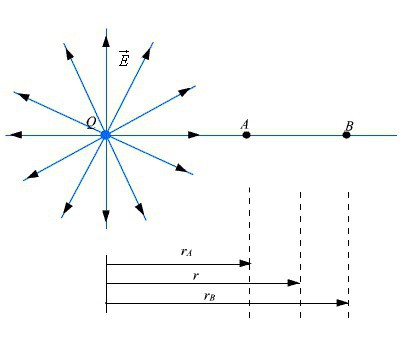
Aloitetaan laskemalla potentiaali jajännitys, joka dipolilla on aksiaalisella pinnallaan. Tämä on suora viiva, joka kulkee kahden latauksen välillä. Jos piste A sijaitsee etäisyydellä, joka on yhtä suuri kuin r suhteessa dipolin keskiosaan, ja jos se on r >> a, kenttäpotentiaalin päällekkäisyyden periaatteen mukaisesti tietyssä pisteessä on järkevää käyttää lauseketta sähköisen dipolin parametrien laskemiseen.
Jännitysvektorin arvo lasketaan päällekkäisyyden periaatteen mukaisesti.
Kentän voimakkuuden laskemiseen käytetään potentiaalin ja kentän voimakkuuden välisen suhteen käsitettä:
Ekanssa = −Δφ / Δx.
Tällaisissa olosuhteissa intensiteettivektorin suunta ilmoitetaan pituussuunnassa dipolin akseliin nähden. Sen moduulin laskemiseksi sovelletaan vakiokaavaa.
On pidettävä mielessä, että kenttä heikkeneesähködipoli tapahtuu nopeammin kuin se kokee pistelatauksen. Dipolikentän potentiaalin pieneneminen tapahtuu kääntäen verrannollisessa suunnassa etäisyyden neliöön nähden ja kentän voimakkuus - kääntäen verrannollisessa suunnassa etäisyyden kuutioon nähden.
Käyttämällä samanlaista, mutta hankalampaaMenetelmät, dipolin potentiaalin ja kentän voimakkuuden parametrit löytyvät mielivaltaisista pisteistä, joiden sijaintiparametrit määritetään käyttämällä sellaista laskentamenetelmää napakoordinaatteina: etäisyys sähköisen dipolin keskipisteeseen (r) ja kulma (θ).
Jännitysvektorin E käsite on jaettu kahteen pisteeseen:

Tämä kunkin komponentin hajoaminen on suunnatturadan varrella muutos, joka tapahtuu kaikilla havaintopisteen koordinaateilla. Se löytyy suhteesta, joka yhdistää kentänvoimakkuuden indikaattorit mahdollisiin muutoksiin.
Vektorikomponentin löytäminen kentänvoimakkuudesta on tärkeää selvittää suhteen luonne potentiaalisissa muutoksissa, jotka tapahtuvat havaintopisteen siirtymisen vuoksi vektorien suuntaan.
Tätä toimenpidettä suoritettaessa on tärkeää ottaa huomioon, että arvon ilmaisu pienellä kohtisuoralla siirtymällä määritetään muuttamalla kulmaa: Δl = rAθ.
Tämän kenttäkomponentin suuruusparametrit ovat samat.
Saatuaan suhde on mahdollista määrittää sähköisen dipolin kenttä mielivaltaisessa pisteessä kuvan rakentamiseksi tämän kentän voimajohdoilla.
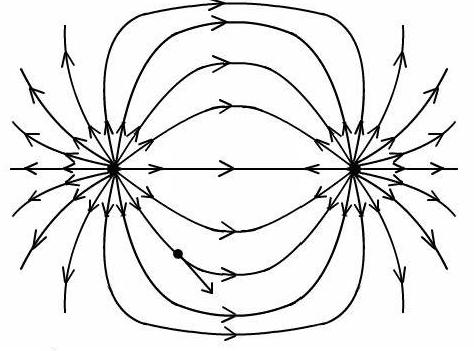
On tärkeää ottaa huomioon, että kaikki kaavat dipolin potentiaalin ja kenttävoimakkuuden määrittämiseksi toimivat vain yhden dipolipanoksen määrien ja niiden välisen etäisyyden tulolla.
Kuvatun työn otsikko on täydellinen kuvaus sähköisten ominaisuuksien tyypistä. Sitä kutsutaan "järjestelmän dipolimomentiksi".
Dipolin määritelmän mukaan, joka onPistevarausten järjestelmästä voidaan saada selville, että sille on tunnusomaista aksiaalisen symmetrian esiintyminen, kun akseli on suora viiva, joka kulkee useiden varausten läpi.
Määritä dipolin täysi ominaisuusosoittavat myös akselin suunnan. Laskennan helpottamiseksi voit määrittää dipolimomentin vektorin. Sen arvo on yhtä suuri kuin dipolimomentin arvo, ja suuntavektori eroaa sen ja dipoli-akselin sattumasta. Joten, p = qa, jos a on vektorin suunta, joka yhdistää dipolin negatiiviset ja positiiviset varaukset.

Tällaisen dipoliominaisuuden käyttö on mukavaa jamahdollistaa useimmissa tapauksissa kaavan yksinkertaistamisen ja sen näyttämisen vektorina. Dipolikentän potentiaalin kuvaus mielivaltaisen suunnan pisteessä kirjoitetaan vektorin muodossa.
Johdanto käsitteisiin, kuten vektoridipolin ja sen dipolimomentin ominaisuus voidaan suorittaa käyttämällä yksinkertaistettua mallia - pistemaksu yhtenäisellä kentällä, joka sisältää varausjärjestelmän, jonka geometrisia mittoja ei ole tarpeen ottaa huomioon, mutta on tärkeää tietää dipolimomentti. Tämä on edellytys laskelmien suorittamiselle.
Dipolin käyttäytymistä voidaan tarkastella esimerkissätällaisessa tilanteessa. Kahden pistemäärän sijainnilla on kiinteä etäisyys toisiinsa nähden. Ne asetettiin yhtenäiseen sähkökentän dipolitilaan. Havaitsi prosessin. Fysiikan (elektrodynamiikka) oppitunneilla he tarkastelevat tätä käsitettä yksityiskohtaisesti. Kentästä lataukseen voimien toiminta suoritetaan:
F = ± qE
Ne ovat yhtä suuria ja päinvastaisiasuunnan luonteen mukaan. Dipoliin vaikuttavan kokonaisvoiman indikaattori on nolla. Koska tällaisella voimalla on vaikutusta eri pisteisiin, kokonaismomentin indikaattori on:
M = Fa sin a = qEa sin a = pE syn a
α: lle, joka on vektorien yhdistävä kulmadipolimomentin kenttävoimakkuudet ja vektorit. Voimamomentin läsnäolon vuoksi järjestelmän dipolimomentilla on taipumus palata sähkökentän voimakkuusvektorin suuntiin.
Sähköinen dipoli on käsite, joka on tärkeää ymmärtää selvästi. Voit lukea siitä lisää Internetistä. Sitä voidaan opiskella myös fysiikan oppitunneilla koulussa 10. luokassa, josta puhuimme edellä.


























