
Merkittävä määrä matemaattisia ongelmialiittyy havaitsemiseen, joka on jakautunut epätasaisesti informaatiotilassa. Puhumme maantieteellisen suuntautumisen tietojärjestelmistä, koska juuri niissä on mahdollista mitata tarvittavat arvot tietyissä kohdissa. Näiden ongelmien ratkaisemiseksi käytetään usein yhtä tai toista interpolointimenetelmää.

Interpolointi on laskentaarvojen väliarvot käytettävissä olevan erillisen arvojoukon mukaisesti. Yleisimmät interpolointimenetelmät ovat: painotettujen etäisyyksien menetelmä, trendipinta ja kriging.
Katsotaanpa lähemmin ensimmäistä menetelmää, sen ydintäkoostuu pisteiden vaikutuksesta, jotka ovat lähempänä arvioitua verrattuna edelleen sijaitseviin pisteisiin. Tällaista interpolointimenetelmää käytettäessä on välttämätöntä valita tietystä naapuruston tietystä topografiasta tietty piste, jolla on siihen suurin vaikutus. Tämä valitsee suurimman hakusäteen tai tiettyjen pisteiden lähellä olevien pisteiden määrän. Seuraavaksi paino asetetaan korkeudelle kussakin tietyssä pisteessä laskettuna etäisyydestä tästä pisteestä. Vain tällä tavoin voidaan saavuttaa lähimpien pisteiden suurempi osuus interpoloidussa korkeudessa verrattuna pisteisiin, jotka ovat kauempana tietystä etäisyydestä.
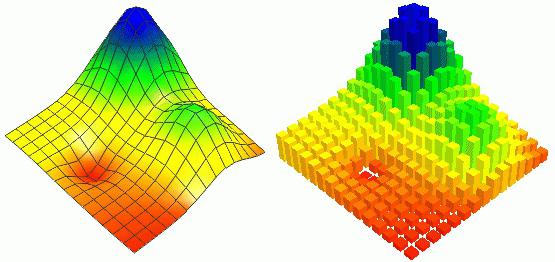

On toinenkin määrittelytyökaluerityiset kohdat - neliöllisen interpoloinnin menetelmä, jonka ydin on korvata jokin funktio tietyllä aikavälillä neliöllisellä parabolalla. Lisäksi sen ekstremumi lasketaan analyyttisesti. Arvioidun sijaintinsa (minimi tai maksimiarvo) jälkeen on tarpeen asettaa tietty arvoalue, jonka jälkeen ratkaisun etsiminen jatkuu. Toistamalla tämä toimenpide uudelleen, käyttämällä iteratiivista menettelyä, voidaan tarkentaa tämän yhtälön arvo tulokseksi ongelmanilmaisussa määritellyllä tarkkuudella.


























