
Au début du XIXe siècle, un géomètre de Berlin, Jacob SteinerIl a confié la tâche de relier les trois villages afin que leur longueur soit la plus courte. Par la suite, il a généralisé ce problème: il faut trouver un point dans l'avion de telle sorte que la distance de celui-ci à n autres points soit la plus petite. Au XXe siècle, les travaux se sont poursuivis sur ce sujet. Il a été décidé de prendre plusieurs points et de les relier afin que la distance entre eux soit la plus courte. Il s'agit là d'un cas particulier du problème étudié.
L'algorithme de Kruskal fait référence aux gourmands(ils sont aussi appelés dégradés). L'essence de ceux-ci est le plus grand gain à chaque étape. Les algorithmes "gourmands" ne donnent pas toujours la meilleure solution au problème. Il existe une théorie montrant que lorsqu'ils sont appliqués à certaines tâches, ils fournissent une solution optimale. Telle est la théorie des matroïdes. L'algorithme Kraskal fait référence à de tels problèmes.
L'algorithme considéré construit l'optimalcadre graphique. Le problème est le suivant. Un graphique non orienté est donné sans plusieurs arêtes et boucles, et une fonction de pondération w est affectée sur l'ensemble de ses arêtes, qui attribue à chaque arête e un nombre - le poids de l'arête - w (e). Le poids de chaque sous-ensemble de l'ensemble d'arêtes est déterminé par la somme des poids de ses arêtes. Il est nécessaire de trouver le cadre du plus petit poids.
L'algorithme Kraskal fonctionne comme ceci.Tout d'abord, tous les bords du graphique d'origine sont classés par ordre croissant de poids. Initialement, le cadre ne contient aucune arête, mais inclut tous les sommets du graphique. Après l'étape suivante de l'algorithme, une arête est ajoutée à la partie déjà construite du cadre, qui est la forêt s'étendant. Il n'est pas choisi arbitrairement. Tous les bords du graphique qui n'appartiennent pas au cadre peuvent être appelés rouge et vert. Les sommets de chaque arête rouge sont dans un composant connexe de la forêt en construction et les sommets verts sont différents. Par conséquent, si vous y ajoutez un bord rouge, un cycle apparaît, et s'il est vert, dans la forêt obtenue après cette étape, les composants connectés seront moins d'un. Ainsi, pas une seule bordure rouge ne peut être ajoutée à la construction résultante, mais une bordure verte peut être ajoutée pour obtenir une forêt. Et une côte verte avec un poids minimal est ajoutée. Le résultat est une monture du plus petit poids.
Indique la forêt actuelle F.Il divise l'ensemble des sommets du graphe en aires connectées (leur union forme F, et elles ne se coupent pas par paires). Aux bords rouges, les deux pics se trouvent en une seule partie. La partie (x) est une fonction qui, pour chaque sommet x, renvoie le nom de la partie à laquelle appartient x. Unite (x, y) est une procédure qui crée une nouvelle partition, constituée de l'union des parties x et y et de toutes les autres parties. Soit n le nombre d'arêtes du graphe. Tous ces concepts sont inclus dans l'algorithme de Kraskal. Réalisation:
Triez tous les bords du graphique du 1er au nième par ordre croissant de poids. (ai, bi sont les sommets de l'arête avec le numéro i).
pour i = 1 à n do.
x: = partie (ai).
y: = partie (bi).
Si x n'est pas égal à y alors Unir (x, y), inclure dans l'arête F le nombre i.
Soit T le cadre du graphe original construit en utilisant l'algorithme de Kruskal, et S son cadre arbitraire. Il est nécessaire de prouver que w (T) ne dépasse pas w (S).
Soit M l'ensemble des arêtes S, P l'ensemble des arêtesT. Si S n'est pas égal à T, alors il y a une arête et du squelette T qui n'appartient pas à S. Nous attachons et à S. Nous formons un cycle, appelons-le C. Nous supprimons de C toutes les arêtes appartenant à S. Nous obtenons un nouveau squelette, car il y a aussi des arêtes et il y a autant de pics. Son poids ne dépasse pas w (S), car w (et) n'est pas supérieur à w (es) grâce à l'algorithme de Kraskal. Cette opération (remplacement des bords de S par les bords de T) sera répétée jusqu'à obtenir T. Le poids de chaque trame suivante obtenue n'est pas supérieur au poids de la précédente, ce qui implique que w (T) n'est pas supérieur à w (S).
La justesse de l'algorithme de Kruskal découle également du théorème de Rado-Edmonds sur les matroïdes.
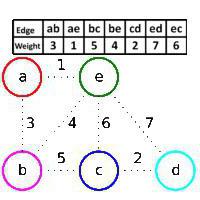
Un graphique avec les sommets a, b, c, d, e et les arêtes (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Les poids des côtes sont indiqués dans le tableau et sur la figure. Initialement, la forêt en construction F contient tous les sommets du graphe et ne contient aucune arête. L'algorithme de Kraskal ajoutera d'abord l'arête (a, e), car elle a le plus petit poids, et les sommets a et e sont dans différentes composantes de la forêt F (l'arête (a, e) est verte), puis l'arête (c, d), donc que cette arête a le plus petit poids des arêtes du graphe qui n'appartiennent pas à F, et qu'elle est verte, alors, pour les mêmes raisons, l'arête (a, b) est ajoutée. Mais l'arête (b, e) est sautée, bien qu'elle ait le plus petit poids des arêtes restantes, car elle est rouge: les sommets b et e appartiennent à la même composante connectée de la forêt F, c'est-à-dire que si on ajoute l'arête (b, e) à F, alors cycle. Ensuite, un bord vert (b, c) est ajouté, un bord rouge (c, e) est ignoré, puis d, e. Ainsi, les bords (a, e), (c, d), (a, b), (b, c) sont ajoutés séquentiellement. Le cadre optimal du graphique d'origine est composé de nihers. C'est ainsi que l'algorithme fonctionne dans ce cas. Kraskala. Un exemple est montré.

La figure montre un graphique composé de deux composants connectés. Les lignes en gras montrent les bords du cadre optimal (vert) construit à l'aide de l'algorithme de Kraskal.

Le graphique du haut montre le graphique d'origine et celui du bas montre le cadre de poids minimum construit pour lui en utilisant l'algorithme en question.
La séquence de côtes ajoutées: (1,6); (0,3), (2,6) ou (2,6), (0,3) - peu importe; (3.4); (0,1), (1,6) ou (1,6), (0,1) est également indifférent (5,6).

L'algorithme de Kraskal trouve une application pratique, par exemple, pour optimiser la pose des communications, les routes dans les nouveaux microdistricts de colonies dans chaque pays, ainsi que dans d'autres cas.


























