
Jacob Steiner, geometra berlinese dell'inizio del XIX secoloimpostare il compito di collegare tre villaggi in modo che la loro lunghezza fosse la più breve. Successivamente, ha generalizzato questo problema: è necessario trovare un punto sul piano in modo che la distanza da esso a n altri punti sia la più piccola. Nel 20 ° secolo, il lavoro è continuato su questo argomento. Si è deciso di prendere diversi punti e collegarli in modo tale che la distanza tra loro fosse la più breve. Tutto questo è un caso speciale del problema in esame.
L'algoritmo di Kruskal appartiene agli algoritmi "greedy"(sono anche chiamati gradiente). L'essenza di tale è il più grande guadagno ad ogni passo. Gli algoritmi avidi non sempre danno la migliore soluzione al problema. C'è una teoria che mostra che quando applicati a problemi specifici, forniscono una soluzione ottimale. Questa è la teoria dei matroidi. L'algoritmo di Kruskal appartiene a tali problemi.
L'algoritmo considerato costruisce l'ottimografico wireframe. Il problema al riguardo è il seguente. Ti viene dato un grafo non orientato senza più archi e loop, e sull'insieme dei suoi archi viene data una funzione peso w, che assegna a ciascun arco e un numero - il peso dell'arco - w (e). Il peso di ogni sottoinsieme dell'insieme degli archi è determinato dalla somma dei pesi dei suoi archi. È necessario trovare il telaio con il peso minore.
L'algoritmo di Kruskal funziona così.Innanzitutto, tutti i bordi del grafo originale sono disposti in ordine crescente di pesi. Inizialmente, lo scheletro non contiene alcuno spigolo, ma include tutti i vertici del grafico. Dopo il passaggio successivo dell'algoritmo, viene aggiunto un bordo alla parte già costruita dello scheletro, che è una foresta estesa. Non è scelto arbitrariamente. Tutti i bordi del grafico che non appartengono al wireframe possono essere chiamati rosso e verde. I vertici di ciascun bordo rosso sono nella stessa componente di connettività della foresta in costruzione e i vertici del bordo verde sono in diversi. Pertanto, se aggiungi un bordo rosso lì, appare un ciclo e, se è verde, il componente di connessione nella foresta ottenuto dopo questo passaggio sarà uno in meno. Pertanto, nessun bordo rosso può essere aggiunto alla costruzione risultante, ma è possibile aggiungere qualsiasi bordo verde per creare una foresta. E viene aggiunto un bordo verde con un peso minimo. Il risultato è il telaio più leggero.
Indichiamo l'attuale foresta F.Divide l'insieme dei vertici del grafo in aree di connettività (la loro unione forma F e non si intersecano a coppie). I bordi rossi hanno entrambi i vertici nella stessa parte. Parte (x) è una funzione che, per ogni vertice x, restituisce il nome della parte a cui x appartiene. Unite (x, y) è una procedura che costruisce una nuova partizione, costituita dall'unione delle parti x e y e di tutte le altre parti. Sia n il numero di archi nel grafico. Tutti questi concetti sono inclusi nell'algoritmo di Kruskal. Implementazione:
Disponi tutti i bordi del grafico dal 1° all'ennesimo in ordine di peso crescente. (ai, bi sono i vertici dello spigolo con numero i).
per i = 1 a n do.
x: = Parte (ai).
y: = Parte (bi).
Se x non è uguale a y, allora Unite (x, y), includi il bordo i in F.
Sia T lo scheletro del grafo originale costruito usando l'algoritmo di Kruskal e S il suo scheletro arbitrario. Dobbiamo dimostrare che w (T) non supera w (S).
Sia M l'insieme degli archi S, P l'insieme degli archiT. Se S non è uguale a T, allora c'è un arco et del frame T che non appartiene a S. Attacciamo et a S. Si forma un ciclo, chiamiamolo C. Togliamo da C qualsiasi arco es appartenente a S. Otteniamo una nuova cornice, perché i bordi, e ci sono altrettante cime in essa. Il suo peso non supera w (S), poiché w (et) è al massimo w (es) in virtù dell'algoritmo di Kruskal. Ripeteremo questa operazione (sostituendo i bordi S con i bordi T) fino ad ottenere T. Il peso di ogni frame risultante successivo non è maggiore del peso del precedente, da cui segue che w (T) non è maggiore di w (S).
Inoltre, la correttezza dell'algoritmo di Kruskal deriva dal teorema di Rado-Edmonds sui matroidi.
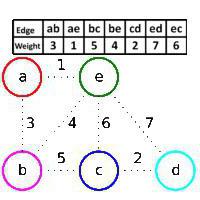
Dato un grafo con vertici a, b, c, d, e e archi (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). I pesi delle centine sono riportati in tabella e in figura. Inizialmente, la foresta F in costruzione contiene tutti i vertici del grafo e non contiene alcuno spigolo. L'algoritmo di Kruskal aggiunge prima il bordo (a, e), poiché ha il peso più piccolo, e i vertici a ed e sono in diverse componenti connesse della foresta F (il bordo (a, e) è verde), quindi il bordo ( c, d), quindi che questo arco ha il peso minimo degli archi del grafo che non appartiene ad F, ed è verde, allora si aggiunge l'arco (a, b) per gli stessi motivi. Ma lo spigolo (b, e) viene saltato, anche se ha il peso minore dei restanti spigoli, perché è rosso: i vertici b ed e appartengono alla stessa componente connessa della foresta F, cioè se sommiamo il bordo (b, e) a F, otteniamo ciclo. Quindi viene aggiunto un bordo verde (b, c), un bordo rosso (c, e) viene saltato e quindi d, e. Pertanto, gli spigoli (a, e), (c, d), (a, b), (b, c) vengono aggiunti in sequenza. Lo scheletro ottimale del grafico iniziale è costituito da loro. Ecco come funziona l'algoritmo in questo caso Dipinto. Un esempio lo ha dimostrato.

La figura mostra un grafico costituito da due componenti collegati. Le linee in grassetto mostrano i bordi del wireframe ottimale (verde) costruito utilizzando l'algoritmo Kruskal.

La figura superiore mostra il grafico originale e quella inferiore mostra il framework di peso minimo costruito per esso utilizzando l'algoritmo considerato.
La sequenza dei bordi aggiunti: (1,6); (0.3), (2.6) o (2.6), (0.3) - non importa; (3.4); (0.1), (1.6) o (1.6), (0.1) è anche indifferente (5.6).

L'algoritmo di Kruskal trova applicazione pratica, ad esempio, per ottimizzare la posa di comunicazioni, strade in nuovi quartieri di insediamenti di ogni paese, così come in altri casi.


























