
Ora ci concentreremo sull'ottica geometrica.Questa sezione dedica molto tempo a un oggetto come una lente. Dopotutto, può essere diverso. In questo caso, la formula per una lente sottile è la stessa per tutti i casi. Hai solo bisogno di sapere come applicarlo correttamente.

È sempre un corpo trasparente ai raggi di luce, che ha una forma speciale. L'aspetto dell'oggetto è dettato da due superfici sferiche. Uno di loro può essere sostituito con uno piatto.
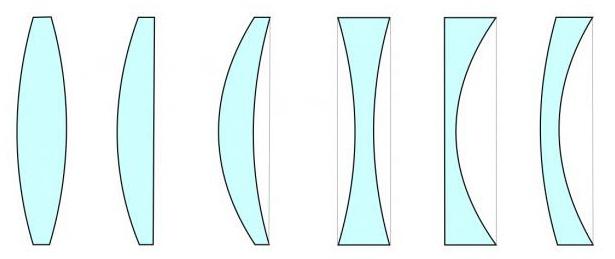
Inoltre, la lente può essere più spessa al centro oi bordi. Nel primo caso, sarà chiamato convesso, nel secondo - concavo. Inoltre, a seconda di come si combinano superfici concave, convesse e piatte, anche le lenti possono essere diverse. Vale a dire: biconvesso e biconcava, piano-convesso e piano-concavo, convesso-concavo e concavo-convesso.
In condizioni normali, questi oggetti vengono utilizzati inaria. Sono costituiti da una sostanza la cui densità ottica è maggiore di quella dell'aria. Pertanto, una lente convessa si raccoglierà e una lente concava si diffonderà.
Prima di parlare formula di lenti sottili, devi decidere i concetti di base. Devi assolutamente conoscerli. Perché saranno costantemente affrontati da vari compiti.
L'asse ottico principale è una linea retta.Viene disegnato attraverso il centro di entrambe le superfici sferiche e definisce dove si trova il centro della lente. Ci sono anche assi ottici aggiuntivi. Sono disegnati attraverso il punto che è il centro della lente, ma non contengono i centri delle superfici sferiche.
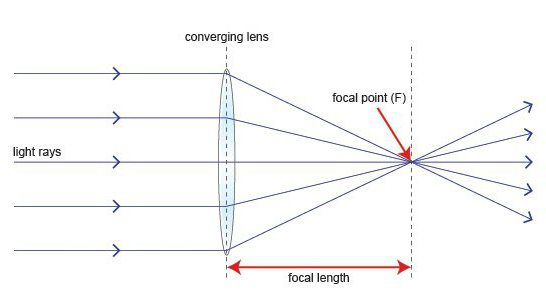
Nella formula per una lente sottile, c'è un valore che determina la sua lunghezza focale. Quindi, il fuoco è un punto sull'asse ottico principale. Interseca i raggi che corrono paralleli all'asse specificato.
Inoltre, ci sono sempre due trucchi per ogni lente sottile. Si trovano su entrambi i lati delle sue superfici. Entrambi i focus sono validi per il collezionista. Quello che sparge è immaginario.
La distanza dall'obiettivo al punto focale è la lunghezza focale (lettera F). Inoltre, il suo valore può essere positivo (nel caso di raccolta) o negativo (per dispersione).
Un'altra caratteristica è associata alla lunghezza focale: potenza ottica. È consuetudine denotarlo D. Il suo valore è sempre il reciproco del focus, cioè D = 1 /F. La potenza ottica è misurata in diottrie (abbreviate, diottrie).
Oltre alla lunghezza focale già indicata, dovrai conoscere diverse distanze e dimensioni. Sono uguali per tutti i tipi di lenti e sono presentati nella tabella.
| designazione | nome |
| d | distanza dell'oggetto |
| h | altezza del soggetto studiato |
| f | distanza dell'immagine |
| X | altezza dell'immagine risultante |
Tutte le distanze e le altezze specificate sono generalmente misurate in metri.
In fisica, il concetto di ingrandimento è anche associato alla formula della lente sottile. È definito come il rapporto tra le dimensioni dell'immagine e l'altezza dell'oggetto, cioè H / h. Può essere designato con la lettera G.
Devi sapere questo per ottenere la formulauna lente sottile che raccoglie o diffonde. Il disegno inizia con il fatto che entrambe le lenti hanno una propria rappresentazione schematica. Entrambi sembrano un segmento di linea. Solo per quello che raccoglie alle sue estremità le frecce sono dirette verso l'esterno, e per quello che disperde - verso l'interno di questo segmento.
Adesso a questo segmento è necessario disegnareperpendicolare al suo centro. Questo rappresenterà l'asse ottico principale. Su di esso, su entrambi i lati della lente alla stessa distanza, dovrebbe contrassegnare i punti focali.
L'oggetto che vuoi costruire viene disegnato sotto forma di una freccia. Ti mostra dove si trova la parte superiore dell'articolo. In generale, l'oggetto è posizionato parallelamente all'obiettivo.
Per costruire un'immagine di un oggetto,è sufficiente trovare i punti delle estremità dell'immagine e poi collegarli. Ciascuno di questi due punti può essere ottenuto dall'intersezione di due raggi. I più facili da costruire sono due di loro.
In esecuzione da un punto specificato parallelo al principaleasse ottico. Dopo aver contattato l'obiettivo, passa attraverso il fuoco principale. Se stiamo parlando di una lente di raccolta, allora questo fuoco si trova dietro la lente e il raggio lo attraversa. Quando si considera un raggio di diffusione, il raggio deve essere diretto in modo che la sua continuazione passi attraverso il fuoco davanti alla lente.
Passando direttamente attraverso il fuoco ottico dell'obiettivo. Non cambia direzione dopo di lei.
Ci sono situazioni in cui l'articolo viene consegnatoperpendicolare all'asse ottico principale e termina su di esso. Quindi è sufficiente costruire un'immagine di un punto che corrisponde al bordo di una freccia che non giace sull'asse. E poi disegna una perpendicolare da esso all'asse. Questa sarà l'immagine dell'oggetto.
L'intersezione dei punti tracciati fornisce un'immagine.Un'immagine reale si ottiene in una sottile lente convergente. Cioè, si ottiene direttamente all'intersezione dei raggi. Un'eccezione è la situazione in cui l'oggetto viene posizionato tra l'obiettivo e il fuoco (come in una lente d'ingrandimento), quindi l'immagine risulta essere immaginaria. Per lo scattering risulta sempre essere immaginario. Dopotutto, si ottiene all'intersezione non dei raggi stessi, ma delle loro estensioni.
È consuetudine disegnare l'immagine reale con una linea continua. Ma l'immaginario è punteggiato. Ciò è dovuto al fatto che il primo è effettivamente lì e il secondo si vede solo.
È conveniente farlo sulla base di un disegno che illustri la costruzione di un'immagine reale in una lente di raccolta. La designazione dei segmenti è indicata nel disegno.
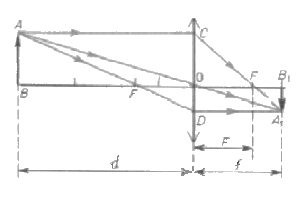
La sezione ottica è chiamata geometrica per un motivo. Avrai bisogno della conoscenza di questa particolare sezione della matematica. Per prima cosa devi considerare i triangoli AOB e A1OV1... Sono simili perché hanno due angoli uguali (dritto e verticale). Dalla loro somiglianza deriva che i moduli dei segmenti A1il1 e AB si riferiscono come moduli dei segmenti OB1 e OV.
Altri due triangoli risultano essere simili (basati sullo stesso principio in due angoli): COF e A1FB1... In essi, i rapporti di tali moduli di segmenti sono uguali: А1il1 con CO e FB1con DI. Sulla base della costruzione, i segmenti AB e CO saranno uguali. Pertanto, i lati di sinistra delle uguaglianze di relazione indicate sono gli stessi. Pertanto, anche il diritto è uguale. Cioè, OV1 / ОВ è uguale a FB1/ DI.
In questa uguaglianza, i segmenti indicati dai punti possono essere sostituiti dai corrispondenti concetti fisici. Quindi OV1 È la distanza dall'obiettivo all'immagine. RH è la distanza dall'oggetto all'obiettivo. DI - lunghezza focale. Un segmento FB1 è uguale alla differenza tra la distanza dall'immagine e il fuoco. Pertanto, può essere riscritto in un modo diverso:
f / d = (f - F) / F o Ff = df - dF.
Per ricavare la formula per una lente sottile, l'ultima uguaglianza deve essere divisa per dfF. Quindi si scopre:
1 / d + 1 / f = 1 / F.
Ha la formula di una sottile lente di raccolta.La lunghezza focale divergente è negativa. Ciò porta a un cambiamento nell'uguaglianza. È vero, è insignificante. È solo che nella formula di una lente a diffusione sottile c'è un segno meno prima del rapporto 1 /F. Cioè:
1 / d + 1 / f = - 1 / F.
Condizione. La lunghezza focale della lente di raccolta è di 0,26 m, è necessario calcolare il suo ingrandimento se l'oggetto si trova a una distanza di 30 cm.
Decisione. Dovrebbe iniziare con l'introduzione delle designazioni e la conversione delle unità in C. Quindi, noto d = 30 cm = 0,3 me F = 0,26 m Ora bisogna scegliere le formule, quella principale è quella indicata per l'ingrandimento, la seconda è per una lente collettrice sottile.
Devono essere combinati in qualche modo. Per fare ciò, dovrai considerare un disegno per costruire un'immagine in una lente di raccolta. Si può vedere da tali triangoli che Г = H / h= f / d. Cioè, per trovare l'ingrandimento, dovrai calcolare il rapporto tra la distanza dall'immagine e la distanza dall'oggetto.
Il secondo è noto. Ma si suppone che la distanza dall'immagine derivi dalla formula indicata in precedenza. Si scopre che
f = dF / (d - F).
Ora queste due formule devono essere combinate.
Г = dF / (d(d - F)) = F / (d - F).
In questo momento, la soluzione del problema per la formula per una lente sottile è ridotta a calcoli elementari. Resta da sostituire i valori noti:
G = 0,26 / (0,3 - 0,26) = 0,26 / 0,04 = 6,5.
Risposta: l'obiettivo fornisce un ingrandimento di 6,5 volte.

Condizione. La lampada si trova a un metro dalla lente di raccolta. L'immagine della sua spirale è ottenuta su uno schermo a 25 cm dall'obiettivo Calcola la lunghezza focale dell'obiettivo specificato.
Decisione. Dovrebbe scrivere i seguenti valori nei dati: d = 1 me f = 25 cm = 0,25 m Questa informazione è sufficiente per calcolare la lunghezza focale dalla formula per una lente sottile.
Quindi 1 /F = 1/1 + 1 / 0,25 = 1 + 4 = 5. Ma l'attività richiede di conoscere la messa a fuoco, non la potenza ottica. Pertanto, resta solo da dividere 1 per 5 e ottieni la lunghezza focale:
F = 1/5 = 0,2 m.
Risposta: la lunghezza focale della lente di raccolta è di 0,2 m.
condizione... La candela è stata posta a una distanza di 15 cm dalla lente di raccolta. La sua potenza ottica è di 10 diottrie. Lo schermo dietro l'obiettivo è posizionato in modo da ottenere un'immagine nitida della candela su di esso. A cosa è uguale questa distanza?
Decisione. Dovrebbe scrivere i seguenti dati in un breve record: d = 15 cm = 0,15 m, D = 10 diottrie. La formula mostrata sopra dovrebbe essere scritta con una leggera modifica. Vale a dire, sul lato destro dell'uguaglianza, metti D invece di 1 /F.
Dopo diverse trasformazioni, si ottiene la seguente formula per la distanza dall'obiettivo all'immagine:
f = d / (dD - uno).
Ora devi sostituire tutti i numeri e contare. Risulta un tale valore per f: 0,3 m.
Risposta: la distanza dall'obiettivo allo schermo è di 0,3 m.

Condizione. L'oggetto e la sua immagine sono separati l'uno dall'altro di 11 cm La lente di raccolta fornisce un ingrandimento di 3 volte. Trova la sua lunghezza focale.
Decisione. La distanza tra l'oggetto e la sua immagine è opportunamente indicata da una lettera L = 72 cm = 0,72 m. Ingrandimento G = 3.
Qui sono possibili due situazioni.Il primo è che il soggetto è dietro il fuoco, cioè l'immagine è reale. Nella seconda, c'è un oggetto tra il fuoco e l'obiettivo. Quindi l'immagine è dalla stessa parte dell'oggetto ed è immaginaria.
Consideriamo la prima situazione. L'oggetto e l'immagine si trovano sui lati opposti della lente di raccolta. Qui puoi scrivere la seguente formula: L = d + f. La seconda equazione dovrebbe essere scritta: Г = f / d. È necessario risolvere il sistema di queste equazioni con due incognite. Per fare ciò, sostituire L di 0,72 me G di 3.
Dalla seconda equazione risulta che f = 3d. Quindi il primo viene trasformato in questo modo: 0,72 = 4d. È facile contare da esso d = 0,18 (m). Ora è facile definirlo f = 0,54 (m).
Resta da usare la formula della lente sottile per calcolare la lunghezza focale. F = (0,18 * 0,54) / (0,18 + 0,54) = 0,135 (m). Questa è la risposta per il primo caso.
Nella seconda situazione, l'immagine è immaginaria e la formula per L sarà diverso: L = f - d. La seconda equazione per il sistema sarà la stessa. Discutendo in modo simile, lo troviamo d = 0,36 (m), e f = 1,08 (m). Un calcolo simile della lunghezza focale darà il seguente risultato: 0,54 (m).
Risposta: la lunghezza focale dell'obiettivo è 0,135 mo 0,54 m.
Il percorso dei raggi in una lente sottile è importanteapplicazione pratica dell'ottica geometrica. Dopotutto, vengono utilizzati in molti dispositivi, da semplici lenti di ingrandimento a microscopi e telescopi di precisione. Pertanto, è necessario conoscerli.
La formula derivata di una lente sottile consente di risolveremolti compiti. Inoltre, ti consente di trarre conclusioni su quale immagine danno i diversi tipi di lenti. In questo caso, è sufficiente conoscere la sua lunghezza focale e la distanza dall'oggetto.


























