
AC電源が接続されている場合抵抗に接続すると、タイミング図のどの時点でも回路内の電流と電圧は互いに比例します。これは、電流曲線と電圧曲線が同時にピークになることを意味します。そうすることで、電流と電圧が同相であると言います。
ここで、コンデンサが交流回路でどのように動作するかを考えてみましょう。

交流電圧が接続されている場合コンデンサーの両端の電圧の最大値は、回路を流れる電流の最大値に比例します。ただし、電圧正弦波のピークはピーク電流と同時に発生しません。
この例では、電流の瞬時値はその最大値は、電圧よりも 4 分の 1 周期 (90 エル度) 早い。この場合、「電流は電圧より90°進んでいる」と言います。
DC回路の状況と違い、ここでは V / I 値は一定ではありません。それにもかかわらず、V max / I max 比は非常に有用な量であり、電気工学ではコンポーネントの静電容量 (Xc) と呼ばれます。この値は依然として電圧と電流の比率を表しているため、物理的な意味では抵抗であり、その測定単位はオームです。コンデンサの Xc 値は、その静電容量 (C) と交流電流の周波数 (f) に依存します。
交流回路のコンデンサーなので実効値電圧が印加されると、同じ交流電流がこの回路に流れますが、これはコンデンサによって制限されます。この制限は、コンデンサのリアクタンスによるものです。

したがって、コンデンサ以外のコンポーネントを含まない回路の電流値は、オームの法則の別のバージョンによって決定されます
そしてRMS = URMS / バツC
どこ URMS - 二乗平均平方根 (実効) 電圧値。 Xと DC バージョンのオームの法則の R の値を置き換えます。
これで、回路内のコンデンサが交流電流は、定抵抗器とはまったく異なる動作をするため、ここでの状況はより複雑になります。このような連鎖で発生するプロセスをよりよく理解するために、そのような概念をベクトルとして導入すると便利です。
ベクトルの主なアイデアは\ u200b \ u200bのアイデアです時変信号の複素数は、複素数 (時間に依存しない) と、時間の関数である複雑な信号の積として表すことができます。
たとえば、関数 A cos (2πνt + θ) を単純に複素定数 A ∙ e として表すことができます。jΘ .
ベクトルは大きさ (またはモジュラス) と角度で表されるため、XY 平面内で回転する矢印 (またはベクトル) によってグラフィカルに表されます。
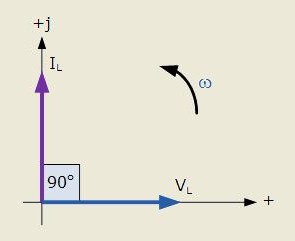
コンデンサの両端の電圧が電流に関して「遅れ」、それらを表すベクトルは、上の図に示すように、複素平面に配置されます。この図では、電流と電圧のベクトルは時計回りの動きとは逆方向に回転します。
この例では、コンデンサの電流は次によるものです。その定期的な充電。交流回路のコンデンサは周期的に電荷を蓄積および放電する能力を持っているため、コンデンサと電源との間で一定のエネルギー交換が行われます。これは、電気工学では無効エネルギーと呼ばれます。
