
19世紀初頭のベルリンの幾何学者ヤコブシュタイナー3つの村をどのように接続するかというタスクを設定して、それらの長さが最短になるようにします。その後、彼はこの問題を一般化しました。平面上の点を見つけて、それから他のn個の点までの距離が最小になるようにする必要があります。 20世紀には、このトピックに関する作業が続けられました。いくつかのポイントを取り、それらの間の距離が最短になるようにそれらを接続することが決定されました。これはすべて、調査中の問題の特殊なケースです。
クラスカルのアルゴリズムは「欲張り」アルゴリズムに属します(グラデーションとも呼ばれます)。その本質は、あらゆる段階で最大の利益です。欲張りアルゴリズムは、必ずしも問題の最善の解決策を提供するとは限りません。特定の問題に適用すると、それらが最適な解決策を提供することを示す理論があります。これがマトロイドの理論です。クラスカルのアルゴリズムはそのような問題に属します。
考慮されたアルゴリズムは、最適なものを構築しますワイヤーフレームグラフ。それに関する問題は次のとおりです。複数のエッジとループのない無向グラフが与えられ、そのエッジのセットに重み関数wが与えられます。これは、各エッジeに数値(エッジの重み)w(e)を割り当てます。エッジのセットからの各サブセットの重みは、そのエッジの重みの合計によって決定されます。最小の重量のフレームを見つける必要があります。
クラスカルのアルゴリズムはこのように機能します。まず、元のグラフのすべてのエッジが重みの昇順で配置されます。最初、ワイヤーフレームにはエッジが含まれていませんが、グラフのすべての頂点が含まれています。アルゴリズムの次のステップの後、スケルトンのすでに構築された部分であるスパニングフォレストに1つのエッジが追加されます。恣意的に選ばれるわけではありません。ワイヤーフレームに属さないグラフのすべてのエッジは、赤と緑と呼ぶことができます。各赤いエッジの頂点は、建設中のフォレストの同じ接続コンポーネントにあり、緑のエッジの頂点は異なるものにあります。したがって、そこに赤いエッジを追加するとサイクルが表示され、緑の場合、このステップの後に取得されるフォレスト内の接続性コンポーネントは1つ少なくなります。したがって、結果の構造に赤いエッジを追加することはできませんが、緑のエッジを追加してフォレストを作成することはできます。そして、最小限の重量で緑のエッジが追加されます。その結果、最も軽いフレームになります。
現在のフォレストFを示しましょう。グラフの頂点のセットを接続領域に分割します(それらの和集合はFを形成し、ペアで交差しません)。赤いエッジには、同じ部分に両方の頂点があります。パーツ(x)は、頂点xごとに、xが属するパーツの名前を返す関数です。 Unite(x、y)は、x部分とy部分、および他のすべての部分の結合で構成される、新しいパーティションを構築する手順です。グラフのエッジの数をnとします。これらの概念はすべて、クラスカルのアルゴリズムに含まれています。実装:
グラフのすべてのエッジを1番目からn番目まで重みの昇順で配置します。 (ai、biは、番号iのエッジの頂点です)。
i = 1からnの場合。
x:=パート(ai)。
y:=パート(bi)。
xがyと等しくない場合は、(x、y)を結合し、エッジiをFに含めます。
Tをクラスカルのアルゴリズムを使用して作成された元のグラフのスケルトンとし、Sをその任意のスケルトンとします。 w(T)がw(S)を超えないことを証明する必要があります。
MをエッジのセットS、Pをエッジのセットとします。T. SがTと等しくない場合、Sに属さないフレームTのエッジetがあります。etをSにアタッチします。サイクルが形成されます。それをCと呼びましょう。Cから任意のエッジesを削除します。 Sに属します。エッジがあり、その中にピークがいくつもあるため、新しいフレームを取得します。クラスカルのアルゴリズムにより、w(et)は最大でw(es)であるため、その重みはw(S)を超えません。 Tが得られるまで、この操作を繰り返します(エッジSをエッジTに置き換えます)。後続の各フレームの重みは前のフレームの重みより大きくないため、w(T)は大きくなりません。 w(S)。
また、クラスカルのアルゴリズムの正しさは、マトロイドに関するラドー-エドモンズの定理に基づいています。
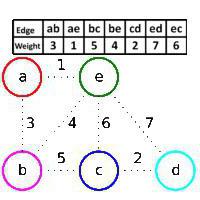
頂点a、b、c、d、eとエッジ(a、b)、(a、e)、(b、c)、(b、e)、(c、d)、(c、e)、(d、e)。リブの重量を表と図に示します。最初に、構築中のフォレストFにはグラフのすべての頂点が含まれ、エッジは含まれていません。クラスカルのアルゴリズムは、最初にエッジ(a、e)を追加します。これは、エッジ(a、e)の重みが最小であり、頂点aとeがフォレストFの異なる連結成分にあるため(エッジ(a、e)は緑色)、次にエッジを追加します。 (c、d)したがって、このエッジはFに属さないグラフのエッジの中で最小の重みを持ち、緑色であるため、同じ理由でエッジ(a、b)が追加されます。ただし、エッジ(b、e)は、残りのエッジの重みが最小であっても、赤であるためスキップされます。頂点bとeは、フォレストFの同じ連結成分に属します。つまり、追加すると、エッジ(b、e)からFまで、サイクルを形成します。次に、緑のエッジ(b、c)が追加され、赤のエッジ(c、e)がスキップされてから、d、eが追加されます。したがって、エッジ(a、e)、(c、d)、(a、b)、(b、c)が順番に追加されます。初期グラフの最適なスケルトンはそれらで構成されています。この場合、アルゴリズムは次のように機能します 描きました。例はこれを示しています。

この図は、2つの連結成分で構成されるグラフを示しています。太線は、クラスカルアルゴリズムを使用して構築された最適なワイヤーフレーム(緑)のエッジを示しています。

上の図は元のグラフを示し、下の図は考慮されたアルゴリズムを使用して構築された最小重みフレームワークを示しています。
追加されたエッジのシーケンス:(1,6); (0.3)、(2.6)または(2.6)、(0.3)-関係ありません。 (3.4); (0.1)、(1.6)または(1.6)、(0.1)も無関心です(5.6)。

クラスカルのアルゴリズムは、たとえば、通信の敷設、各国の集落の新しい近隣の道路、およびその他の場合に最適化するための実用的なアプリケーションを見つけます。
