
В начале 19 века геометр из Берлина Якоб Штейнер nustatyti užduotį, kaip prijungti tris kaimus, kad jų ilgis būtų trumpiausias. Vėliau jis apibendrino šią problemą: reikia rasti tašką plokštumoje, kad atstumas nuo jo iki kitų taškų būtų mažiausias. XX amžiuje ši tema tęsėsi. Buvo nuspręsta imtis kelių punktų ir sujungti juos taip, kad atstumas tarp jų būtų trumpiausias. Visa tai yra ypatingas nagrinėjamos problemos atvejis.
Алгоритм Краскала относится к "жадным" алгоритмам (jie taip pat vadinami gradientu). Jų esmė - didžiausias pelnas kiekviename žingsnyje. Ne visada „gobšus“ algoritmai suteikia geriausią problemos sprendimą. Yra teorija, kuri rodo, kad, pritaikius konkrečias užduotis, jie suteikia optimalų sprendimą. Tai yra matroidų teorija. Kraskalio algoritmas nurodo tokias problemas.
Aptariamas algoritmas sukurtas optimaliaikadro grafikas. Problema yra tokia. Pateikiamas netiesioginis grafikas be kelių kraštų ir kilpų, o jo kraštų rinkinyje nurodoma svorio funkcija w, kuri kiekvienam kraštui e suteikia skaičių - krašto svoris - w (e). Kiekvieno pogrupio svoris nuo briaunų rinkinio nustatomas pagal jo kraštų svorį. Reikia rasti mažiausio svorio skeletą.
Kruskalio algoritmas veikia taip.Pirma, visi pradinio grafiko kraštai yra išdėstyti didėjančia svorio tvarka. Iš pradžių skeletas neturi jokių kraštų, tačiau apima visas grafiko viršūnes. Po kito algoritmo žingsnio vienas kraštas pridedamas prie jau sukonstruotos skeleto dalies, kuri yra besitęsiantis miškas. Jis nėra pasirinktas atsitiktinai. Visi grafiko kraštai, nepriklausantys laidiniam rėmui, gali būti vadinami raudona ir žalia. Kiekvieno raudono krašto viršūnės yra tame pačiame statomo miško jungties komponente, o žalio krašto viršūnės yra skirtingos. Todėl, jei jūs ten pridėsite raudoną kraštą, pasirodys ciklas, o jei jis yra žalias, miške sujungimo komponentas, gautas atlikus šį žingsnį, bus vienas mažiau. Taigi prie gautos konstrukcijos negalima pridėti jokio raudono krašto, tačiau norint gauti mišką, galima pridėti bet kokį žalią kraštą. Pridedamas žalias kraštas su minimaliu svoriu. Rezultatas yra lengviausias rėmas.
Pažymėkite dabartinį mišką F.Diagramos viršūnių rinkinys suskaidomas į susietus domenus (jų sąjungos formos F, ir jos nesiskiria poromis). Raudonuosiuose kraštuose abi viršūnės yra vienoje dalyje. Dalis (x) yra funkcija, kuri kiekvienai vertex x grąžina tos dalies, kuriai priklauso x, pavadinimą. Unite (x, y) yra procedūra, kuria sukuriamas naujas skaidinys, susidedantis iš x ir y dalių ir visų kitų dalių derinimo. Leiskite n būti grafiko kraštų skaičius. Visos šios sąvokos yra įtrauktos į „Kraskal“ algoritmą. Įgyvendinimas:
Rūšiuoti visus grafiko kraštus nuo 1 iki n. Didėjančia tvarka. (ai, bi yra krašto viršūnės su skaičiumi i).
i = 1 iki n.
x: = dalis (ai).
y: = dalis (bi).
Jei x nėra lygus y, tada Unite (x, y), įtraukite kraštą i F.
Tegu yra pirminio grafo, sukonstruoto naudojant Kruskalio algoritmą, griaučiai, o S - savavališkas griaučiai. Turime įrodyti, kad w (T) neviršija w (S).
Tegul M yra kraštų aibė S, P - kraštų aibėT. Jei S nėra lygus T, tada yra rėmelio T kraštas et, kuris nepriklauso S. Mes prijungiame etą prie S. Suformuojamas ciklas, pavadinkime jį C. Mes pašaliname iš C bet kokius S priklausančius kraštus. Mes gauname naują rėmą, nes kraštai, ir jame yra tiek pat viršukalnių. Jo svoris neviršija w (S), nes pagal Kruskalio algoritmą w (et) yra ne daugiau kaip w (es). Mes kartosime šią operaciją (pakeisdami kraštus S kraštais T), kol gausime T. Kiekvieno paskesnio gauto rėmo svoris nėra didesnis už ankstesnio svorį, iš kur išplaukia, kad w (T) nėra didesnis nei w (S).
Be to, Kruskalio algoritmo teisingumas išplaukia iš Rado-Edmondso teoremos apie matroidus.
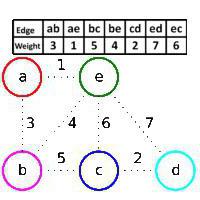
Grafikas su viršūnėmis a, b, c, d, e ir kraštais (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Šonkaulių svoriai parodyti lentelėje ir paveiksle. Iš pradžių statomame miške F yra visos grafiko viršūnės ir nėra jokių kraštų. Kruskalio algoritmas pirmiausia prideda kraštą (a, e), nes jo svoris mažiausias, o viršūnės a ir e yra skirtinguose miško F komponentuose (kraštas (a, e) yra žalias), tada kraštas (c, d), todėl kad šis kraštas turi mažiausiai F nepriklausančio grafiko kraštų svorio ir yra žalias, tada kraštas (a, b) pridedamas dėl tų pačių priežasčių. Bet kraštas (b, e) praleidžiamas, net jei jis turi mažiausią likusių kraštų svorį, nes jis yra raudonas: viršūnės b ir e priklauso tam pačiam sujungtam miško komponentui F, tai yra, jei prie F pridėsime kraštą (b, e), ciklas. Tada pridedamas žalias kraštas (b, c), praleidžiamas raudonas kraštas (c, e) ir tada d, e. Taigi, kraštai (a, e), (c, d), (a, b), (b, c) pridedami nuosekliai. Iš jų susideda optimalus pradinio grafo skeletas. Tokiu atveju algoritmas veikia tokiu atveju Tapyta. Tai parodė pavyzdys.

Paveiksle parodyta diagrama, susidedanti iš dviejų sujungtų komponentų. Ryškios linijos rodo optimalaus vielinio rėmo (žalios spalvos) kraštus, pastatytą naudojant „Kruskal“ algoritmą.

Viršutiniame paveiksle pavaizduotas pradinis grafikas, o apatiniame - minimalus svorio skeletas, pastatytas jam naudojant nagrinėjamą algoritmą.
Pridėtų kraštų seka: (1,6); (0,3), (2,6) arba (2,6), (0,3) - nesvarbu; (3.4); (0,1), (1,6) arba (1,6), (0,1) taip pat yra abejingas (5,6).

Kruskalio algoritmas yra praktiškai pritaikomas, pavyzdžiui, optimizuojant komunikacijų, kelių tiesimą kiekvienos šalies naujų gyvenviečių rajonuose, taip pat kitais atvejais.


























