Binariniai santykiai ir jų savybės

Platus santykių asortimentas rinkinių pavyzdžiukartu su daugybe sąvokų, pradedant jų apibrėžtimis ir baigiant analitine paradoksų analize. Straipsnyje aptariamos sąvokos įvairovė yra begalinė. Nors kalbant apie dvejopus tipus, tai reiškia dvejetainius santykius tarp kelių kiekių. Ir taip pat tarp objektų ar pareiškimų.

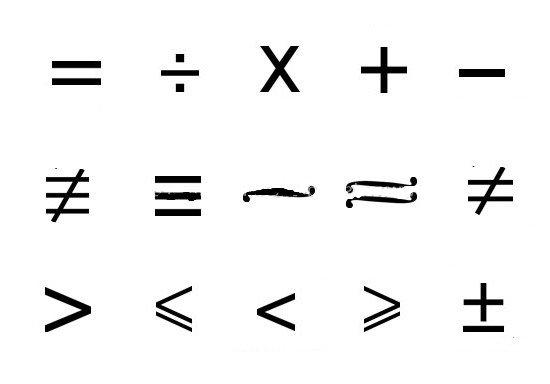
Paprastai skiriami dvejetainiai santykiaisimbolis R, tai yra, jei xRx bet kuriai x reikšmei iš lauko R, ši savybė vadinama refleksine, kurioje x ir x yra priimtini minties objektai, o R tarnauja kaip ženklas apie vieną ar kitą asmenų tarpusavio sujungimo formą. Tuo pačiu metu, jei išreiškiamas xRy® arba yRx, tai reiškia simetrijos būseną, kur ® yra implicijos ženklas, panašus į „jei ..., tada ...“ aljansą, ir galiausiai teksto iššifravimas ®xRz pasakys apie tranzitinį sujungimą, o знак ženklas yra jungtis.

Dvejetainis ryšys, kuris vyksta vienu meturefleksyvus, simetriškas ir tranzitinis, vadinamas lygiavertiškumo santykiu. Santykis f yra funkcija, o iš Î f ir Î f seka lygybę y = z. Paprasta dvejetainė funkcija gali būti lengvai pritaikyta dviem paprastiems argumentams, išdėstytiems tam tikroje eilėje, ir tik šiuo atveju tai suteikia vertę, nukreiptą į šias dvi išraiškas, paimtas konkrečiu atveju.

Turėtų būti pasakyta, kad f žemėlapiai x – y,

Remiantis tuo, kas išdėstyta, dvejetainių santykių lygiavertiškumo santykį lemia savybės:

• refleksyvumas - santykis (M ~ N);
• simetrija - jei lygybė yra M ~ N, tai bus N ~ M;
• tranzitumas - jei du lygiai M ~ N ir N ~ P, tada kaip rezultatas M ~ P.

Apsvarstykite nurodytas dvejetainių santykių savybesdaugiau informacijos. Refleksyvumas yra viena iš tam tikrų santykių charakteristikų, kur kiekvienas tiriamo rinkinio elementas yra šioje lygybėje. Pavyzdžiui, tarp a = c ir a ³ c yra refleksyvios jungtys, nes visada a = a, c = c, a ³ a, c ³ c. Tuo pačiu metu nelygybės santykis a> c yra antirefleksinis, nes nelygybės egzistavimas yra neįmanomas a> a. Šios savybės aksiomą koduoja ženklai: aRc® aRa Ù cRc, čia simbolis ® reiškia, kad žodis „pritraukia“ (arba „reiškia“), o ženklas veikia kaip sąjunga „ir“ (arba kartu). Iš šio teiginio darytina išvada, kad aRc tiesos atveju aRa ir cRc taip pat yra teisingos.

Simetrija reiškia ryšįir tuo atveju, jei mąstymo objektai yra keičiami, ty su simetrišku ryšiu, objektų pertvarkymas nesukelia „dvejetainių santykių“ tipo transformacijos. Pavyzdžiui, lygybės santykis a = c yra simetriškas dėl santykio c = a lygiavertiškumo; A¹c sprendimas taip pat yra tas pats, nes jis reaguoja į ryšį su a¹a.

Tranzitinis rinkinys yra toks turtaskai įvykdomas šis reikalavimas: y Î x, z Î y ® z Î x, kur ® veikia kaip ženklas, pakeičiantis žodžius: Formulė aiškinama žodžiu taip: "Jei y priklauso nuo x, z priklauso y, tada z taip pat priklauso nuo x".