
Datorzinātne kā kolekcijas metožu zinātne,dažādu datu pasūtīšana un apstrāde sāk attīstīties divdesmitā gadsimta vidū. Lai arī daži vēsturnieki uzskata, ka datorzinātņu veidošanās sākās 17. gadsimtā, izgudrojot pirmo mehānisko kalkulatoru, to visvairāk saista ar progresīvākas skaitļošanas laikmetu. 20. gadsimta 40. gados, parādoties pirmajiem datoriem, datorzinātne ieguva jaunu impulsu attīstībā.
Tas bija līdz ar pirmo datoru parādīšanosradās nepieciešamība izstrādāt jaunas lielu datu apjomu sistematizācijas, aprēķināšanas un apstrādes metodes, kā arī izstrādāt algoritmus, kas ļautu pilnībā izmantot jauno datoru potenciālu. Datorzinātne ieguva patstāvīgas zinātniskās disciplīnas statusu un no matemātisko aprēķinu plaknes pārcēlās uz skaitļošanas sistēmu kopumā.

Visa mūsdienu datorzinātne ir balstīta uzloģiskās operācijas. Tos var saukt par būtisku komponentu. Programmēšanas datorsistēmās loģiskas operācijas jēdziens ir noteikta darbība, pēc kuras tiek ģenerēta jauna koncepcija vai vērtība, kas tiek veidota, balstoties uz esošajām koncepcijām. Šādu darbību kopums var atšķirties atkarībā no procesora elementa, kuram jāizpilda komandas. Tomēr ir dažas operācijas, kas ir raksturīgas gandrīz visām esošajām sistēmām. Tās ir operācijas, kas darbojas ar pašu nozīmju saturu, piemēram, noliegumu, vai darbības, kas maina jēdziena kvantitatīvās īpašības - saskaitīšana, atņemšana, reizināšana, dalīšana.
Tā kā loģikas algebra ietver darbu pieabstraktas koncepcijas, tad vispārinātie datu tipi darbojas kā visu loģisko operāciju operandi. Klasiskie elementi, ar kuriem darbojas ierosināšanas algebra, ir apgalvojumi, nepatiesi vai patiesi. Elektronikā un programmēšanā šo terminu aprakstīšanai tiek izmantoti Būla mainīgie lielumi true un false vai veseli skaitļi vērtības 1 (true) un 0 (false). Šo vērtību kombinācija, lai arī cik neticami tā izklausītos, ir saistīta ar vissarežģītāko un liela mēroga sistēmu darbu. Viss programmas kods, kas darbojas datorā vai jebkurā digitālā ierīcē, tiek dinamiski tulkots secībā un nullēs - universālā kodā, kuru var apstrādāt jebkurš procesors.
Kā minēts iepriekš, klasiskajāBūla algebra, ir 2 veidu funkcijas. Bināro datu tipu loģiskās pamatdarbības ir darbības, kas ietekmē pašu paziņojumu (vienota vai vienota operācija). Tas ietver arī operācijas, kas ģenerē jaunus paziņojumus, pamatojoties uz esošajām vērtībām (bināras vai dubultas operācijas). Loģisko operāciju secība ir tāda pati kā, veicot jebkurus matemātiskos aprēķinus: no kreisās uz labo, ņemot vērā iekavas.

Vienkāršākais un viens no slavenākajiemBūla loģikas funkcijas ir nolieguma funkcija. Šī vienkāršākā loģiskā darbība ir pretēja ievades operandam. Elektronikā šo darbību dažreiz sauc par inversiju. Piemēram, ja jūs apvēršat apgalvojumu “patiesība”, tad rezultāts būs “nepatiess”. Un otrādi - “nepatiesa” nozīmes noliegšana novedīs pie “patiesības” nozīmes. Šādu loģisku programmēšanas darbību ļoti bieži izmanto algoritmu sazarošanai un nākamās komandu kopas “izvēles” ieviešanai, pamatojoties uz esošajiem rezultātiem vai mainītajiem apstākļiem.
Programmēšanā un datorzinātnēs tiek izmantotaierobežots bināro (bināro) operāciju komplekts. Viņi savu vārdu ieguva no latīņu vārda bi, kas nozīmē "divi", un ir funkciju tips, kas ievada divus argumentus un rezultātā iegūst vienu jaunu vērtību. Patiesības tabulas tiek izmantotas, lai aprakstītu visas Būla algebras funkcijas.
Šī sistēma ir paredzēta konkrētamieejas operandu skaitu un apraksta visas iegūtās vērtības, kuras dotā loģiskā darbība var atgriezt ar noteiktu ievades parametru kopu.
Datorzinātnē un datortehnoloģijā visbiežāk izmantotās funkcijas ir loģiskās saskaitīšanas (disjunkcijas) un loģiskās reizināšanas (konjunktūras) operācijas.
Loģiskā darbība "UN" ir izvēles funkcijamazākais no diviem vai n ieejas operandiem. Ieejā šai funkcijai var būt divas (binārā funkcija), trīs vērtības (trīskārša) vai neierobežots skaits operandu (n-veida operācija). Aprēķinot funkcijas rezultātu, tas būs mazākais no sniegtajām ieejas vērtībām.
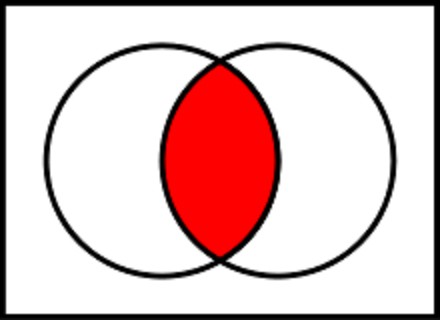
Analogs parastajā algebrā ir funkcijapavairošana. Tāpēc savienojuma darbību bieži sauc par loģisko reizināšanu. Rakstot funkciju, zīme ir vai nu reizināšanas zīme (punkts), vai ampersants. Apkopojot šīs funkcijas patiesības tabulu, jūs redzēsiet, ka funkcija iegūst vērtību "true" vai 1 tikai tad, ja visi ievades operandi ir patiesi. Ja vismaz viens no ievades parametriem ir vienāds ar nulli vai vērtību "false", tad funkcijas rezultāts būs arī "false".

Tas atspoguļo līdzību ar aritmētisko reizināšanu:reizinot jebkuru skaitli un skaitļu kopu ar 0, vienmēr tiks atgriezta 0. Šī loģiskā darbība ir komutatīva: secība, kādā tā saņem ievades parametrus, neietekmēs aprēķina galīgo rezultātu.
Vēl viena šīs funkcijas īpašība irasociativitāte vai kombinācija. Šis rekvizīts ļauj ignorēt aprēķinu kārtību, aprēķinot bināro darbību secību. Tāpēc 3 vai vairākām secīgām loģiskās reizināšanas operācijām nav jāņem vērā iekavas. Programmējot šo funkciju bieži izmanto, lai pārliecinātos, ka konkrētas komandas tiek izpildītas tikai tad, ja ir izpildīti noteikti nosacījumi.
Loģiskā darbība "OR" - sava veida Būla funkcija,kas ir analogs algebriskai pievienošanai. Citi šīs funkcijas nosaukumi ir loģisks papildinājums, disjunkcija. Tieši tāpat kā loģiskā reizināšanas operācija, disjunkcija var būt binārā (aprēķināt vērtību, pamatojoties uz diviem argumentiem), trīskārša vai n-ārija.

Patiesības tabula noteiktai loģiskai operācijaiir sava veida alternatīva konjunkcijai. Loģiskā OR operācija aprēķina maksimālo rezultātu starp piegādātajiem argumentiem. Disjunkcija izejā ņem vērtību "false" vai 0 tikai tad, ja visiem ievades parametriem ir vērtība 0 ("false"). Jebkurā citā gadījumā izeja būs "true" vai 1. Lai rakstītu šo funkciju, visbiežāk tiek izmantota pievienošanas matemātiskā zīme ("plus") vai divas vertikālas svītras. Otrā opcija ir izplatīta lielākajā daļā programmēšanas valodu un ir vēlama, jo tā ļauj skaidri nodalīt loģisko darbību no aritmētiskās.
Pamata loģiskās operācijas, neatkarīgi no tā, vai tās ir vienotas,binārā, trīskāršā vai citas funkcijas ir pakļautas noteiktiem noteikumiem un īpašībām, kas raksturo viņu uzvedību. Viena no šādām pamatīpašībām, kas piemīt iepriekš aprakstītajām loģiskajām funkcijām, ir komutativitāte.

Šis rekvizīts nodrošina permutācijuoperandu vietās funkcijas vērtība nemainīsies. Ne visām operācijām ir šis īpašums. Atšķirībā no konjunkcijas un disjunkcijas, kas atbilst komutativitātes prasībām, matricas reizināšanas funkcija nav tāda, un, pārkārtojot faktorus šajā operācijā, mainīsies rezultāts, kā arī eksponācija.
Vēl viens svarīgs īpašums, ko bieži izmanto elektronikā un shēmās, ir loģisko darbību pāru pakļautība de Morgan likumiem.

Šie likumi savieno loģisko darbību pārus arizmantojot loģiskās noliegšanas funkciju, tas ir, tie ļauj izteikt vienu loģisku darbību, izmantojot citu. Piemēram, savienojuma noliegšanas funkciju var izteikt, izmantojot atsevišķu operandu negatīvo disjunkciju. Ar šo likumu palīdzību loģiskās darbības "AND", "OR" var savstarpēji izteikt un ieviest ar minimālām aparatūras izmaksām. Šis īpašums ir ārkārtīgi noderīgs ķēdēs, jo tas ietaupa resursus, aprēķinot un veidojot mikroshēmas.


























