Relacje binarne i ich właściwości

Широкий спектр отношений на примере множеств Towarzyszy temu duża liczba pojęć, zaczynając od ich definicji, a kończąc na analitycznej analizie paradoksów. Różnorodność pojęć omówionych w artykule na temat zestawu jest nieskończona. Chociaż mówiąc o typach podwójnych, oznacza to relacje binarne między kilkoma wielkościami. A także między przedmiotami lub wypowiedziami.

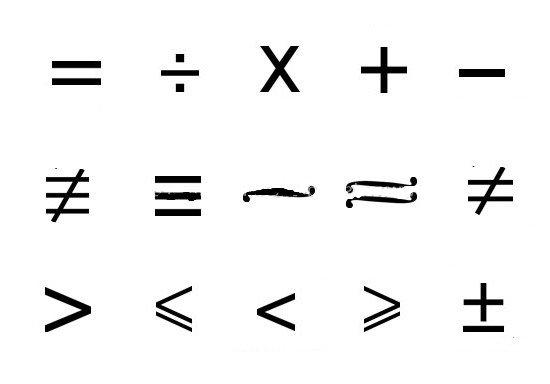
Z reguły relacje binarne są oznaczone przezsymbol R, to znaczy, jeśli xRx dla dowolnej wartości x z pola R, taka właściwość jest nazywana odblaskową, w której x i x są akceptowanymi przedmiotami myśli, a R służy jako znak jakiejś formy relacji między jednostkami. Jednocześnie, jeśli wyrażamy xRy® lub yRx, oznacza to stan symetrii, gdzie ® jest znakiem implikacyjnym, podobnym do unii „jeśli ... to ...”. I wreszcie dekodowanie napisu (xRy Ùy Rz) ®xRz mówi o związku przechodnim, a znak jest spójnikiem.

Relacja binarna, która dzieje się jednocześniezwrotny, symetryczny i przechodni, nazywany jest relacją równoważności. Zależność f jest funkcją, a równość y = z wynika z Î f i Î f. Prostą funkcję binarną można łatwo zastosować do dwóch prostych argumentów ułożonych w określonej kolejności i tylko w tym przypadku zapewnia ona wartość skierowaną do tych dwóch wyrażeń wziętych w konkretnym przypadku.

Należy powiedzieć, że f odwzorowuje x na y,

jeśli f służy jako funkcja ze strefą wykrywania x istrefa wartości y. Jeśli jednak f ekstrapoluje x na y, i y Í z, oznacza to, że f pokazuje x w z. Prosty przykład: jeśli f (x) = 2x jest poprawne dla dowolnej liczby całkowitej x, to mówią, że f odwzorowuje podpisany zestaw wszystkich znanych liczb całkowitych na zbiór tych samych liczb całkowitych, ale tym razem liczby parzyste. Jak wspomniano powyżej, relacje binarne, które są jednocześnie refleksyjne, symetryczne i przechodnie, są wzajemnymi relacjami równoważności.

Na podstawie powyższego związek równoważności relacji binarnych jest określony przez właściwości:

• współczynnik zwrotności (M ~ N);
• symetria - jeśli równość wynosi M ~ N, to będzie N ~ M;
• przechodniość - jeśli dwie równości M ~ N i N ~ P, to w rezultacie M ~ P.

Rozważ deklarowane właściwości relacji binarnychbardziej szczegółowo. Refleksyjność jest jedną z cech charakterystycznych niektórych połączeń, w których każdy element badanego zbioru jest w określonej równości ze sobą. Na przykład między liczbami a = c i a³ c są powiązania zwrotne, ponieważ zawsze a = a, c = c, a³ a, c³ c. Jednocześnie relacja nierówności a> c jest antyrefleksyjna ze względu na niemożność zaistnienia nierówności a> a. Aksjomat tej własności jest zakodowany za pomocą znaków: aRc® aRa Ù cRc, tutaj symbol ® oznacza słowo „pociąga za sobą” (lub „implikuje”), a znak Ù - działa jako związek „i” (lub koniunkcja). Z tego stwierdzenia wynika, że ​​jeśli orzeczenie aRc jest prawdziwe, wyrażenia aRa i cRc są również prawdziwe.

Symetria pociąga za sobą związekaw przypadku zamiany obiektów mentalnych, to znaczy w przypadku relacji symetrycznej, permutacja obiektów nie prowadzi do przekształcenia postaci „relacji binarnych”. Na przykład relacja równości a = c jest symetryczna ze względu na równoważność relacji c = a; wyrok a¹c jest również taki sam, ponieważ odpowiada powiązaniu z¹a.

Taką właściwością jest zbiór przechodnigdzie spełniony jest warunek: y Î x, z Î y ® z Î x, gdzie ® jest znakiem zastępującym słowa: „jeśli…, to…”. Formułę odczytuje się werbalnie w następujący sposób: „Jeśli y zależy od x, z należy do y, to z zależy również od x”.