
Trapez to szczególny przypadek czworokąta, yktórej jedna para boków jest równoległa. Termin „trapez” pochodzi od greckiego słowa τράπεζα, oznaczającego „stół”, „stół”. W tym artykule przyjrzymy się rodzajom trapezu i jego właściwościom. Ponadto dowiemy się, jak obliczyć poszczególne elementy tej figury geometrycznej. Na przykład przekątna trapezu równoramiennego, linia środkowa, obszar itp. Materiał jest prezentowany w stylu elementarnej popularnej geometrii, czyli w łatwo dostępnej formie.
Najpierw zastanówmy się, co to jestczworobok. Ten kształt jest szczególnym przypadkiem wielokąta o czterech bokach i czterech wierzchołkach. Dwa wierzchołki czworokąta, które nie sąsiadują ze sobą, nazywane są przeciwległymi. To samo można powiedzieć o dwóch niesąsiadujących ze sobą bokach. Główne typy czworokątów to równoległobok, prostokąt, romb, kwadrat, trapez i deltoid.

Wróćmy więc do trapezów.Jak powiedzieliśmy, ta figura ma dwie równoległe strony. Nazywane są bazami. Pozostałe dwie (nierównoległe) to boki. W materiałach egzaminów i różnych testów bardzo często można znaleźć zadania związane z trapezami, których rozwiązanie często wymaga od ucznia wiedzy, której program nie przewiduje. Szkolny kurs geometrii wprowadza studentów we właściwości kątów i przekątnych oraz linii środkowej trapezu równoramiennego. Ale oprócz tego wspomniana figura geometryczna ma inne cechy. Ale o nich trochę później ...
Istnieje wiele rodzajów tej figury. Najczęściej jednak zwyczajowo rozważa się dwa z nich - równoramienne i prostokątne.
1. Trapez prostokątny to figura, w której jeden z boków jest prostopadły do podstaw. Jego dwa kąty są zawsze równe dziewięćdziesięciu stopniom.
2. Trapez równoramienny to figura geometryczna o równych bokach. Oznacza to, że kąty u podstaw są również równe parami.

Główną zasadą jest użycietak zwane podejście zadaniowe. W zasadzie nie ma potrzeby wprowadzania nowych własności tej figury do teoretycznego toku geometrii. Można je otwierać i formułować w procesie rozwiązywania różnych problemów (lepszych niż systemowe). Jednocześnie bardzo ważne jest, aby nauczyciel wiedział, jakie zadania należy powierzyć uczniom w tym czy innym momencie procesu edukacyjnego. Co więcej, każda właściwość trapezu może być reprezentowana jako zadanie kluczowe w systemie zadaniowym.
Druga zasada to tzwspiralna organizacja badania „niezwykłych” właściwości trapezu. Oznacza to powrót w procesie uczenia się do indywidualnych cech danej figury geometrycznej. Ułatwia to uczącym się ich zapamiętywanie. Na przykład właściwość czterech punktów. Można to udowodnić zarówno poprzez badanie podobieństwa, jak i następnie za pomocą wektorów. A jednakowy rozmiar trójkątów sąsiadujących z bokami figury można udowodnić, stosując nie tylko właściwości trójkątów o równych wysokościach narysowanych na bokach leżących na jednej linii prostej, ale także za pomocą wzoru S = 1/2 (ab * sinα). Ponadto można opracować twierdzenie o sinusach na wpisanym trapezie lub trójkącie prostokątnym na opisanym trapezie itp.
Zastosowanie funkcji „poza programem”figura geometryczna w treści kursu szkolnego jest technologią zadaniową do ich nauczania. Stałe odwoływanie się do badanych właściwości przy przekazywaniu innych tematów pozwala studentom na głębsze zrozumienie trapezu i zapewnia sukces w rozwiązywaniu przydzielonych zadań. Przejdźmy więc do studiowania tej wspaniałej postaci.

Jak już zauważyliśmy, ta geometrycznaliczby po bokach są równe. Jest również znany jako regularny trapez. I dlaczego jest tak niezwykły i dlaczego otrzymał taką nazwę? Osobliwością tej figury jest to, że ma równe nie tylko boki i kąty u podstawy, ale także przekątne. Ponadto suma kątów trapezu równoramiennego wynosi 360 stopni. Ale to nie wszystko! Ze wszystkich znanych trapezów tylko wokół równoramiennego można opisać okrąg. Wynika to z faktu, że suma przeciwnych kątów tej figury wynosi 180 stopni i tylko pod tym warunkiem można opisać okrąg wokół czworokąta. Następną właściwością rozważanej figury geometrycznej jest to, że odległość od góry podstawy do rzutu przeciwległego wierzchołka na linię prostą zawierającą tę podstawę będzie równa linii środkowej.
Teraz zastanówmy się, jak znaleźć kąty trapezu równoramiennego. Rozważ rozwiązanie tego problemu, pod warunkiem, że znane są wymiary boków figury.
Zwykle oznacza się czworokątlitery A, B, C, D, gdzie BS i PIEKŁO są podstawami. W trapezie równoramiennym boki są równe. Przyjmiemy, że ich rozmiar jest równy X, a rozmiary podstaw są równe Y i Z (odpowiednio mniejsze i większe). Aby przeprowadzić obliczenia, należy narysować wysokość N. od kąta B. W wyniku otrzymujemy trójkąt prostokątny ABN, gdzie AB to przeciwprostokątna, a BN i AH to nogi. Obliczamy rozmiar nogi AH: od większej podstawy odejmujemy mniejszą, a wynik dzielimy przez 2. Piszemy to w postaci wzoru: (ZY)/2 = F. Teraz obliczamy kąt ostry trójkąta, używamy funkcji cos. Otrzymujemy następujący rekord: cos (β) = X / F. Teraz obliczamy kąt: β = arcos (X / F). Ponadto, znając jeden kąt, możemy określić drugi, w tym celu wykonujemy elementarną operację arytmetyczną: 180 - β. Wszystkie kąty są zdefiniowane.
Istnieje również drugie rozwiązanie tego problemu.Na początek obniżamy wysokość N. od narożnika Obliczamy wartość nogi BN. Wiemy, że kwadrat przeciwprostokątnej trójkąta prostokątnego jest równy sumie kwadratów nóg. Otrzymujemy: BN = √ (X2-F2). Następnie korzystamy z funkcji trygonometrycznej tg. W rezultacie mamy: β = arctan (BN / F). Znaleziono ostry róg. Następnie definiujemy kąt rozwarty w taki sam sposób, jak w pierwszej metodzie.
Najpierw zapiszmy cztery zasady. Jeśli przekątne w trapezie równoramiennym są prostopadłe, to:
- wysokość figury będzie równa sumie podstaw podzielonej przez dwa;
- jego wysokość i linia środkowa są równe;
- powierzchnia trapezu będzie równa kwadratowi wysokości (linia środkowa, połowa sumy podstaw);
- kwadrat przekątnej jest równy połowie kwadratu sumy podstaw lub dwukrotności kwadratu linii środkowej (wysokości).
Rozważmy teraz wzory określające przekątną trapezu równoramiennego. Ten blok informacji można z grubsza podzielić na cztery części:
1. Wzór na długość przekątnej z uwzględnieniem jej boków.
Zakładamy, że A to podstawa dolna, B to góra, C to równe boki, D to przekątna. W takim przypadku długość można określić w następujący sposób:
D = (C2 + A * B).
2. Wzory na długość przekątnej przez twierdzenie cosinusowe.
Przyjmujemy, że A to dolna podstawa, B to górna,C - równe boki, D - przekątne, α (u podstawy dolnej) i β (u podstawy górnej) - kąty trapezowe. Otrzymujemy następujące wzory, które można wykorzystać do obliczenia długości przekątnej:
- D = √ (A2 + C2-2A * C * cosα);
- D = √ (A2 + C2-2A * C * cosβ);
- D = √ (B2 + C2-2B * C * cosβ);
- D = √ (B2 + C2-2B * C * cosα).
3. Wzory na długość przekątnych trapezu równoramiennego.
Zakładamy, że A to podstawa dolna, B to góra, D to przekątna, M to linia środkowa, H to wysokość, P to powierzchnia trapezu, α i β to kąty między przekątnymi. Długość określamy według wzorów:
- D = (M2 + H2);
- D = √ (H2 + (A + B) 2/4);
- D = (H (A + B) / sinα) = √ (2P / sinα) = √ (2M * H / sinα).
W tym przypadku równość jest prawdziwa: sinα = sinβ.
4. Wzory na długość przekątnej pod względem boków i wysokości.
Zakładamy, że A to podstawa dolna, B to góra, C to boki, D to przekątna, H to wysokość, α to kąt przy podstawie dolnej.
Długość określamy według wzorów:
- D = √ (H2 + (A-P * ctgα) 2);
- D = √ (H2 + (B + P * ctgα) 2);
- D = (A2 + C2-2A * (C2-H2)).

Przyjrzyjmy się, co jest interesujące w tej figurze geometrycznej. Jak powiedzieliśmy, prostokątny trapez ma dwa kąty proste.
Oprócz klasycznej definicji istnieją równieżinny. Na przykład trapez prostokątny to trapez, którego jedna strona jest prostopadła do jego podstaw. Albo postać z kątami prostymi z boku. W tym typie trapezu wysokość jest równa bocznej stronie, która jest prostopadła do podstaw. Linia środkowa to odcinek linii, który łączy punkty środkowe dwóch boków. Właściwość wspomnianego elementu polega na tym, że jest on równoległy do baz i jest równy połowie ich sumy.
Przyjrzyjmy się teraz podstawowym wzorom,zdefiniowanie tej figury geometrycznej. W tym celu zakładamy, że A i B są fundamentami; C (prostopadle do podstaw) i D - boki prostokątnego trapezu, M - linia środkowa, α - kąt ostry, P - powierzchnia.
1.Bok, prostopadły do podstaw, jest równy wysokości figury (C = H) i jest równy iloczynowi długości drugiego boku D i sinusa kąta α o większej podstawie ( C = D * sina). Ponadto jest równy iloczynowi stycznej kąta ostrego α i różnicy podstaw: C = (A-B) * tgα.
2. Boczny bok D (nie prostopadły do podstaw) jest równy ilorazowi różnicy między A i B i cosinusem (α) kąta ostrego lub ilorazu wysokości figury H i sinusa kąt ostry: D = (AB) / cos α = C / sinα.
3. Bok, który jest prostopadły do podstaw, jest równy pierwiastkowi kwadratowemu z różnicy między kwadratem D - drugim bokiem - a kwadratem różnicy między podstawami:
C = (D2- (A-B) 2).
4. Bok D trapezu prostokątnego jest równy pierwiastkowi kwadratowemu z sumy kwadratu boku C i kwadratu różnicy między podstawami figury geometrycznej: D = √ (C2 + (A-B) 2).
5. Bok C jest równy ilorazowi dzielenia podwójnej powierzchni przez sumę jej podstaw: C = P / M = 2P / (A + B).
6. Powierzchnia jest określona przez iloczyn M (środkowa linia prostokątnego trapezu) przez wysokość lub bok prostopadły do podstaw: P = M * H = M * C.
7. Bok C jest równy ilorazowi dzielenia podwojonej powierzchni figury przez iloczyn sinusa kąta ostrego i sumy jego podstaw: C = P / M * sinα = 2P / ((A + B) * sina).
8. Wzory na boczną stronę prostokątnego trapezu przez jego przekątne i kąt między nimi:
- sinα = sinβ;
- C = (D1 * D2 / (A + B)) * sinα = (D1 * D2 / (A + B)) * sinβ,
gdzie D1 i D2 to przekątne trapezu; α i β to kąty między nimi.
9. Wzory dla strony bocznej poprzez kąt przy dolnej podstawie i pozostałych bokach: D = (A-B) / cosα = C / sinα = H / sinα.
Ponieważ trapez o kącie prostym jest szczególnym przypadkiem trapezu, pozostałe wzory definiujące te liczby będą odpowiadały prostokątowi.

Jeżeli warunek mówi, że okrąg jest wpisany w prostokątny trapez, to można użyć następujących właściwości:
- suma podstaw jest równa sumie boków;
- odległości od wierzchołka prostokąta do punktów styczności wpisanego okręgu są zawsze równe;
- wysokość trapezu jest równa boku bocznej, prostopadłej do podstaw i równa średnicy koła;
- środek koła to punkt, w którym przecinają się dwusieczne rogów;
- jeżeli bok boczny jest podzielony przez punkt styku na segmenty H i M, to promień okręgu jest równy pierwiastkowi kwadratowemu iloczynu tych segmentów;
- czworobok utworzony przez punkty styku, wierzchołek trapezu i środek wpisanego koła - jest to kwadrat, którego bok jest równy promieniowi;
- powierzchnia figury jest równa iloczynowi podstaw i iloczynowi połowy sumy podstaw przez ich wysokość.
Ten temat jest bardzo wygodny do badania właściwości.ten geometryczny kształt. Na przykład przekątne dzielą trapez na cztery trójkąty, a te sąsiadujące z podstawami są podobne, a boki równe. To stwierdzenie można nazwać właściwością trójkątów, na które trapez jest podzielony przez jego przekątne. O pierwszej części tego stwierdzenia świadczy znak podobieństwa pod dwoma kątami. Aby udowodnić drugą część, lepiej skorzystać z poniższej metody.
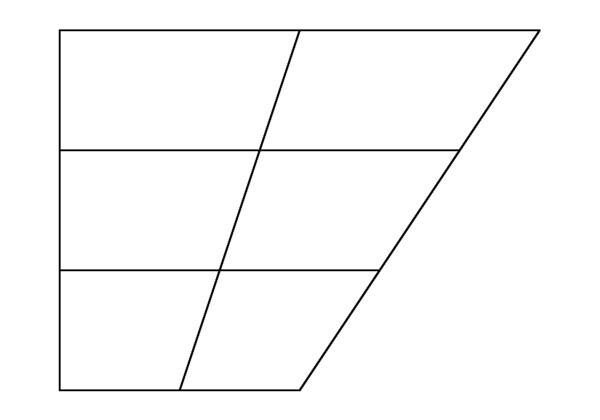
Przyjmujemy, że liczba ABSD (BP i BS to podstawa)trapez) jest podzielony przez przekątne VD i AC. Punktem ich przecięcia jest O. Otrzymujemy cztery trójkąty: AOS - u podstawy dolnej, BOS - u podstawy górnej, ABO i SOD po bokach. Trójkąty SOD i BFB mają wspólną wysokość, jeśli segmenty BO i OD są ich podstawami. Otrzymujemy, że różnica między ich obszarami (P) jest równa różnicy między tymi segmentami: PBOS / PSOD = BO / OD = K. Dlatego PSOD = PBOS / K. Podobnie trójkąty BFB i AOB mają wspólną wysokość. Za ich podstawy przyjmujemy segmenty SB i OA. Otrzymujemy PBOS / PAOB = SO / OA = K i PAOB = PBOS / K. Wynika z tego, że PSOD = PAOB.
Zaleca się utrwalenie materiału studentomznajdź połączenie między obszarami uzyskanych trójkątów, na które trapez jest podzielony przez przekątne, rozwiązując następujący problem. Wiadomo, że obszary trójkątów biofeedbacku i AOD są równe, konieczne jest znalezienie obszaru trapezu. Ponieważ PSOD = PAOB, oznacza to, że PABSD = PBOS + PAOD + 2 * PSOD. Z podobieństwa trójkątów BFB i AOD wynika, że BO / OD = √ (PBOS / PAOD). Dlatego PBOS / PSOD = BO / OD = √ (PBOS / PAOD). Otrzymujemy PSOD = √ (PBOS * PAOD). Wtedy PABSD = PBOS + PAOD + 2 * √ (PBOS * PAOD) = (√ PSOS + √ PAOD) 2.
Kontynuując rozwijanie tego tematu, można udowodnić iinne ciekawe cechy trapezów. Tak więc za pomocą podobieństwa można udowodnić właściwość odcinka, który przechodzi przez punkt utworzony przez przecięcie przekątnych tej figury geometrycznej, równoległej do podstaw. Aby to zrobić, rozwiążemy następujący problem: konieczne jest znalezienie długości odcinka RK, który przechodzi przez punkt O. Z podobieństwa trójkątów AOD i BFB wynika, że AO / OS = AD / BS . Z podobieństwa trójkątów AOR i ASB wynika, że AO / AC = RO / BS = HELL / (BS + HELL). Stąd otrzymujemy, że RO = BS * PIEKŁO / (BS + PIEKŁO). Podobnie z podobieństwa trójkątów DOK i DBS wynika, że OK = BS * HELL / (BS + HELL). Stąd otrzymujemy, że RO = OK i RK = 2 * BS * HELL / (BS + HELL). Odcinek przechodzący przez punkt przecięcia przekątnych, równoległy do podstaw i łączący oba boki, jest podzielony na pół przez punkt przecięcia. Jego długość jest średnią harmoniczną podstawy figury.
Rozważ następującą jakość trapezu, która:nazywana jest właściwością czteropunktową. Punkty przecięcia przekątnych (O), przecięcie przedłużenia boków bocznych (E), a także punkty środkowe podstaw (T i G) leżą zawsze na tej samej linii. Łatwo to udowodnić metodą podobieństwa. Otrzymane trójkąty BES i AED są podobne, aw każdym z nich mediany ET i EZ dzielą kąt w wierzchołku E na równe części. W konsekwencji punkty E, T i Ж leżą na jednej prostej. W ten sam sposób na jednej prostej leżą punkty T, O i Z. Wszystko to wynika z podobieństwa trójkątów BFB i AOD. Z tego wnioskujemy, że wszystkie cztery punkty - E, T, O i F - będą leżeć na jednej linii prostej.
Stosując takie trapezy można zasugerowaćaby uczniowie mogli znaleźć długość odcinka (LF), który dzieli figurę na dwie podobne. Ten segment musi być równoległy do podstaw. Ponieważ otrzymane trapezy ALPD i LBSF są podobne, to BS / LF = LF / BP. Wynika z tego, że LF = √ (BS * PIEKŁO). Otrzymujemy, że odcinek dzielący trapez na dwa podobne ma długość równą średniej geometrycznej długości podstaw figury.
Rozważ następującą właściwość podobieństwa.Opiera się na segmencie, który dzieli trapez na dwie równej wielkości figury. Zakładamy, że trapez ABSD jest podzielony przez odcinek na dwa podobne. Ze szczytu B spada wysokość, która jest podzielona przez odcinek EH na dwie części - B1 i B2. Otrzymujemy: PABSD / 2 = (BS + EH) * B1 / 2 = (HELL + EH) * B2 / 2 i PABSD = (BS + HELL) * (B1 + B2) / 2. Następnie tworzymy układ, którego pierwsze równanie to (BS + EH) * B1 = (AD + EH) * B2 i drugie (BS + EH) * B1 = (BS + HELL) * (B1 + B2) / 2. Wynika z tego, że B2 / B1 = (BS + EH) / (HELL + EH) i BS + EH = ((BS + HELL) / 2) * (1 + B2 / B1). Otrzymujemy, że długość odcinka dzielącego trapez na dwa równe rozmiary jest równa średniej kwadratowej długości podstaw: ((BS2 + AD2) / 2).
W ten sposób udowodniliśmy, że:
1. Odcinek łączący punkty środkowe boków bocznych w trapezie jest równoległy do BP i BS i jest równy średniej arytmetycznej BS i BP (długość podstawy trapezu).
2. Linia przechodząca przez punkt O przecięcia przekątnych równoległych do HELL i BS będzie równa średniej harmonicznej liczb HELL i BS (2 * BS * HELL / (BS + HELL)).
3. Odcinek dzielący trapez na podobne ma długość średniej geometrycznej podstaw BS i BP.
4. Element dzielący figurę na dwa równe rozmiary ma długość średniej kwadratowej liczby BP i BS.
Aby skonsolidować materiał i zrozumieć związek międzybadanych segmentów, uczeń musi je zbudować dla określonego trapezu. Potrafi z łatwością wyświetlić linię środkową i odcinek przechodzący przez punkt O - przecięcie przekątnych figury - równolegle do podstaw. Ale gdzie będą znajdować się trzecia i czwarta? Ta odpowiedź doprowadzi ucznia do odkrycia pożądanego związku między średnimi.
Rozważ następującą właściwość tego rysunku.Zakładamy, że odcinek MH jest równoległy do podstaw i dzieli przekątne na pół. Punkty przecięcia będą nazwane Ш i Ш. Odcinek ten będzie równy połowie różnicy baz. Przyjrzyjmy się temu bliżej. MSh - środkowa linia trójkąta ABS, jest równa BS / 2. MCh to środkowa linia trójkąta ABD, równa BP / 2. Następnie otrzymujemy, że SHSH = MSH-MSH, zatem SHSH = PIEKŁO / 2-BS / 2 = (PIEKŁO + VS) / 2.
Zobaczmy, jak to jest określaneten element dla danego kształtu geometrycznego. Aby to zrobić, konieczne jest przedłużenie podstaw w przeciwnych kierunkach. Co to znaczy? Konieczne jest dodanie dolnej do górnej podstawy - po obu stronach, na przykład po prawej stronie. I wydłuż dolny o długość górnego w lewo. Następnie łączymy je przekątną. Punkt przecięcia tego odcinka ze środkową linią figury jest środkiem ciężkości trapezu.
Wymieńmy cechy takich kształtów:
1. Trapez można wpisać w okrąg tylko wtedy, gdy jest równoramienny.
2. Trapez można opisać wokół okręgu, pod warunkiem, że suma długości ich podstaw jest równa sumie długości boków.
Wpisane konsekwencje koła:
1. Wysokość opisywanego trapezu jest zawsze równa dwóm promieniom.
2. Boczna strona opisywanego trapezu jest obserwowana od środka koła pod kątem prostym.
Pierwszy wniosek jest oczywisty, ale dla dowodupo drugie, wymagane jest ustalenie, że kąt SOD jest właściwy, co w rzeczywistości również nie będzie trudne. Ale znajomość tej właściwości pozwoli ci użyć trójkąta prostokątnego podczas rozwiązywania problemów.
Teraz skonkretyzujmy te konsekwencje dlatrapez równoramienny wpisany w okrąg. Otrzymujemy, że wysokość jest średnią geometryczną podstawy figury: H = 2R = √ (BS * HELL). Ćwicząc podstawową technikę rozwiązywania zadań na trapezy (zasada trzymania dwóch wysokości), student musi rozwiązać następujące zadanie. Zakładamy, że BT jest wysokością figury równoramiennej ABSD. Konieczne jest znalezienie segmentów AT i TD. Korzystając z opisanej powyżej formuły, nie będzie to trudne.
Teraz zastanówmy się, jak określić promieńkoło za pomocą obszaru opisanego trapezu. Obniżamy wysokość od góry B do podstawy PIEKŁA. Ponieważ okrąg jest wpisany w trapez, to BS + HELL = 2AB lub AB = (BS + HELL) / 2. Z trójkąta ABN znajdujemy sinα = BN / AB = 2 * BN / (BS + HELL). PABSD = (BS + PIEKŁO) * BN / 2, BN = 2R. Otrzymujemy PABSD = (BS + HELL) * R, z tego wynika, że R = PABSD / (BS + HELL).
.

Teraz pora przejść do ostatniego elementu tego geometrycznego kształtu. Zastanówmy się, jaka jest środkowa linia trapezu (M):
1. Przez podstawy: M = (A + B) / 2.
2. Przez wysokość, podstawę i narożniki:
• M = A-H * (ctgα + ctgβ) / 2;
• M = B + H * (ctgα + ctgβ) / 2.
3. Poprzez wysokość, przekątne i kąt między nimi. Na przykład D1 i D2 to przekątne trapezu; α, β - kąty między nimi:
M = D1 * D2 * sina/2H = D1 * D2 * sinp/2H.
4. Przez obszar i wysokość: M = P / N.


























