
Začátkem 19. století, geometr z Berlína, Jacob SteinerDal úkol spojit tři vesnice tak, aby jejich délka byla nejkratší. Následně zobecnil tento problém: je nutné najít bod v rovině tak, aby vzdálenost od n k ostatním bodům byla nejmenší. Ve 20. století pokračovaly práce na tomto tématu. Bylo rozhodnuto vzít několik bodů a spojit je tak, aby vzdálenost mezi nimi byla nejkratší. To je zvláštní případ studovaného problému.
Kruskalův algoritmus odkazuje na chamtivé algoritmy(nazývají se také gradient). Jejich podstatou je největší zisk na každém kroku. Ne vždy "chamtivé" algoritmy poskytují nejlepší řešení problému. Existuje teorie, která ukazuje, že jsou-li aplikovány na určité úkoly, poskytují optimální řešení. Toto je teorie matroidů. Algoritmus Kraskal odkazuje na tyto problémy.
Рассматриваемый алгоритм строит оптимальный rámeček grafu. Problém je následující. Nesměrovaný graf je uveden bez vícenásobných hran a smyček a na množině jeho hran je přiřazena funkce váhy w, která každému okraji e přiřazuje číslo - hmotnost okraje - w (e). Hmotnost každé podmnožiny sady hran je určena součtem hmotností jejích hran. Je nutné najít rám s nejmenší hmotností.
Алгоритм Краскала работает так.Nejprve jsou všechny hrany původního grafu uspořádány ve vzestupném pořadí hmotností. Rámec zpočátku neobsahuje žádné hrany, ale zahrnuje všechny vrcholy grafu. Po dalším kroku algoritmu je přidána jedna hrana k již vytvořené části rámce, což je překlenovací les. Není zvolen svévolně. Všechny okraje grafu, které nepatří k rámečku, lze nazvat červenou a zelenou. Vrcholy každého červeného okraje jsou v jedné spojené součásti lesa ve výstavbě a zelené vrcholy jsou v různých. Proto pokud tam přidáte červený okraj, objeví se cyklus a pokud je zelený, v doménové struktuře získané po tomto kroku budou připojené komponenty menší o jeden. K výsledné konstrukci tedy nelze přidat jediný červený okraj, ale lze přidat jakýkoli zelený okraj, aby se získal les. Přidá se zelené žebro s minimální hmotností. Výsledkem je rám s nejnižší hmotností.
Označte aktuální les F.Rozděluje množinu vrcholů grafu do souvisejících oblastí (jejich spojovací formy F a neprotínají se ve dvojicích). Na červených okrajích leží oba vrcholy v jedné části. Část (x) je funkce, která pro každý vrchol x vrací název části, do které x patří. Unite (x, y) je procedura, která vytváří nový oddíl, který se skládá ze spojení částí xay a všech ostatních částí. Nechť n je počet hran grafu. Všechny tyto koncepty jsou zahrnuty v Kraskalově algoritmu. Realizace:
Seřaďte všechny hrany grafu od 1. do nth ve vzestupném pořadí podle hmotnosti. (ai, bi jsou vrcholy hrany s číslem i).
pro i = 1 až n.
x: = část (ai).
y: = část (bi).
Pokud x není rovno y, pak Unite (x, y), uveďte do okraje F číslo i.
Nechť T je rámec původního grafu vytvořeného pomocí algoritmu Kruskal a S je libovolný rámec. Je nutné prokázat, že w (T) nepřesahuje w (S).
Nechť M je množina hran S, P je množina hranT. Pokud S není rovno T, pak existuje hrana et kostry T, která nepatří do S. Connect et do S. Je vytvořen cyklus, řekněme to C. Odebíráme z C všechny hrany patřící S. Získáme novou kostru, protože tam jsou také hrany a je v ní tolik vrcholů. Jeho hmotnost nepřesahuje w (S), protože w (et) je na základě Kraskalového algoritmu nejvýše w (s). Tato operace (nahrazení okrajů S hranami T) se bude opakovat, dokud nezískáme T. Hmotnost každého následujícího získaného rámce není větší než hmotnost předchozího, což znamená, že w (T) není větší než w (S).
Správnost algoritmu Kruskal také vyplývá z Rado-Edmondsovy věty o matroidech.
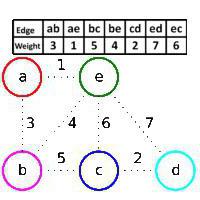
Graf s vrcholy a, b, c, d, e a hranami (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Hmotnosti žeber jsou uvedeny v tabulce a na obrázku. Zpočátku les ve výstavbě F obsahuje všechny vrcholy grafu a neobsahuje žádné hrany. Algoritmus Kraskal nejprve přidá hranu (a, e), protože má nejmenší hmotnost a vrcholy a a e jsou v různých složkách lesa F (hrana (a, e) je zelená), pak hrana (c, d), proto že tato hrana má nejmenší hmotnost hran grafu, které nepatří do F, a je zelená, pak se ze stejných důvodů přidá hrana (a, b). Ale hrana (b, e) je přeskočena, i když má nejmenší hmotnost zbývajících hran, protože je červená: vrcholy b a e patří ke stejné připojené složce lesa F, to znamená, že když přidáme hranu (b, e) k F, pak cyklus. Poté se přidá zelený okraj (b, c), přeskočí se červený okraj (c, e) a pak d, e. Hrany (a, e), (c, d), (a, b), (b, c) jsou tedy přidávány postupně. Optimální rámeček původního grafu se skládá z niherů. V tomto případě algoritmus funguje. Kraskala. Je ukázán příklad.

Obrázek ukazuje graf skládající se ze dvou připojených komponent. Tučné čáry ukazují okraje optimální struktury (zelené) vytvořené pomocí Kraskalova algoritmu.

Horní graf ukazuje původní graf a dolní ukazuje minimální hmotnostní rámec vytvořený pro daný algoritmus.
Posloupnost přidaných žeber: (1,6); (0,3), (2,6) nebo (2,6), (0,3) - na tom nezáleží; (3.4); (0,1), (1,6) nebo (1,6), (0,1) je také indiferentní (5,6).

Algoritmus Kraskal nachází praktickou aplikaci, například pro optimalizaci pokládání komunikací, silnic v nových mikrodistribucích sídel v každé zemi, stejně jako v jiných případech.


























