
V prostoru může být rovina definována různýmizpůsoby (jeden bod a vektor, dva body a vektor, tři body atd.). S ohledem na to může mít rovnice roviny různé podoby. Rovněž za určitých podmínek mohou být roviny rovnoběžné, kolmé, protínající se atd. O tom se budeme bavit v tomto článku. Naučíme se, jak vytvořit obecnou rovnici roviny, nejen.
Předpokládejme, že existuje prostor R3který má pravoúhlý souřadný systém XYZ. Definujeme vektor α, který bude uvolněn z počátečního bodu O. Koncem vektoru α nakreslíme rovinu, která je k němu kolmá.
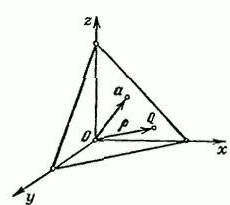
Na произвольн označíme libovolný bod Q = (x, y, z). Poloměrový vektor bodu Q napíšeme písmenem p. V tomto případě je délka vektoru a rovna p = IaI a Ʋ = (cosα, cosβ, cosy).
Toto je jednotkový vektor, na který je směrovánostrana, jako vektor a. a, p, a y jsou úhly, které jsou vytvořeny mezi vektorem Ʋ a kladnými směry os prostoru x, y, z. Projekce jakéhokoli bodu QϵP na vektor Ʋ je konstantní hodnota, která se rovná p: (p, Ʋ) = p (p≥0).
Uvedená rovnice má smysl, když p = 0.Jediná rovina П v tomto případě protne bod O (α = 0), což je počátek, a jednotkový vektor Ʋ uvolněný z bodu O bude kolmý na ,, navzdory svému směru, což znamená, že vektor Ʋ je definován přesnost ke značce. Předchozí rovnice je rovnice naší roviny P, vyjádřená ve vektorovém tvaru. Ale v souřadnicích bude jeho vzhled vypadat takto:

P je zde větší nebo rovno 0. Našli jsme rovnici roviny v prostoru v normální podobě.
Pokud vynásobíme rovnici v souřadnicích libovolným číslem, které se nerovná nule, dostaneme rovnici rovnou této rovnici definující stejnou rovinu. Vypadá to takto:

Zde A, B, C jsou čísla, která jsou současně nenulová. Tato rovnice se označuje jako obecná rovinná rovnice.
Obecná rovnice může být modifikována za přítomnosti dalších podmínek. Uvažujme některé z nich.
Předpokládejme, že koeficient A je 0. To znamená, že tato rovina je rovnoběžná s danou osou Ox. V tomto případě se změní tvar rovnice: Wu + Cz + D = 0.
Podobně se forma rovnice změní za následujících podmínek:
V případě, že čísla A, B, C, D jsou nenulová, může být rovnice (0) následující:
x / a + y / b + z / s = 1,
ve kterém a = -D / A, b = -D / B, c = -D / C.
Výsledkem je rovnice roviny v segmentech. Je třeba poznamenat, že tato rovina protne osu Ox v bodě se souřadnicemi (a, 0,0), Oy - (0, b, 0) a Oz - (0,0, s).

S ohledem na rovnici x / a + y / b + z / c = 1 je snadné vizuálně vizualizovat umístění roviny vzhledem k danému souřadnému systému.
Normální vektor n k rovině имеет má souřadnice, které jsou koeficienty obecné rovnice této roviny, tj. N (A, B, C).

K určení souřadnic normálu n stačí znát obecnou rovnici dané roviny.
При использовании уравнения в отрезках, которое má tvar x / a + y / b + z / s = 1, protože při použití obecné rovnice můžete zapsat souřadnice libovolného normálního vektoru dané roviny: (1 / a + 1 / b + 1 / s).
Stojí za zmínku, že normální vektor pomáhářešit různé úkoly. Nejběžnější jsou úkoly spočívající v prokázání kolmosti nebo rovnoběžnosti letadel, problémů s hledáním úhlů mezi rovinami nebo úhlů mezi rovinami a přímkami.
Nenulový vektor n, kolmý na danou rovinu, se pro danou rovinu nazývá normální (normální).
Předpokládejme, že v souřadnicovém prostoru (pravoúhlý souřadný systém) daný Oxyz:

Je nutné vytvořit rovnici pro rovinu, která bude procházet bodem Mₒ kolmým na normální n.
Ve vesmíru volíme libovolný bod aoznačíme to M (xy, z). Nechť vektor rádiusu každého bodu M (x, y, z) je r = x * i + y * j + z * k a vektor rádiusu bodu Mₒ (xₒ, yₒ, zₒ) - rₒ = xₒ * i + yₒ * j + zₒ * k. Bod M patří do dané roviny, pokud je vektor MₒM kolmý na vektor n. Píšeme podmínku ortogonality pomocí skalárního součinu:
[MₒM, n] = 0.
Protože МₒМ = r - rₒ, bude vektorová rovnice roviny vypadat takto:
[r - rₒ, n] = 0.
Tato rovnice může mít jinou podobu.K tomu se použijí vlastnosti skalárního součinu a transformuje se levá strana rovnice. [r - rₒ, n] = [r, n] - [rₒ, n]. Pokud je [rₒ, n] označeno jako c, získá se následující rovnice: [r, n] - c = 0 nebo [r, n] = c, která vyjadřuje stálost projekcí na normální vektor poloměrových vektorů daných bodů, které patří do roviny.
Nyní můžeme získat souřadnicovou formu vektorové rovnice naší roviny [r - rₒ, n] = 0. Protože r - rₒ = (х - хₒ) * i + (у - у у) * j + (z - zₒ) * k, a n = A * i + B * j + C * k, máme:

Ukázalo se, že máme rovnici roviny procházející bodem kolmým na normální n:
A * (x-xₒ) + B * (y - yₒ) С * (z - zₒ) = 0.
Definujeme dva libovolné body M '(x', y ', z') a M ″ (x ″, y ″, z ″), jakož i vektor a (a ', a ″, a ‴).
Nyní můžeme nakreslit rovnici pro danou rovinu, která bude procházet dostupnými body M 'a M ″, jakož i libovolným bodem M se souřadnicemi (x, y, z) rovnoběžnými s daným vektorem a.
Navíc vektory M'M = {x-x '; y-y'; zz 'a M ″ M = {x ″ -x'; y ″ -y '; z ″ -z' а = (а ′, а ″, а ‴), což znamená, že (М′М, М ″ М, а) = 0.
Naše rovnice letadla ve vesmíru bude tedy vypadat takto:
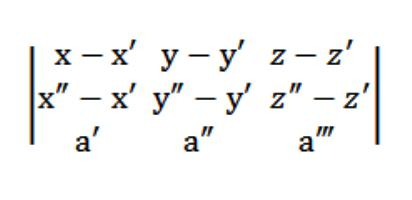
Řekněme, že máme tři body:(x ', y', z '), (x ″, y ″, z ″), (x ‴, y ‴, z ‴), které nepatří do jednoho řádku. Je nutné napsat rovnici roviny procházející danými třemi body. Teorie geometrie tvrdí, že tento druh letadla skutečně existuje, pouze je jediný. Protože tato rovina protíná bod (x, y, z), bude forma její rovnice následující:

Zde A, B, C jsou nenulové současně. Daná rovina také protíná dva další body: (x ″, y ″, z ″) a (x ‴, y ‴, z ‴). V tomto ohledu musí být tyto podmínky splněny:

Nyní můžeme sestavit homogenní soustavu rovnic (lineárních) s neznámými u, v, w:

V našem případě je x, y nebo z libovolnébod, který splňuje rovnici (1). Při dané rovnici (1) a systému rovnic (2) a (3) vyhovuje soustava rovnic na obrázku výše vektoru N (A, B, C), který je netriviální. Proto je determinant tohoto systému nulový.
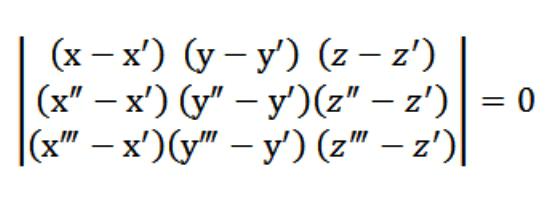
Rovnice (1), kterou jsme získali, je aexistuje rovinná rovnice. Přes 3 body to rozhodně prochází, a to lze snadno ověřit. Abychom to mohli udělat, musíme rozšířit náš determinant podle prvků v prvním řádku. Z existujících vlastností determinantu vyplývá, že naše rovina protíná současně tři původně dané body (x, y, z), (x, y, z,), (x, y, z). To znamená, že jsme vyřešili úkol před námi.
Úhel v úhlu jeprostorová geometrická figura tvořená dvěma polorovinami, které pocházejí z jedné přímky. Jinými slovy, toto je část prostoru, která je těmito poloplanemi omezena.
Předpokládejme, že máme dvě roviny s následujícími rovnicemi:
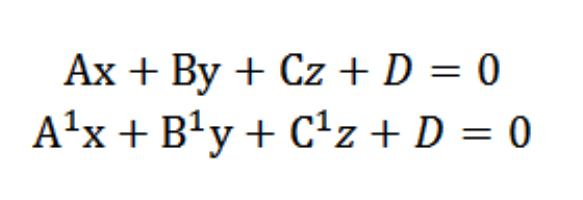
Víme, že vektory N = (A, B, C) aN1 = (А¹, В¹, С¹) jsou kolmé podle daných rovin. V tomto ohledu je úhel φ mezi vektory N a N1 roven úhlu (dihedral), který je umístěn mezi těmito rovinami. Skalární produkt má tvar:
NN¹ = | N || N¹ | cos φ,
právě proto
cosφ = NN1 / | N || N1 | = (AA1 + BB1 + CC1) / ((√ (А² + ²² + С²)) * (√ (А¹) ² + (¹) ² + (¹) ²)).
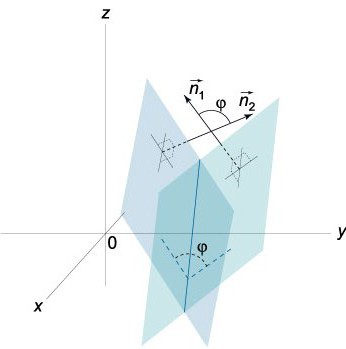
Stačí vzít v úvahu, že 0≤φ≤π.
Ve skutečnosti dvě roviny, které se protínají, tvoří dva úhly (dihedral): φ1 a φ2. Jejich součet je π (φ1+ φ2= π). Co se týče jejich kosinů, jejich absolutní hodnoty jsou stejné, liší se však ve známkách, tj. Cos φ1= -cos φ2. Pokud nahradíme A, B a C v rovnici (0) čísly -A, -B a -C, potom rovnice, kterou dostaneme, určí stejnou rovinu, jediný úhel φ v rovnici cos φ = NN1/ | N || N1| bude nahrazeno π-φ.
Kolmé se nazývají roviny mezi nimikterý úhel je 90 stupňů. Pomocí výše popsaného materiálu můžeme najít rovnici roviny kolmé k druhé. Předpokládejme, že máme dvě roviny: Ax + Vu + Cz + D = 0 a A¹x + B¹u + C¹z + D = 0. Můžeme říci, že budou kolmé, pokud cosφ = 0. To znamená, že NN 1 = AA 1 + BB 1 + CC 1 = 0.
Paralelní se nazývají dvě roviny, které neobsahují společné body.
Podmínka rovnoběžnosti letadel (jejich rovnicestejné jako v předchozím odstavci) je to, že vektory N a N1, které jsou na ně kolmé, jsou kolineární. A to znamená, že jsou splněny následující podmínky proporcionality:
А / А¹ = В / В¹ = С / С¹.
Pokud jsou podmínky proporcionality rozšířeny - A / А¹ = В / В¹ = С / С¹ = DD¹,
to znamená, že se tyto letouny shodují. A to znamená, že rovnice Ax + Vy + Cz + D = 0 a А¹х + В¹у + С¹z + D¹ = 0 popisují jednu rovinu.
Předpokládejme, že máme rovinu P, která je dánarovnice (0). Je nutné najít vzdálenost od bodu se souřadnicemi (xₒ, yₒ, zₒ) = Qₒ. K tomu musíte uvést rovnici roviny P do normální podoby:
(ρ, v) = p (p≥0).
V tomto případě je ρ (x, y, z)poloměrový vektor našeho bodu Q umístěný na P, p je délka kolmého P, která byla uvolněna z nulového bodu, v je jednotkový vektor, který je umístěn ve směru a.

Rozdíl ρ-ρº poloměrového vektoru určitého bodu Q = (x, y, z) patřícího k П, jakož i poloměrový vektor daného bodu Q0= (xₒ, yₒ, zₒ) je vektor, jehož absolutní hodnota projekce na v se rovná vzdálenosti d, která musí být nalezena od Q0= (xₒ, yₒ, zₒ) do:
D = | (ρ-ρ0, v) |, ale
(ρ-ρ0, v) = (ρ, v) - (ρ0, v) = р– (ρ0, v).
Tak se ukázalo
d = | (ρ0, v) -p |.
Nyní je vidět výpočet vzdálenosti d od Q0 do roviny П, musíte použít normální tvar rovnice roviny, zatímco se přenesete na levou stranu p a dosadíte (xₒ, yₒ, zₒ) na poslední místo x, y, z.
Najdeme tedy absolutní hodnotu výsledného výrazu, tj. Požadovaný d.
Použitím parametrického jazyka získáme zřejmé:
d = | Axₒ + Byₒ + Czₒ | / √ (A² + B² + C²).
Pokud daný bod Q0 je na druhé straně roviny P, jako počátek, pak mezi vektorem ρ-ρ0 a v je tupý úhel, proto:
d = - (ρ-ρ0, v) = (ρ0, v) -p> 0.
V případě, že bod Q0 spolu s počátkem souřadnic se nachází na stejné straně P, pak je vytvořený úhel ostrý, to znamená:
d = (ρ-ρ0, v) = p - (str0, v)> 0.
Ve výsledku se ukázalo, že v prvním případě (ρ0, v)> р, ve druhém (ρ0, v) <str.
Tečná rovina k povrchu v bodě tečnosti Mº je rovina obsahující všechny možné tečny ke křivkám nakresleným tímto bodem na povrchu.
S touto formou rovnice povrchu F (x, y, z) = 0 bude rovnice tečné roviny v tečném bodě M (x, y, z) vypadat takto:
Fx(xº, yº, zº) (x- xº) + Fx(xº, yº, zº) (y-yº) + Fx(xº, yº, zº) (z-zº) = 0.
Pokud nastavíme povrch ve explicitní podobě z = f (x, y), bude tečná rovina popsána rovnicí:
z-zº = f (xº, yº) (x- xº) + f (xº, yº) (y-yº).
Systém je umístěn v trojrozměrném prostorusouřadnice (obdélníkové) Oxyz, jsou uvedeny dvě roviny P ′ a P ″, které se protínají a neshodují. Protože libovolná rovina v pravoúhlém souřadném systému je určena obecnou rovnicí, budeme předpokládat, že P ′ a P ″ jsou dány rovnicemi Ax + B′y + C′z + D ′ = 0 a A „x + B“ y + C „z + D“ = 0. V tomto případě máme normální n '(A', B ', C') roviny P 'a normální n' (A ', B', C ') roviny P'. Protože naše roviny nejsou rovnoběžné a neshodují se, nejsou tyto vektory kolineární. Pomocí matematického jazyka můžeme tuto podmínku napsat následovně: n ′ ≠ n ″ ↔ (A ′, B ′, C ′) ≠ (λ * A ″, λ * B ″, λ * C ″), λϵR. Nechť přímka, která leží na průsečíku P ′ a P ″, bude označena písmenem a, v tomto případě a = P ′ ∩ P ″.
a je přímka skládající se ze sady všech bodů(společné) roviny P 'a P ″. To znamená, že souřadnice libovolného bodu patřícího k přímce a musí současně splňovat rovnice A'x + B'y + C'z + D '= 0 a A ″ x + B ″ y + C ″ z + D ″ = 0. To znamená, že souřadnice bodu budou konkrétním řešením následující soustavy rovnic:

Ve výsledku se ukazuje, že řešení (obecné) tohotosoustava rovnic určí souřadnice každého z bodů přímky, která bude fungovat jako průsečík P ′ a P ″, a určí přímku a v souřadnicovém systému Oxyz (obdélníkový) v prostoru.


























