Binære relationer og deres egenskaber

En bred vifte af relationer som eksemplificeret ved sætledsaget af et stort antal koncepter, der starter med deres definitioner og slutter med en analytisk analyse af paradokser. Mangfoldigheden af ​​det koncept, der diskuteres i artiklen, er uendelig på et sæt. Selvom de taler om binære forhold mellem flere mængder, når de taler om to typer. Og også mellem genstande eller udsagn.

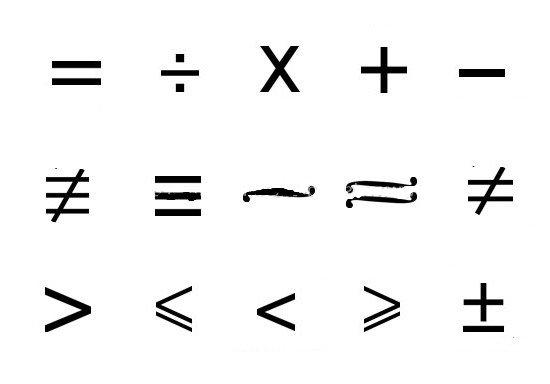
Typisk betegnes binære forholdsymbol R, det vil sige, hvis xRx for en værdi x fra feltet R, kaldes en sådan egenskab refleksiv, hvor x og x er accepterede tankeobjekter, og R fungerer som et tegn på en eller anden form for forhold mellem individer. På samme tid, hvis vi udtrykker xRy® eller yRx, indikerer dette en symmetri-tilstand, hvor ® er et implikationstegn, der ligner konjunktionen "hvis ..., så ..." Og til sidst dekodning af inskriptionen (xRy Ùy Rz) ®xRz fortæller dig om et transitivt forhold, og Ù-tegnet er en sammenhæng.

En binær relation, der sker på samme tidrefleksiv, symmetrisk og transitiv, kaldes det et ækvivalensforhold. Forholdet f er en funktion, og fra Î f og Î f følger det at y = z. En simpel binær funktion kan let anvendes til to enkle argumenter i en bestemt rækkefølge, og kun i dette tilfælde giver den den en mening rettet mod disse to udtryk, taget i et bestemt tilfælde.

Det skal siges, at f kortlægger x til y,

Baseret på ovenstående bestemmes ækvivalensforholdene for binære relationer af egenskaberne:

• refleksivitet - forhold (M ~ N);
• symmetri - hvis ligheden er M ~ N, vil der være N ~ M;
• transitivitet - hvis to ligheder M ~ N og N ~ P, så som et resultat M ~ P.

Overvej de deklarerede egenskaber ved binære relationermere detaljeret. Refleksivitet er en af ​​egenskaberne ved nogle forbindelser, hvor hvert element i det studerede sæt er i en given ligestilling til sig selv. For eksempel er antallet a = c og a³ c refleksive forbindelser, fordi altid a = a, c = c, a³ a, c³ c. På samme tid er ulighedsforholdet a> c antirefleksivt på grund af umuligheden af ​​eksistensen af ​​uligheden a> a. Denne egenskabs aksiom kodes af tegn: aRc® aRa Ù cRc, her betyder symbolet ® ordet "indebærer" (eller "implicerer"), og tegnet Ù - fungerer som en forening "og" (eller sammenhæng). Det følger af denne erklæring, at hvis dommen aRc er sand, er udtrykkene aRa og cRc også sande.

Symmetri indebærer et forholdog i tilfælde af, at mentale objekter udskiftes, det vil sige med et symmetrisk forhold, fører permutationen af ​​objekter ikke til en transformation af formen "binære relationer". For eksempel er forholdet mellem lighed a = c symmetrisk på grund af ækvivalensen af ​​forholdet c = a; dommen a¹c er også den samme, da den svarer til forbindelsen med¹a.

Et transitivt sæt er sådan en egenskab forder opfylder følgende krav: y Î x, z Î y ® z Î x, hvor ® er et tegn, der erstatter ordene: "hvis ..., så ...". Formlen læses verbalt som følger: "Hvis y afhænger af x, hører z til y, afhænger z også af x."