
En af de vigtigste videnskaber, hvis anvendelse kan væreset i discipliner som kemi, fysik og endda biologi er matematik. Studiet af denne videnskab giver dig mulighed for at udvikle nogle mentale kvaliteter, forbedre abstrakt tænkning og evnen til at koncentrere dig. Et af de emner, der fortjener særlig opmærksomhed i kurset "Matematik", er addition og subtraktion af brøker. Mange studerende har svært ved at studere det. Måske hjælper vores artikel dig med bedre at forstå dette emne.
Brøker er de samme tal, som du kan brugeudføre forskellige handlinger. De adskiller sig fra heltal i nærværelse af en nævner. Derfor skal du studere nogle af deres funktioner og regler, når du udfører handlinger med brøker. Det enkleste tilfælde er subtraktion af almindelige fraktioner, hvis nævnere er repræsenteret som det samme antal. Denne handling vil ikke være vanskelig, hvis du kender en simpel regel:
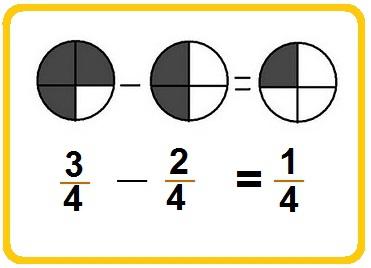
Lad os se, hvordan det ser ud med et eksempel:
7/19 - 3/19 = (7 - 3) / 19 = 4/19.
Træk fra tælleren af fraktionen "7"tælleren for den fratrukkede brøkdel er "3", vi får "4". Vi skriver dette tal i tælleren af svaret, og i nævneren sætter vi det samme tal, der var i nævnerne for den første og anden brøk - "19".
Billedet nedenfor viser nogle flere lignende eksempler.

Overvej et mere komplekst eksempel, hvor fraktioner med de samme nævnere trækkes fra:
29/47 - 3/47 - 8/47 - 2/47 - 7/47 = (29 - 3 - 8 - 2 - 7) / 47 = 9/47.
Fra tælleren af den reducerede brøkdel "29" ved at trække medkøtællere af alle efterfølgende fraktioner - "3", "8", "2", "7". Som et resultat får vi resultatet "9", som vi skriver i tælleren af svaret, og i nævneren skriver vi det antal ned, der er i nævnerne for alle disse fraktioner - "47".
Tilsætning og subtraktion af almindelige fraktioner udføres efter samme princip.
Lad os se, hvordan det ser ud med et eksempel:
1/4 + 2/4 = 3/4.
Til tælleren for den første periode af brøken - "1" -tilføj tælleren til den anden sigt af brøkdelen - "2". Resultatet - "3" - er skrevet i tælleren af summen, og nævneren er den samme som i brøkene - "4".

Handling med fraktioner, der har det sammenævneren, har vi allerede overvejet. Som du kan se, ved at kende de enkle regler, er det ret nemt at løse sådanne eksempler. Men hvad hvis du har brug for at udføre en handling med brøker, der har forskellige nævnere? Mange gymnasieelever er forvirrede af disse eksempler. Men selv her, hvis du kender løsningsprincippet, vil eksemplerne ikke længere være vanskelige for dig. Der er også en regel her, uden hvilken løsningen af sådanne fraktioner simpelthen er umulig.
For at trække fraktioner med forskellige nævnere er det nødvendigt at bringe dem til den samme laveste nævner.

Vi vil tale mere om, hvordan du gør dette.
For at bringe flere fraktioner tilden samme nævner, skal du bruge brøkens hovedegenskab i løsningen: efter at have divideret eller ganget tælleren og nævneren med det samme tal, får du en brøkdel, der er lig med den givne.
Så for eksempel kan fraktionen 2/3 have sådannævnere som "6", "9", "12" osv., dvs. det kan have form af et hvilket som helst tal, der er et multiplum af "3". Når vi gange tælleren og nævneren med "2", får vi brøkdelen 4/6. Når vi har multipliceret tælleren og nævneren for den originale brøkdel med "3", får vi 6/9, og hvis den samme handling udføres med tallet "4", får vi 8/12. Med en lighed kan det skrives således:
2/3 = 4/6 = 6/9 = 8/12 ...
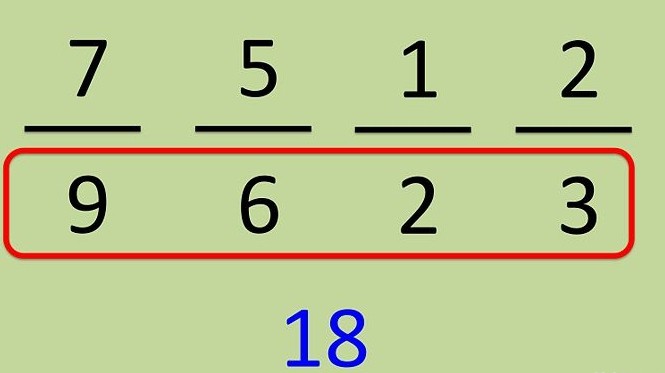
Overvej hvordan man reducerer flere fraktioner tilden samme nævneren. Lad os for eksempel tage de fraktioner, der er vist på billedet nedenfor. Først skal du bestemme, hvilket nummer der kan blive nævneren for dem alle. For at gøre det nemmere faktoriserer vi de tilgængelige nævnere.
Nævneren for brøkdel 1/2 og brøkdel 2/3 efter faktorerdu kan ikke nedbrydes. Nævneren 7/9 har to faktorer 7/9 = 7 / (3 x 3), nævneren for fraktionen 5/6 = 5 / (2 x 3). Nu skal du bestemme, hvilke faktorer der vil være den mindste for alle disse fire fraktioner. Da den første brøkdel i nævneren indeholder tallet "2", hvilket betyder, at det skal være til stede i alle nævnere, er der to tredobler i 7/9 fraktionen, hvilket betyder, at begge også skal være til stede i nævneren. I betragtning af ovenstående bestemmer vi, at nævneren består af tre faktorer: 3, 2, 3 og er lig med 3 x 2 x 3 = 18.
Overvej den første fraktion - 1/2. Dens nævner indeholder "2", men der er ikke et enkelt ciffer "3", men der skal være to. For at gøre dette multiplicerer vi nævneren med to tredobler, men ifølge brøkens egenskab skal vi også gange tælleren med to tredobler:
1/2 = (1 x 3 x 3) / (2 x 3 x 3) = 9/18.
På samme måde udfører vi handlinger med de resterende fraktioner.
Sammen ser det s

Som nævnt ovenfor, for attilføj eller træk fraktioner med forskellige nævnere, de skal reduceres til den samme nævner, og brug derefter reglerne for at trække fraktioner med den samme nævneren, som allerede er beskrevet.
Lad os se på et eksempel: 4/18 - 3/15.
Find et multiplum af 18 og 15:
Efter nævneren er fundet,det er nødvendigt at beregne en faktor, der vil være forskellig for hver brøk, det vil sige det antal, hvormed det vil være nødvendigt at multiplicere ikke kun nævneren, men også tælleren. For at gøre dette divideres det antal, vi fandt (det fælles multiplum) med nævneren for den brøkdel, som yderligere faktorer skal bestemmes for.
Det næste trin i vores løsning er at bringe hver brøkdel til nævneren "90".
Vi har allerede diskuteret, hvordan dette gøres. Lad os se, hvordan dette er skrevet i et eksempel:
(4 x 5) / (18 x 5) - (3 x 6) / (15 x 6) = 20/90 - 18/90 = 2/90 = 1/45.
Hvis brøkene er med små tal, kan fællesnævner bestemmes som i eksemplet vist på billedet nedenfor.

Tilsætningen af fraktioner med forskellige nævnere udføres på samme måde.
Vi har allerede dækket fratrækningen af fraktioner og deres tilføjelse i detaljer. Men hvordan trækker du fra, hvis fraktionen har et heltal? Lad os igen bruge et par regler:

Der er en anden måde, hvorpå du kanudføre addition og subtraktion af fraktioner med hele dele. Til dette udføres handlinger separat med hele dele og separat handlinger med brøker, og resultaterne registreres sammen.

Ovenstående eksempel består af fraktioner, derhar den samme nævneren. I tilfælde af at nævnerne er forskellige, skal de reduceres til det samme og derefter udføre handlingerne som vist i eksemplet.
En anden af de forskellige handlinger med fraktionerer tilfældet, når fraktionen skal trækkes fra et naturligt tal. Ved første øjekast synes et sådant eksempel vanskeligt at løse. Alt er dog ret simpelt her. For at løse det er det nødvendigt at konvertere et heltal til en brøkdel og med samme nævneren, som er i den fratrukkede brøk. Dernæst udfører vi en subtraktion svarende til subtraktion med de samme nævnere. For eksempel ser det sådan ud:
7 - 4/9 = (7 x 9) / 9 - 4/9 = 53/9 - 4/9 = 49/9.
Subtraktion af fraktioner (6klasse) er grundlaget for at løse mere komplekse eksempler, som er dækket i efterfølgende klasser. Kendskab til dette emne bruges efterfølgende til at løse funktioner, afledte osv. Derfor er det meget vigtigt at forstå og forstå handlingerne med de fraktioner, der er diskuteret ovenfor.


























