
Es gibt mehrere grundlegende Lösungsalgorithmen.Array-Sortieraufgaben. Eine der bekanntesten ist das Sortieren nach Beilagen. Aufgrund seiner Klarheit und Einfachheit, aber geringen Effizienz, wird dieses Verfahren hauptsächlich im Programmierunterricht verwendet. Es ermöglicht Ihnen, die grundlegenden Sortiermechanismen zu verstehen.
Die Essenz des Einfügungssortieralgorithmus istdie Tatsache, dass innerhalb des Quell-Arrays ein Segment nach Bedarf angeordnet ist. Jedes Element wird einzeln mit dem getesteten Teil verglichen und an Ort und Stelle eingefügt. Nachdem Sie alle Elemente aufgelistet haben, werden sie in der richtigen Reihenfolge angeordnet.
Die Reihenfolge der Auswahl der Elemente kann beliebig seinSie können beliebig oder nach einem Algorithmus ausgewählt werden. Am häufigsten wird eine sequenzielle Aufzählung ab dem Beginn des Arrays verwendet, bei der ein geordnetes Segment gebildet wird.
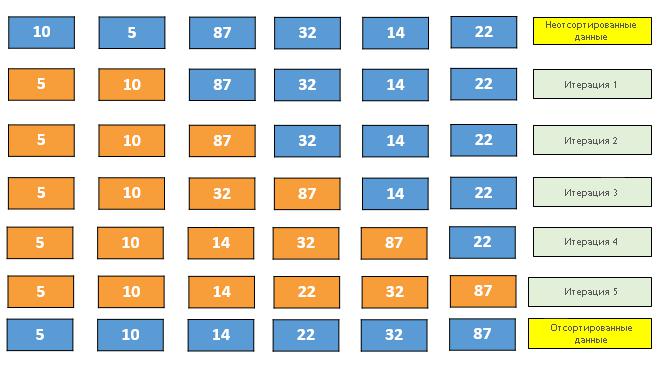
Der Beginn der Sortierung könnte folgendermaßen aussehen:
Und so weiter bis zum Ende des ursprünglichen Arrays.
Der Übersichtlichkeit halber sei ein Beispiel gegeben, wie dieser Sortiermechanismus im Alltag eingesetzt wird.
Nehmen Sie zum Beispiel eine Brieftasche.Im Banknotenfach sind Hunderte, Fünfhunderttausendstel der Banknoten durcheinander. Dies ist ein Durcheinander, in einem solchen Durcheinander ist es schwierig, sofort das richtige Stück Papier zu finden. Eine Reihe von Notizen muss sortiert werden.
Die allererste ist eine Banknote von 1000 Rubel, und unmittelbar danach - 100. Wir nehmen hundert und legen sie vor. Der dritte in einer Reihe - 500 Rubel, der richtige Ort für sie ist zwischen hundert und tausend.
Auf die gleiche Weise sortieren wir die erhaltenen Karten, wenn wir den "Narren" spielen, damit es einfacher ist, sie zu navigieren.

Die Einfügesortierungsmethode akzeptiert Eingabendas zu bestellende Quell-Array, die Vergleichsfunktion und ggf. die Funktion, die die Regel für die Aufzählung von Elementen definiert. Am häufigsten wird stattdessen der übliche Schleifenoperator verwendet.
Das erste Element an sich ist eine geordnete Menge, daher beginnt der Vergleich mit dem zweiten.
Ein Algorithmus verwendet häufig eine Hilfsfunktion, um zwei Werte auszutauschen (Swap). Es wird eine zusätzliche temporäre Variable verwendet, die Speicher benötigt und den Code etwas verlangsamt.
Die Alternative ist die MassengruppenverschiebungElemente und das anschließende Einfügen des Stroms in den frei gewordenen Raum. In diesem Fall erfolgt der Übergang zum nächsten Element, wenn der Vergleich ein positives Ergebnis liefert, das die richtige Reihenfolge angibt.

Die konkrete Implementierung hängt stark von der verwendeten Programmiersprache, ihrer Syntax und ihren Strukturen ab.
Eine klassische C-Implementierung, bei der eine temporäre Variable zum Austausch von Werten verwendet wird:
int i, j, temp;
für (i = 1; i = 0; j--)
{
if (array [j] PHP-Implementierung:
Funktion Einfügung_Sort (& $ a) {
für ($ i = 1; $ i = 0 && $ a [$ j]> $ x; $ j--) {
$ a [$ j + 1] = $ a [$ j];
}
$ a [$ j + 1] = $ x;
}
} Hier werden zuerst alle Elemente, die die Sortierbedingung nicht erfüllen, nach rechts verschoben und dann das aktuelle Element in den freigegebenen Raum eingefügt.
Java-Code mit einer while-Schleife:
Public Static Void InsertionSort (int [] arr){
für (int i = 1; i = 0 && arr [prevKey]> currElem) {
arr [prevKey + 1] = arr [prevKey];
arr [prevKey] = currElem;
prevKey--;
}
}
} Die allgemeine Bedeutung des Codes bleibt unverändert: Jedes Element des Arrays wird sequentiell mit den vorherigen verglichen und bei Bedarf an anderer Stelle mit ihnen verglichen.
Offensichtlich im besten Fall die EingabeDer Algorithmus ist bereits korrekt angeordnet. In dieser Situation muss der Algorithmus einfach jedes Element überprüfen, um sicherzustellen, dass es ohne Austausch an seinem Platz steht. Somit hängt die Laufzeit direkt von der Länge des ursprünglichen Arrays O (n) ab.
Der schlimmste Fall der Eingabe ist ein Array,in umgekehrter Reihenfolge sortiert. Es wird eine große Anzahl von Permutationen erfordern, die Laufzeitfunktion wird von der Anzahl der quadrierten Elemente abhängen.
Die genaue Anzahl der Permutationen für ein absolut ungeordnetes Array kann mit folgender Formel berechnet werden:
n * (n-1) / 2Dabei ist n die Länge des ursprünglichen Arrays. Somit sind 4950 Permutationen erforderlich, um 100 Elemente in der richtigen Reihenfolge anzuordnen.
Die Einfügemethode ist sehr effektiv zum Sortieren kleiner oder teilweise geordneter Arrays. Es wird jedoch aufgrund der hohen Komplexität der Berechnungen nicht empfohlen, überall verwendet zu werden.
Der Algorithmus wird als Hilfsmittel bei vielen anderen komplexeren Sortiermethoden verwendet.

Der Einfügealgorithmus bezieht sich auf das sogenannteNachhaltiges Sortieren. Dies bedeutet, dass nicht dieselben Elemente ausgetauscht werden, sondern die ursprüngliche Reihenfolge beibehalten wird. Der Stabilitätsindex ist in vielen Fällen wichtig für eine ordnungsgemäße Bestellung.

Das Obige ist ein großartiges visuelles Beispiel für das Sortieren von Einfügungen in einem Tanz.


























