Kuinka löytää paraboolin huippu ja rakentaa se

Matematiikassa on joukko identiteettiämissä merkittävässä paikassa on kvadratiyhtälöt. Tällaiset yhtälöt voidaan ratkaista sekä erikseen että kaavioiden piirtämiseksi koordinaattiakselille. Kvadraattisten yhtälöiden juuret ovat parabolan ja suoran viivan leikkauspisteet.

Yleinen näkymä

ah² + bx + c = 0

Roolissa "X" voidaan pitää yksittäisinä muuttujina tai kokonaisina lausekkeina. Esimerkiksi:

2²+ 5x-4 = 0;

(x + 7)²+3 (x + 7) + 2 = 0.

Tapauksessa, jossa lausekkeella on x: n rooli, on välttämätöntä esittää se muuttujana ja löytää yhtälön juuret. Sen jälkeen samataan polynomi heihin ja löydä x.

Joten, jos (x + 7) = a, niin yhtälö on muoto a²+ 3a + 2 = 0.

D = 3²-4 * 1 * 2 = 1;

ja₁= (- 3-1) / 2 * 1 = -2;

ja₂= (- 3 + 1) / 2 * 1 = -1.

Juurten ollessa yhtä suuri kuin -2 ja -1, saadaan seuraava:

x + 7 = -2 ja x + 7 = -1;

x = -9 ja x = -8.

Miten löytää parabolan yläosa

Palataan takaisin alkuperäiseen yhtälöön. Jotta vastataan kysymykseen siitä, kuinka löytää paraboolin yläosa, sinun on tiedettävä seuraava kaava:

kanssa_sn= -b / 2a,

missä x_snon halutun pisteen x-koordinaatti.

Mutta miten löytää parabolin kärki ilman y-koordinaattiarvoa? Korvaamme saadun x-arvon yhtälöön ja löydämme halutun muuttujan. Ratkaise esimerkiksi seuraava yhtälö:

x²+ 3x-5 = 0

Löydämme parabolin kärjen x-koordinaatin arvon:

x_sn= -b / 2a = -3 / 2 * 1;

x_sn= -1,5.

Löydä parabolin kärkipisteen y-koordinaatin arvo:

y = 2x²+ 4x-3 = (- 1,5)²+3 * (- 1,5) -5;

y = -7,25.

Seurauksena on, että parabolin kärki on pisteessä, jossa on koordinaatit (-1,5; -7,25).

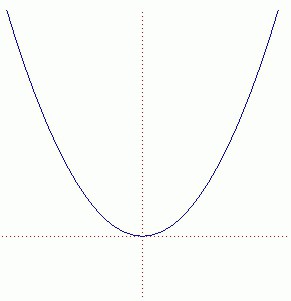
Parabolan rakentaminen

On syytä kiinnittää erityistä huomiota kvadraattisen yhtälön kertoimiin.

Kerroin a vaikuttaa parabolin suuntaan. Tapauksessa, jolla sillä on negatiivinen arvo, oksat suunnataan alaspäin ja positiivisella merkinnällä.

Kerroin b osoittaa, kuinka leveä parabolaholkki tulee olemaan. Mitä suurempi sen arvo, sitä laajempi se on.

Kerroin c osoittaa paraboolin siirtymisen OS: n akselia pitkin alkuperästä.

Olemme jo oppineet, kuinka löytää paraboolin yläosa ja löytää juuret, seuraavien kaavojen avulla:

D = b²-4ac,

missä D on erotin, joka tarvitaan yhtälön juurten löytämiseksi.

kanssa₁= (- b + V^-D) / 2a

kanssa₂= (- b-V^-D) / 2a

Tuloksena olevat x-arvot vastaavat nolla y-arvoa, koska ne ovat leikkauspisteet akselin OX kanssa.

Sen jälkeen merkitsemme koordinaattitasolleparaboolin yläosa ja saadut arvot. Tarkempi kaavio edellyttää, että löydät vielä muutama piste. Voit tehdä tämän valitsemalla minkä tahansa määritelmäalueen salliman x-arvon ja korvata sen funktion yhtälössä. Laskelmien tulos on pisteen koordinaatti op-amp-akselia pitkin.

Voit yksinkertaistaa kuvaajaprosessiavedä pystysuora viiva parabolin yläosan läpi ja kohtisuorassa akseliin OX nähden. Tämä on symmetria-akseli, jonka avulla, jolla on yksi piste, voit nimetä toisen, yhtä etäisyyden päässä piirretystä viivasta.