Ominaisuudet ja menetelmät neliömäisen yhtälön juurten löytämiseksi

Maailma on suunniteltu niin, että suuri määrä päätöksiätehtävät pelkistetään toissijaisen yhtälön juurten löytämiseksi. Yhtälöiden juuret ovat tärkeitä erilaisten lakien kuvaamisessa. Tämä oli muinaisen Babylonin tutkijoiden tiedossa. Tähtitieteilijät ja insinöörit myös pakotettiin ratkaisemaan tällaiset ongelmat. Intialainen tutkija Ariabhata kehitti jo 6. vuosisadalla jKr. Perustan toissijaisen yhtälön juurten löytämiseksi. Kaavat saivat lopullisen ilmeen 1800-luvulla.

Yleiset käsitteet

Ehdotamme, että tutustu kvadraattisten yhtälöiden peruslakeihin. Yleensä tasa-arvo voidaan kirjoittaa seuraavasti:

ah² + bx + c = 0,

Toisen asteen yhtälön juurten lukumäärä voi olla yhtä tai kahta. Nopea analyysi voidaan tehdä syrjivien käsitteen avulla:

D = b² - 4ac

Lasketusta arvosta riippuen saamme:

• D> 0: lla on kaksi erilaista juuria. Yleinen kaava neliömäisen yhtälön juurten määrittämiseksi näyttää (-b ± √D) / (2a).
• D = 0, tässä tapauksessa juuri on yksi ja vastaa arvoa x = -b / (2a)
• D <0, erottajan negatiivisella arvolla, yhtälölle ei ole ratkaisua.

Huomaa: jos erotin on negatiivinen, yhtälöllä ei ole juuria vain reaalilukujen alueella. Jos algebra laajennetaan käsitteeksi monimutkaiset juuret, niin yhtälöllä on ratkaisu.

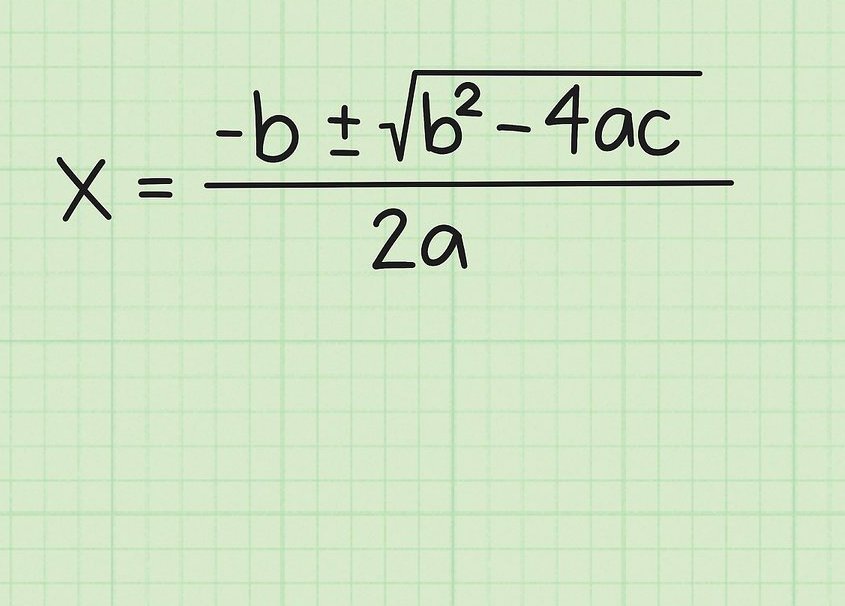
Annamme toimintaketjun, joka vahvistaa kaavan juurten löytämiseksi.

Yhtälön yleisestä muodosta seuraa:

ah² + bx = -c

Kerrotaan oikea ja vasen puoli 4a: lla ja lisätään b²saamme

ca²kanssa² + 4abx + b² = -4ac + b²

Muunna vasen puoli polynomin neliöksi (2ax b)². Otamme neliöjuuren yhtälön 2ax + b = -b ± √ (-4ac + b) molemmilta puolilta²), siirrämme kerroin b oikealle puolelle, saamme:

2ax = -b ± √ (-4ac + b²)

Tästä seuraa:

x = (-b ± √ (b² - 4ac))

Joka vaadittiin näyttämään.

Erityistapaus

Joissain tapauksissa ratkaisua ongelmaan voidaan yksinkertaistaa. Joten parillisella kertoimella b saadaan yksinkertaisempi kaava.

Merkitse k = 1 / 2b, sitten kvadraattisen yhtälön juurten yleinen kaava on muoto:

x = (-k ± √ (k² - ac)) / a

D = 0: lle saadaan x = -k / a

Toinen erityistapaus on ratkaisu yhtälölle a = 1.

Näkymälle x² + bx + c = 0 juuret ovat x = -k ± √ (k² - c) jos erotin on suurempi kuin 0. Tapaukselle, kun D = 0, juuri määritetään yksinkertaisella kaavalla: x = -k.

Kaavioiden käyttö

Jokainen ihminen, edes epäilemättä sitä, on jatkuvasti edessään fyysisissä, kemiallisissa, biologisissa ja jopa sosiaalisissa ilmiöissä, jotka kuvataan hyvin kvadraattisella toiminnolla.

Huomaa: kvadraattisen funktion perusteella rakennettua käyrää kutsutaan parabooliksi.

Tässä muutamia esimerkkejä.

1. Laskettaessa ammuksen lentoreittiä käytetään liikkumisominaisuutta kehon paraboolia pitkin, joka vapautuu kulmassa horisontiin.
2. Parabolien ominaisuutta jakaa kuorma tasaisesti käytetään laajasti arkkitehtuurissa.

Ymmärtääksemme parabolisen funktion merkityksen, selvitämme kuinka tutkia sen ominaisuuksia kuvaajan avulla käsitteillä "erottava" ja "neliömäisen yhtälön juuret".

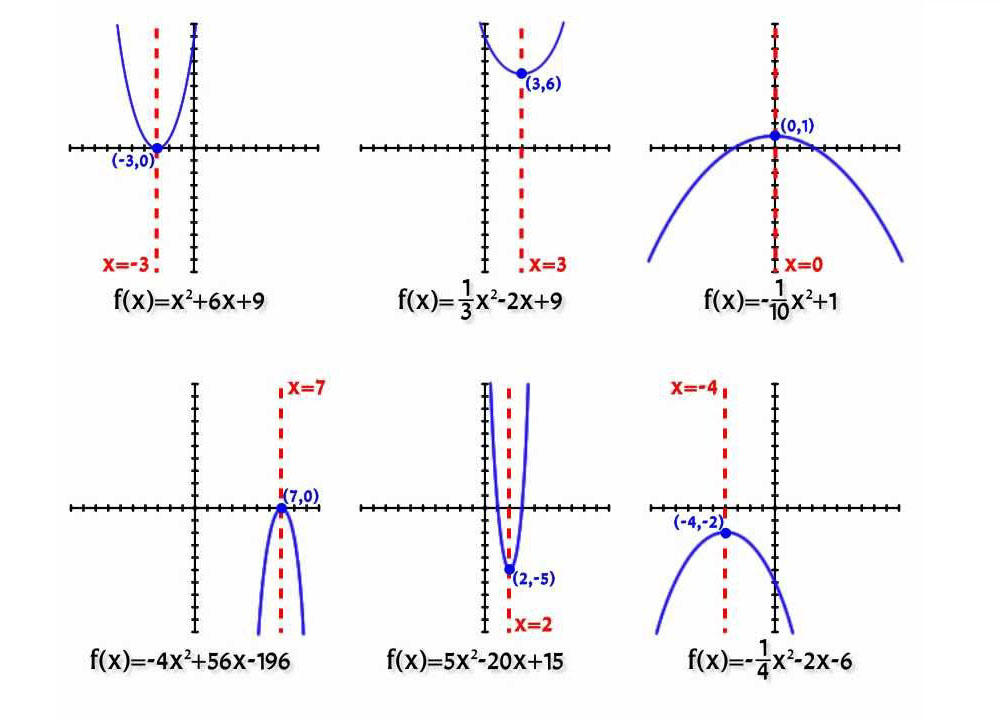
Kertoimien a ja b suuruudesta riippuen käyrän sijainnille on vain kuusi vaihtoehtoa:

1. Erottelija on positiivinen, a ja b ovat erilaisia ​​merkkejä. Parabolan haarat katsovat, kvadraattisessa yhtälössä on kaksi ratkaisua.
2. Erottava ja kerroin b ovat yhtä kuin nolla, kerroin a on suurempi kuin nolla. Kaavio sijaitsee positiivisella vyöhykkeellä, yhtälöllä on 1 juuri.
3. Erottelijalla ja kaikilla kertoimilla on positiiviset arvot. Neljännestä yhtälöllä ei ole ratkaisua.
4. Erottava ja kerroin a ovat negatiivisia, b on suurempi kuin nolla. Graafin haarat on suunnattu alaspäin, yhtälöllä on kaksi juuria.
5. Erotin ja kerroin b ovat yhtä kuin nolla, kerroin a on negatiivinen. Parabola näyttää alaspäin, yhtälöllä on yksi juuri.
6. Erottajan arvot ja kaikki kertoimet ovat negatiivisia. Ratkaisuja ei ole, funktion arvo on täysin negatiivisella alueella.

Huomaa: varianttia a = 0 ei oteta huomioon, koska tässä tapauksessa parabooli hajoaa suoraksi.

Kaikkia edellä esitettyjä kuvaa hyvin alla oleva kuva.

Esimerkkejä ongelmanratkaisusta

Ehto: käyttämällä yhteisiä ominaisuuksia, muodosta neliömäinen yhtälö, jonka juuret ovat keskenään yhtä suuret.

ratkaisu:

ongelman x ehdolla₁ = x₂tai -b + √ (b² - 4ac) / (2a) = -b + √ (b² - 4ac) / (2a). Yksinkertaista merkintää:

-b + √ (b² - 4ac) / (2a) - (-b - √ (b² - 4ac) / (2a)) = 0, avaa sulkeet ja anna samanlaiset ehdot. Yhtälö on muotoa 2√ (b² - 4ac) = 0. Tämä väite on totta, kun b² - 4ac = 0, joten b² = 4ac, sitten arvo b = 2√ (ac) korvataan yhtälöön

ah² + 2√ (ac) x + c = 0, pelkistetyssä muodossa saadaan x² + 2√ (c / a) x + c = 0.

vastaus:

jos a ei ole 0 ja mikä tahansa c, on vain yksi ratkaisu, jos b = 2√ (c / a).

Neliölliset yhtälöt kaikesta yksinkertaisuudestaanovat erittäin tärkeitä suunnittelulaskelmissa. Lähes mitä tahansa fyysistä prosessia voidaan kuvata jonkin verran likiarvolla käyttämällä järjestyksen n tehofunktioita. Neliöyhtälö on ensimmäinen tällainen likiarvo.