
Postoji nekoliko osnovnih algoritama za rješavanjezadaci sortiranja nizova. Jedna od najpoznatijih od njih je vrsta umetanja. Ova se metoda zbog svoje jasnoće i jednostavnosti, ali i male učinkovitosti koristi uglavnom u nastavi programiranja. Omogućuje vam razumijevanje osnovnih mehanizama sortiranja.
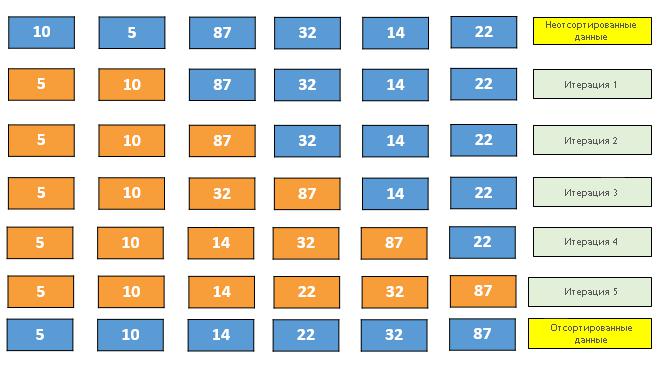
Suština algoritma za sortiranje umetanja ječinjenica da se unutar originalnog niza formira segment organiziran na željeni način. Svaki se element uspoređuje jedan s drugim s testiranim dijelom i ubacuje na svoje mjesto. Tako su nakon prolaska kroz sve elemente postrojeni u ispravnom redoslijedu.
Redoslijed odabira elemenata može biti bilo koji,mogu se odabrati proizvoljno ili prema nekom algoritmu. Najčešće se koristi sekvencijalno pretraživanje s početka polja, gdje se formira uređeni segment.
Početak sorte mogao bi izgledati ovako:
I tako sve do kraja izvornog niza.
Radi jasnoće, vrijedno je dati primjer kako se ovaj mehanizam sortiranja koristi u svakodnevnom životu.
Na primjer, uzmite novčanik. U odjeljku s novčanicama stotine, pet stotina i tisuću novčanica leže u neredu. Ovo je nered, u takvoj je gužvi teško odmah pronaći pravi komad papira. Niz računa se mora sortirati.
Prva je novčanica od 1000 rubalja, a odmah nakon nje - 100. Uzimamo stotinku i stavljamo je ispred. Treće u nizu je 500 rubalja, za nju je odgovarajuće mjesto između sto i tisuću.
Na isti način sortiramo dobivene karte prilikom igranja "Budala" kako bismo ih lakše kretali.

Način sortiranja umetanja uzima kao ulazizvorni niz koji se naređuje, funkcija usporedbe i, ako je potrebno, funkcija koja definira pravilo za nabrajanje elemenata. Najčešće se umjesto nje koristi operator regular petlje.
Prvi je element sam po sebi naručeni skup, pa usporedba počinje od drugog.
Algoritam često koristi pomoćnu funkciju za zamjenu dvije vrijednosti (swap). Koristi dodatnu privremenu varijablu, koja je intenzivna memorija i malo usporava kod.
Alternativa je kompenzacija grupne maseelemenata i naknadno umetanje sadašnjeg na ispražnjeni prostor. U ovom slučaju, prelazak na sljedeći element događa se kada je usporedba vratila pozitivan rezultat, što ukazuje na ispravan redoslijed.

Specifična implementacija uvelike ovisi o korištenom programskom jeziku, njegovoj sintaksi i strukturama.
Classic C implementacija pomoću privremene varijable za razmjenu vrijednosti:
int i, j, temp; za (i = 1; i <veličina; i ++) { temp = niz [i]; za (j = i - 1; j> = 0; j--) { if (niz [j] <temp) pauza; niz [j + 1] = niz [j]; niz [j] = temp; } }PHP implementacija:
funkcija insertion_sort (& $ a) { za ($ i = 1; $ i <count ($ a); $ i ++) { $ x = $ a [$ i]; za ($ j = $ i - 1; $ j> = 0 && $ a [$ j]> $ x; $ j--) { $ a [$ j + 1] = $ a [$ j]; } $ a [$ j + 1] = $ x; } }Ovdje se najprije svi elementi koji ne zadovoljavaju uvjet sortiranja pomaknu udesno, a zatim se trenutni element ubaci u oslobođeni prostor.
Java kod pomoću petlje:
javno statičko ubacivanje prazninaSort (int [] arr){ za (int i = 1; i <arr.length; i ++) { int currElem = arr [i]; int prevKey = i - 1; dok je (prevKey> = 0 && arr [prevKey]> currElem) { arr [prevKey + 1] = arr [prevKey]; arr [prevKey] = currElem; prevKey--; } } }Opće značenje koda ostaje nepromijenjeno: svaki element matrice se uzastopno uspoređuje s prethodnim i mijenja mjesta s njima ako je potrebno.
Očito, u najboljem slučaju, na ulazualgoritma će biti niz koji je već pravilno ispravljen. U ovoj situaciji algoritam će jednostavno morati provjeriti svaki element da bi se uvjerio da je na njegovom mjestu bez razmjene. Stoga će vrijeme izvođenja izravno ovisiti o duljini izvornog niza O (n).
U najgorem slučaju ulazni podaci su niz,sortirano obrnutim redoslijedom. Ovo će zahtijevati veliki broj permutacija, vrijeme izvođenja ovisit će o broju elemenata u kvadratu.
Točan broj permutacija za potpuno neuređeni niz može se izračunati pomoću formule:
n * (n-1) / 2, gdje je n duljina izvornog niza. Stoga je potrebno 4950 permutacija za postavljanje 100 elemenata u ispravnom redoslijedu.
Metoda umetanja vrlo je učinkovita za razvrstavanje malih ili djelomično uređenih nizova. Međutim, njegova se široka uporaba ne preporučuje zbog velike složenosti izračuna.
Algoritam se koristi kao pomoć u mnogim drugim složenijim metodama sortiranja.

Algoritam umetanja pripada tzvstabilne vrste. To znači da ne mijenja iste elemente, već zadržava njihov izvorni redoslijed. Indeks stabilnosti je često važan za pravilno naručivanje.

Iznad je sjajan vizualni primjer plesne vrste umetanja.


























