
Jelentős számú matematikai problémakapcsolatos az információterületen egyenetlenül eloszlott lelettel. A földrajzi helyzetű információs rendszerekről beszélünk, mivel ezekben lehetséges bizonyos pontokban megmérni a szükséges értékeket. Ezeknek a problémáknak a megoldására gyakran használnak egy vagy másik interpolációs módszert.

Az interpoláció egy számításaz értékek köztes értékei a rendelkezésre álló különálló értékkészlet szerint. A leggyakoribb interpolációs módszerek: az inverz súlyozott távolságok, a trend felület és a kriging módszer.
Tehát nézzük közelebb az első módszert, annak lényegéta becsült pontokhoz közeli pontok befolyásolásából áll, összehasonlítva a további pontokkal. Egy ilyen interpolációs módszer használatakor meg kell választani egy bizonyos környéken egy adott topográfia közül azt a pontot, amely a legnagyobb hatással van rá. Ez kiválasztja a maximális keresési sugarat vagy az adott ponthoz közeli pontok számát. Ezután az egyes pontokban beállítják a súlyt a magasságra, az e ponttól való távolságtól függően. Csak így lehet elérni a legközelebbi pontok nagyobb mértékű hozzájárulását az interpolált magassághoz, ha összehasonlítunk egy adott ponttól nagyobb távolságban lévő pontokkal.
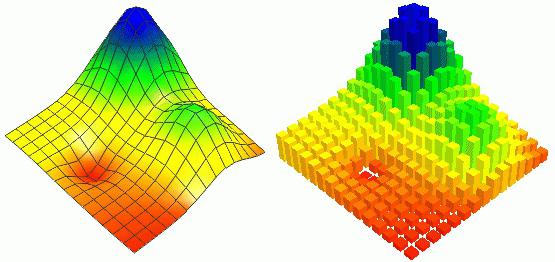

Van egy másik meghatározási eszközkonkrét pontok - a kvadratikus interpoláció módszere, amelynek lényege, hogy egy bizonyos intervallumon belüli funkciót helyettesítsen egy kvadratikus parabolával. Ráadásul annak végtagját analitikusan számítják ki. A hozzávetőleges (minimális vagy maximális) helyét követően be kell állítani egy bizonyos értéktartományt, amely után a megoldás keresése folytatódhat. Az eljárás ismételt megismétlése az iteratív eljárás alkalmazásával finomítja az egyenlet értékét az eredményhez a probléma megállapításában megadott pontossággal.


























