
平面上にさまざまな形状を正しく表示する機能 シート、キャンバス、その他の表面はかなり重要なスキル。そしてまず第一に、それは芸術家:画家、彫刻家、グラフィックアーティスト、デザイナー(建物の内部空間と建築環境)、そして科学者:数学者、物理学者、デザイナー、発明者の両方にとって重要です。
しかし、これらの領域から遠く離れた人も学ぶことができます私たちの周りの世界を正しく認識して表示することも重要です。これは、そのすべての多様性をより深く理解するのに役立ちます。これを正しく行う方法について十分なアイデアがない場合は、プロジェクト、写真、または発明の図面が成功しない可能性があります。つまり、このスキルは、単純な日常のタスクを解決するためにも、グローバルで普遍的に重要なタスクを解決するためにも重要です。
古くから人々は何かを描写しようとしてきました彼らが彼らの周りで見たもの:他の人々、当時のいくつかの原始的な建物、動植物の驚くほど美しい世界、雄大な山々、そしてただのもの、家庭用品。つまり、その多様性と壮大さのすべての世界。
しかし、それでも彼らはそれがどうだったかわからなかった正確かつ有能に実行することが可能であるため、平面上のさまざまな体積オブジェクトの表示は、実にリアルで生き生きとしています。その人は適切な知識を持っていませんでした、そしてさらにそれ以上に、おそらく最も基本的なものを数えずに、特別なスキルはありませんでした。
以前の情報源では、世界で最初の絵は、人の影に沿って走る一本の線だけで構成され、壁に太陽が投げかけました。つまり、自然自体が、この問題の正しい解決策を探すためにどちらの方向に進むかを促しています。
そして、この質問は当時の男さえも心配していましたそしてこの理由から、彼は、いわばオリジナルのボリュームのある生きたシルエットを単に賞賛したくはありませんでしたが、平面上の空間オブジェクトをキャプチャしようとしました。そして、彼はこのように彼の家や彼のための神聖な場所を飾ることができるように、または彼と一緒に写真と一緒に束を取り、それを任意の距離に移動できるようにするためにこれを行いました。
そして、あなたが言うことは何でも、何年も経ち、何世紀も経ちましたそしてどういうわけか、文明が発展するにつれて、人々は徐々に複雑な図を二次元空間、つまり平面に表示することを学びました。描かれたオブジェクトの寸法と比率の精度が非常に近似しているように見え始めたのは今だけです。
しかし、問題は表示がどれほど正しいかということです平面上の数字とそれらが体積の初期オブジェクトにどれだけ対応するかは、かつて非常に関連性がありました。ある意味で、幾何学と呼ばれる新しい科学がこの問題の解決に役立ちました。むしろ、そのセクションは画法幾何学です。
ここで彼女は、3次元空間と2次元空間の両方で、図形と平面、線と点、およびそれらの相互関係を研究しているだけです。
視覚芸術の重要な特徴画像平面上の図の表示です。結局のところ、実際には、それは2次元の3次元空間オブジェクトのキャプチャです。つまり、複合体は単純に変換する必要があります。つまり、長さ、幅、高さを持つオブジェクトを平面に変換する必要があります。
そして、いくつかの方法のおかげで、記述幾何学はそのような「遷移」を行います。それらの約6つがあります。これが3つの主要なものであり、世界中で最も人気があります:
描かれたオブジェクトは非常にはっきりと見えます軸測投影法(直交および斜めを含む)。しかし、遠近法で描写すると、最も明確かつ真に投影されます。そして、平面上に図を表示する方法の問題を大部分解決するのは上記の方法です。

他のイメージの方法の中での視点最も名誉ある場所を取ります。なぜなら、人間の目はカメラのレンズと同じように周囲の空間を同じように見ているからです。観察者から遠いものはサイズが小さく見え、近くにある場合よりもはるかに小さい場合があります。
たとえば、宇宙の立方体の画像を撮りましょう。実際、すべてのエッジが互いに平行である場合、このオブジェクトを遠くから見ると、エッジが1点で収束している(または収束しているはずである)ように見える場合があります。そして、最も興味深いのは、それらは1つの点に収束する必要があるだけでなく、単一の交点を持っていることです。
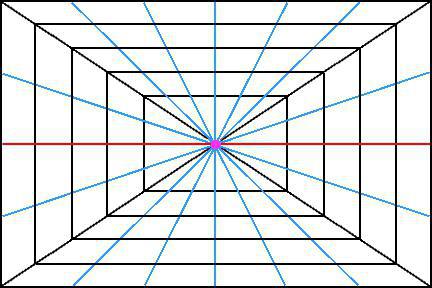
ルネッサンスの巨匠に感謝します:アルブレヒト・デューラー、ピエロ・デラ・フランチェスカ、アンドレア・マンテーニャ、レオン・バッティスタ・アルベルティ、現代絵画は、直接線形遠近法とは何か、地平線の高さと消失点を決定する方法を知っています。
そして世界的に有名な天才-レオナルドダヴィンチ-最初に空気遠近法の概念について議論しました。これは、オブジェクトの色、色調、コントラスト特性の変化です(オブジェクトが削除されると減少します)。

直交とは平行を指します平面に垂直な直線に向けられたデザイン。その適用の過程で、オブジェクトの輪郭の寸法は変更されません。つまり、オブジェクトは歪みなく表示されます。
投影された3次元オブジェクト、いわば側面、正面、上面の3つのビューに分解されます。そして、これらすべてを同時に見ると、オブジェクトがボリュームでどのように見えるかについてのアイデアを追加することができます。同時に、図の寸法は3D画像と2D画像の両方で変更されません。

この予測は、さらにいくつかの亜種に細分されます。
すべてで等角歪みを行う3軸(長さ、幅、高さ)。つまり、ペアの軸間の角度は120度に等しくなります。ダイメトリックの場合、2つの軸に沿った歪みは等しく、3番目の軸は異なります。また、トリメトリック投影では、すべての歪み係数(つまり、3つの軸すべてに沿った)が異なります。
軸に沿って直角三角形を回転させる場合2本の脚のうちの1本のうち、3番目の辺(斜辺)は円錐と呼ばれる新しい図形を表します。そして、その辺の1つに沿って長方形(正方形)を回転させると、円柱になります。半円が回転すると球が出てきます。
したがって、ある軸に沿って平面を回転させることにより、いわゆる回転図が得られます。

これらの図には回転軸があります。それらが平面にどのように表示されるかは、目の高さに対するそれらの配置によって異なります。たとえば、円柱の上面と下面は基本的に円です。そして、それらを平面で見ると、楕円のように見えます。
しかし、次の場合、タスクはさらに困難になります平面上に空間図を表示し、それらは傾斜した軸を持っています。この場合、回転体の輪郭が回転体の軸から等距離にあることが重要です。
平面上に形状を表示する場合に不可欠キアロスクーロを再生します。描かれたオブジェクトの体積は、線だけでなく、その側面の光と影の正しい分布によっても作成されるためです。そして、それは二次元の表面の平面でかなりボリュームがあるように見えます。

したがって、平面上の図の表示は、それらのサイズの決定、特に明度と暗点の正しい面付けは、上記の方法のおかげで実行することがかなり可能です。そして、最も重要なことは、これらは私たちの時代の主要な専門家によって使用されているすでに本当に証明された方法です。
