
기하학은 매우다면적인 과학입니다. 그녀는 논리, 상상력 및 지능을 개발합니다. 물론 복잡성과 엄청난 수의 정리와 공리로 인해 학생들은 항상 그것을 좋아하지는 않습니다. 또한 일반적으로 인정되는 표준 및 규칙을 사용하여 결론을 지속적으로 증명해야합니다.

모서리 형성
두 각도의 교차로 모든 각도가 형성됩니다.한 지점에서 두 개의 광선을 직접 또는 유지합니다. 그것들은 한 글자 또는 세 글자로 불릴 수 있으며, 각도의 구성 지점을 연속적으로 나타냅니다.
Углы измеряются в градусах и могут (в зависимости 그들의 의미에서) 다르게 호출됩니다. 따라서 직각, 날카 롭고 무딘 배치가 있습니다. 각 이름은 특정 정도 측정 또는 해당 간격에 해당합니다.
둔각은 90도 이상입니다.
각도 측정 값이 90 일 때 각도를 직각이라고합니다.
하나의 실선으로 구성되어 있고 각도가 180 도인 경우를 확장이라고합니다.
인접한 코너
공통 측면, 두 번째 측면이있는 모서리서로 계속되는 것을 인접이라고합니다. 날카 롭거나 뭉툭 할 수 있습니다. 평평한 모서리가 선으로 교차하면 인접한 모서리가 형성됩니다. 그 속성은 다음과 같습니다.
이러한 속성 덕분에 다른 각도의 값 또는 적어도 그 사이의 비율을 갖는 각도의 각도 측정을 항상 계산할 수 있습니다.

변이 서로 연속되는 각도를 수직이라고합니다. 그들의 품종은 모두 그러한 쌍으로 작용할 수 있습니다. 수직 각도는 항상 서로 동일합니다.
직선이 교차 할 때 형성됩니다. 인접한 모서리는 항상 함께 표시됩니다. 각도는 동시에 인접하고 다른 각도에 수직 일 수 있습니다.
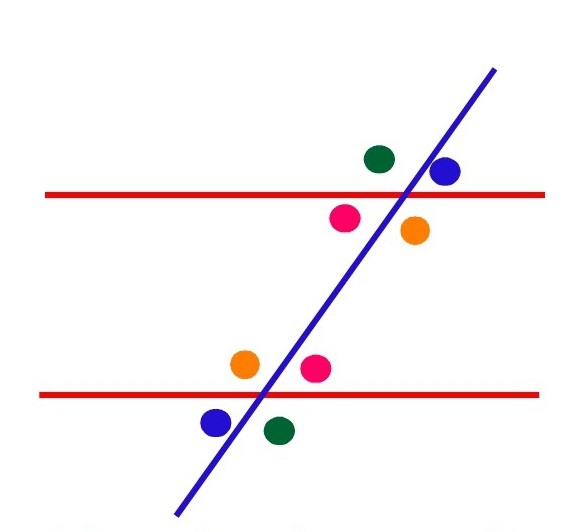
임의의 평행선 교차점에서다른 여러 유형의 각도도 선으로 고려됩니다. 이러한 선을 시컨트 (secant)라고하며 해당하는 일면 및 교차 각도를 형성합니다. 그들은 서로 동일합니다. 수 직각과 인접 각이 갖는 특성을 고려하여 볼 수 있습니다.
따라서 각도의 주제는 상당히간단하고 간단합니다. 모든 속성은 기억하고 증명하기 쉽습니다. 각도가 숫자 값에 해당하는 한 문제를 해결하는 것은 어렵지 않습니다. 이미 더 나아가 죄와 죄에 대한 연구가 시작되면 많은 복잡한 공식, 결론 및 결과를 외워야 할 것입니다. 그때까지는 인접한 모서리를 찾아야하는 쉬운 작업을 즐길 수 있습니다.
