
Mokymasis mokykloje sprendžiant lygtis klasėjematematikų, daugelis studentų dažnai būna tikri, kad eikvoja laiką, ir vis dėlto toks įgūdis yra naudingas gyvenime ne tik tiems, kurie nusprendžia sekti Dekarto, Eulerio ar Lobačiovskio pėdomis.
Praktiškai, pavyzdžiui, medicinoje ar ekonomikoje,gana dažnai būna situacijų, kai specialistui reikia išsiaiškinti, kada tam tikro vaisto veikliosios medžiagos koncentracija paciento kraujyje pasiekia reikiamą lygį arba jei reikia apskaičiuoti laiką, reikalingą tam tikram verslui, kad jis taptų pelningas.
Dažniausiai tai yra netiesinis sprendimasįvairių tipų lygtys. Norėdami tai padaryti kuo greičiau, ypač naudojant kompiuterius, naudokite skaitinius metodus. Jie yra gerai ištirti ir jau seniai įrodyti, kad yra veiksmingi. Tarp jų yra Niutono liestinės metodas, kuriam skirtas šis straipsnis.

Šiuo atveju yra funkcija g, kuri yra suteikiama intervale (a, b) ir užima tam tikras reikšmes, tai yra, kiekvienam x, priklausančiam (a, b), galima susieti tam tikrą skaičių g (x).
Reikalaujama nustatyti visas lygties šaknis iš intervalo tarp taškų a ir b (įskaitant galus), kurių funkcija nulio. Akivaizdu, kad tai bus y = g (x) ir OX sankirtos taškai.
Kai kuriais atvejais patogiau g (x) = 0 pakeisti panašia g formos forma1(x) = g2(x). Šiuo atveju šaknys yra grafikų g susikirtimo taškų abscisės (x reikšmė)1(x) ir g2(x).
Problemoms taip pat svarbu išspręsti netiesinę lygtįoptimizacijos, kurioms esant vietinio ekstremumo sąlyga yra ta, kad funkcijos darinys išnyksta. Kitaip tariant, tokią problemą galima sumažinti ieškant lygties p (x) = 0 šaknų, kur p (x) yra identiškas g "(x).
Kai kuriems netiesinių lygčių tipams,pavyzdžiui, kvadratinės arba paprastos trigonometrinės, šaknis galite rasti gana paprastais būdais. Visų pirma, kiekvienas studentas žino formules, kuriomis naudodamiesi galite lengvai rasti argumentų reikšmes taškuose, kur kvadratinė trinomė lygi nuliui.
Netiesinių lygčių šaknų ištraukimo metodaiĮprasta skirstyti į analitinius (tiesioginius) ir kartojamuosius. Pirmuoju atveju norimas sprendimas yra formulės formos, pagal kurią atliekant daugybę aritmetinių operacijų galima rasti norimų šaknų vertę. Panašūs metodai yra sukurti eksponentinėms, trigonometrinėms, logaritminėms ir paprasčiausioms algebrinėms lygtims. Likusioms dalims reikia naudoti specialius skaitmeninius metodus. Juos lengva įgyvendinti naudojant kompiuterius, kurie leidžia reikiamu tikslumu rasti šaknis.
Tarp jų yra vadinamasis liestinių skaitinis metodas. Pastarąjį pasiūlė didysis mokslininkas Isaacas Newtonas XVII amžiaus pabaigoje. Vėlesniais amžiais metodas buvo ne kartą tobulinamas.
Skaitmeniniai metodai sprendžiant sudėtingas lygtis, o neturint analitinius sprendimus, priimtina atlikti du etapus. Pirmiausia turite juos lokalizuoti. Ši operacija susideda iš tokių segmentų radimo OX, kuriuose yra viena sprendžiamos lygties šaknis.
Apsvarstykite segmentą [a, b].Jei g (x) neturi pertraukimų, o taškuose yra priešingų ženklų reikšmės, tada tarp a ir b arba juose yra bent 1 lygties g (x) = 0 šaknis. būti unikalus, reikalaujama, kad g (x) ant [a, b] būtų monotoniškas. Kaip žinote, jis turės šią savybę, jei g '(x) yra pastovus ženklas.
Kitaip tariant, jei ant [a, b] g (x) neturi pertraukimų ir monotoniškai didėja arba mažėja, o jo reikšmės galiniuose taškuose turi skirtingus ženklus, tada [a, b] yra 1 ir tik 1 šaknis g (x).
Tuo pačiu metu turėtumėte žinoti, kad šis kriterijus netaikomas daugybinių lygčių šaknims.
Prieš svarstant sudėtingesnius skaitinius metodus (liestinės metodas ir jo atmainas) verta susipažintilengviausias būdas nustatyti šaknis. Jis vadinamas dichotomija ir nurodo intuityvius metodus. Šaknų radimo algoritmas pagrįstas teorema, kad jei g (x) yra nepertraukiamas [x0, x1] skirtingų ženklų sąlyga yra tenkinama, tada laikomasi intervalo yra bent 1 šaknis g (x) = 0.
Norėdami jį rasti, turite padalyti segmentą [x0, x1] per pusę ir pažymėkite vidurio tašką kaip x2... Tada galimi du variantai: g (x0) * g (x2) arba g (x2) * g (x1) yra lygūs arba mažesni už 0. Pasirinkite tą, kuriam tinka viena iš šių nelygybių. Mes kartojame aukščiau aprašytą procedūrą, kol ilgis [x0, x1] netaps mažesne už tam tikrą iš anksto pasirinktą vertę, kuri lemia lygties šaknies nustatymo tikslumą [x0, x1tu
Metodo privalumai yra jo patikimumas irpaprastumas, o trūkumas yra būtinybė iš pradžių nustatyti taškus, kuriuose g (x) užima skirtingus ženklus, todėl jo negalima naudoti šaknims, turinčioms net daugybę. Be to, jis nėra apibendrintas lygčių sistemos atveju arba kai kalbama apie sudėtingas šaknis.
Tarkime, kad norime išspręsti lygtį g (x) = 2x5 + x - 1 = 0.Kad ilgai neieškotume tinkamo segmento, mes sukuriame grafiką naudodami, pavyzdžiui, gerai žinomą programą „Excel“. Matome, kad šaknies lokalizavimui geriau kaip reikšmes imti intervalą [0,1]. Galime būti tikri, kad jis turi bent vieną norimos lygties šaknį.
g "(x) = 10x4 + 1, tai yra monotoniškai didėjanti funkcija, todėl pasirinktame segmente yra tik 1 šaknis.
Pakeiskite taškus į lygtį.Mes turime atitinkamai 0 ir 1. Pirmajame žingsnyje sprendimu laikome 0,5 tašką. Tada g (0,5) = -0,4375. Tai reiškia, kad kitas segmentas, padalytas į pusę, bus [0,5, 1]. Jo vidurio taškas yra 0,75. Funkcijos vertė joje yra 0,226. Atsižvelgiame į segmentą [0,5, 0,75] ir jo vidurį, esantį taške 0,625. Įvertinkite g (x) reikšmę 0,625. Ji lygi -0,11, o tai yra neigiama. Pagal šį rezultatą pasirinkite segmentą [0,625, 0,75]. Gauname x = 0,6875. Tada g (x) = -0,00532. Jei sprendimo tikslumas yra 0,01, tada galime manyti, kad norimas rezultatas yra 0,6875.
Šis šaknų paieškos metodas naudojant Newtono tangentinį metodą yra populiarus dėl labai greito suartėjimo.
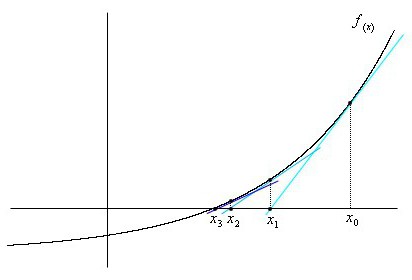
Jis pagrįstas įrodytu faktu, kad jei xP. - priartinimas prie šaknies f (x) = 0, kad f "C1, tada kitas aproksimavimas bus tame taške, kur nulinės liestinės ir f (x) lygtis, t.

Pakeiskite x = xn + 1 ir nustatykite y nulį.
Tada liestinio metodo algoritmas atrodo taip:

Pabandykime naudoti klasikinį Niutono tangentinį metodą ir rasti netiesinės lygties sprendimą, kurį analitiškai rasti sunku arba neįmanoma.
Tebūna reikalaujama nustatyti x šaknis3 Pavyzdžiui, + 4x - 3 = 0 tam tikru tikslumu0,001. Kaip žinote, bet kurios funkcijos nelyginio laipsnio polinomo pavidalo grafikas turi bent kartą kirsti OX ašį, tai yra, nereikia abejoti šaknų egzistavimu.
Prieš spręsdami savo pavyzdį naudodami liestinės metodą, mes sukuriame grafiką f (x) = x3 + 4x - 3 taškų. Tai labai lengva padaryti, pavyzdžiui, naudojant „Excel“ skaičiuoklę. Iš gauto grafiko bus matyti, kad [0,1] jis kerta OX ašį ir funkciją y = x3 + 4x - 3 padidėja monotoniškai. Mes galime būti tikri, kad [0,1] lygybėse x3 + 4x - 3 = 0 turi sprendimą ir jis yra vienintelis.
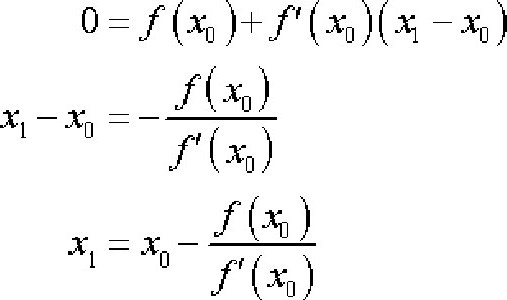
Bet koks lygčių sprendimas liestinės metodu pradedamas skaičiuojant f "(x). Turime:
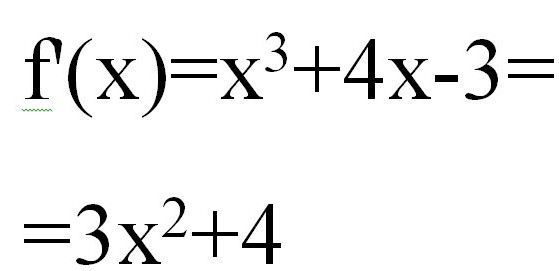
Tada antrasis darinys bus formos x * 6.
Naudodami šias išraiškas, mes galime parašyti formulę, leidžiančią nustatyti lygties šaknis, naudojant formos liestinės metodą:

Tada turite pasirinkti pradinį apytikslį dydį, ty spręsti, kurį tašką atsižvelgti į pradinį tašką (ob.x0) iteraciniam procesui. Apsvarstykite segmento galus [0,1]. Mums tinka tas, kuriam funkcijos sąlyga ir antrasis jos išvestinis x0... Kaip matote, pakeisdami x0 = 0 tai pažeista, bet x0 = 1 yra gerai.
Nes

tada, jei mus domina sprendimas liestinių metodu, kurio tikslumas e, tada reikšmė xP. gali būti laikoma tenkinančia problemos reikalavimus, jei nelygybė | f (xP.) / f ’(xP.) | <e.
Pirmame problemos sprendimo tangentiniu metodu žingsnyje turime:

Ankstesnį pavyzdį galima išspręsti daug lengviau ir greičiau, jei neatliekate skaičiavimų rankiniu būdu (naudodamiesi skaičiuokle), bet naudojate „Microsoft“ skaičiuoklės procesoriaus galimybes.
Norėdami tai padaryti, programoje „Excel“ turite sukurti naują puslapį ir užpildyti jo langelius šiomis formulėmis:
Tada pirmiausia turite „ištempti“ C, D ir E stulpelių formules dviem eilutėmis, o po to, kai jose pasirodys vertės, atlikite tą patį su B stulpeliu.
Konkrečioje užduotyje jau bus rodoma langelyje B10užrašas „Iteracijų užbaigimas“, o problemai išspręsti reikės paimti skaičių, įrašytą langelyje, esančiame viena eilute aukščiau. Tam galite pasirinkti atskirą „išplečiamąjį“ stulpelį, įvesdami ten sąlyginę formulę, pagal kurią rezultatas bus parašytas ten, jei turinys viename ar kitame B stulpelio langelyje bus „Kartojimų užbaigimas“.
Pabandykime gauti netiesinės lygties y = x sprendimą4 - 4 - 2 * x pagal tangentinį metodą Paskalyje.
Mes naudojame tokią pagalbininko funkcijąpadės apytiksliai apskaičiuoti f "(x) = (f (x + delta) - f (x)) / delta. Kaip iteracinio proceso užbaigimo sąlygą pasirenkame nelygybės | x įvykdymą0-x1| <kažkoks nedidelis skaičius. Paskalyje tai rašome kaip abs (x0 - x1) <= epsilonas.
Programa yra nuostabi tuo, kad jai nereikia rankiniu būdu apskaičiuoti išvestinės priemonės.

Apsvarstykite kitą būdą nustatyti šaknisnetiesinės lygtys. Kartojimo procesas susideda iš to, kad kaip nuoseklūs artėjimai prie norimo šaknies f (x) = 0, imamos akordo susikirtimo taškų su galinių taškų a ir b abscesais su OX taškų vertės , žymimas kaip x1, ..., xP. ... Mes turime:
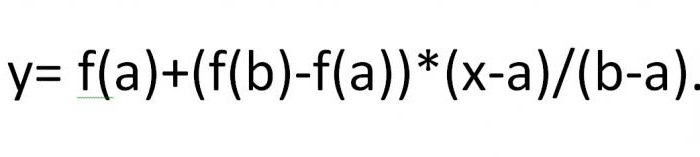
Taškui, kuriame akordas kerta OX ašį, išraiška bus parašyta taip:

Tegul antrasis išvestinis yra teigiamas x £ [a, b] (priešingas atvejis bus sumažintas iki nagrinėjamo, jei parašysime - f (x) = 0). Šiuo atveju grafikas y = f (x) yra kreivė, išgaubta apačioje ir esanti po akordu AB... Gali būti 2 atvejai: kai funkcijos taške a teigiama reikšmė arba b taške ji yra neigiama.
Pirmuoju atveju mes pasirenkame galą a kaip fiksuotą ir x0 imkitės b punkto. Tada vienas po kito einantys apytiksliai apskaičiavimai pagal anksčiau pateiktą formulę sudaro seką, kuri monotoniškai mažėja.
Antruoju atveju galinis taškas b yra fiksuotas ties x0 = a. Kiekviename iteracijos etape gautos x vertės sudaro monotoniškai didėjančią seką.
Taigi galime teigti, kad:
Kartojimai gali būti tęsiami tol, kol bus įvykdytos šaknų artumo sąlygos šiame ir ankstesniame kartojimo etape modulo abs (xm - xm - 1) <e.
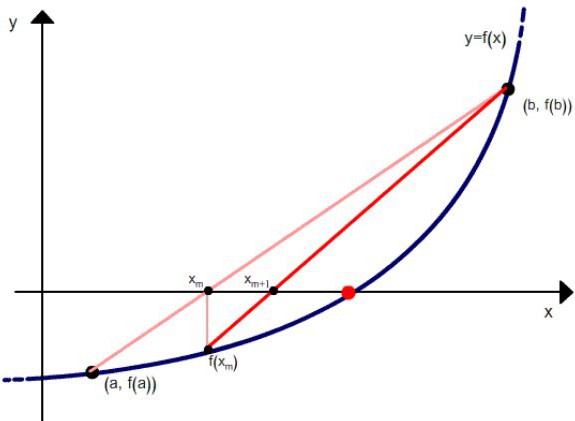
Kombinuotas akordų ir liestinių metodas leidžia nustatyti lygties šaknis,artėja prie jų iš skirtingų pusių. Tokia vertė, prie kurios grafikas f (x) kerta OX, leidžia patobulinti tirpalą daug greičiau nei kiekvienam iš metodų atskirai.
Tarkime, kad jums reikia rasti šaknis f (x) = 0, jeijie yra ant [a, b]. Galite taikyti bet kurį iš aukščiau aprašytų metodų. Tačiau geriausia išbandyti jų derinį, kuris labai padidins šaknies tikslumą.
Apsvarstykite atvejį su pradiniu aproksimavimu, atitinkančiu sąlygą, kad pirmasis ir antrasis išvestiniai turi skirtingus ženklus tam tikrame taške x.
Tokiomis sąlygomis netiesinių lygčių sprendimas tangentiniu metodu leidžia rasti šaknį su pertekliumi, jei x0= b, o metodas, naudojant akordus su fiksuotu galu b, leidžia rasti apytikslę šaknį su trūkumu.
Naudojamos formulės:

Dabar reikia ieškoti reikalingos šaknies x intervale [a1, gim1]. Kitas žingsnis - taikyti kombinuotą metodą šiam segmentui. Veikdami taip, mes gauname formos formules:

Jei įvyksta pirmojo ir antrojo darinių ženklų skirtumas, tada, ginčydamiesi panašiai, norėdami patikslinti šaknį, gauname šias rekursines formules:

Įvertinta nelygybė bP.+1 - aP.+1| <e. Kitaip tariant, praktiškai jūs turite rasti sprendimą naudodamiesi dviem metodais, tačiau kiekviename žingsnyje turite išsiaiškinti, kiek rezultatai yra arti vienas kito.
Jei minėta nelygybė yra teisinga, tadakaip netiesinės lygmens tam tikrame segmente šaknis, mes paimame tašką, kuris yra tiksliai viduryje tarp sprendimų, rastų tam tikrame iteracijos etape.
Kombinuotas metodas yra lengvai įgyvendinamas TURBO PASCAL aplinkoje. Jei norite, galite pabandyti atlikti visus skaičiavimus lentelės metodu „Excel“ programoje.
Pastaruoju atveju, norint išspręsti problemą naudojant akordus, parenkami keli stulpeliai ir atskirai - Isaaco Newtono siūlomas metodas.
Be to, kiekviena eilutė naudojama rašytiskaičiavimai konkrečiu iteracijos žingsniu dviem metodais. Tada, kairėje nuo sprendimo srities, aktyviame darbo puslapyje paryškinamas stulpelis, kuriame įrašomas kiekvieno iš metodų kito iteracinio žingsnio reikšmių skirtumo modulio apskaičiavimo rezultatas. Kitas gali būti naudojamas skaičiavimo rezultatams įvesti pagal formulę, pagal kurią apskaičiuojama loginė struktūra „IF“, kuri naudojama norint sužinoti, ar sąlyga įvykdyta, ar ne.
Dabar jūs žinote, kaip išspręsti sudėtingas lygtis. Liestinės metodas, kaip jau matėte, ją įgyvendinti „Pascal“ ir „Excel“ yra gana paprasta. Todėl naudodami formules visada galite nustatyti lygties, kurią sunku ar neįmanoma išspręsti, šaknis.


























