
В начале 19 века геометр из Берлина Якоб Штейнер Postanowił połączyć trzy wioski tak, aby ich długość była jak najkrótsza. Następnie uogólniał ten problem: konieczne jest znalezienie punktu na płaszczyźnie, tak aby odległość od niego do n innych punktów była najmniejsza. W XX wieku kontynuowano prace na ten temat. Zdecydowano wziąć kilka punktów i połączyć je tak, aby odległość między nimi była jak najkrótsza. To wszystko jest szczególnym przypadkiem badanego problemu.
Algorytm Kruskala odnosi się do chciwości(nazywane są również gradientem). Ich istotą jest największy zysk na każdym kroku. Nie zawsze „chciwe” algorytmy dają najlepsze rozwiązanie problemu. Istnieje teoria pokazująca, że zastosowane do niektórych zadań zapewniają optymalne rozwiązanie. To jest teoria matroidów. Algorytm Kraskala odnosi się do takich problemów.
Рассматриваемый алгоритм строит оптимальный rama wykresu. Problem jest następujący. Nieukierowany wykres jest podawany bez wielu krawędzi i pętli, a funkcja wagi w jest podana na zbiorze jego krawędzi, który przypisuje każdej krawędzi e liczbę - ciężar krawędzi - w (e). Ciężar każdego podzbioru zestawu krawędzi jest określany przez sumę wag jego krawędzi. Konieczne jest znalezienie ramy o najmniejszej masie.
Algorytm Kruskala działa w ten sposób.Po pierwsze, wszystkie krawędzie oryginalnego wykresu są ułożone w porządku rosnącym wag. Początkowo szkielet nie zawiera żadnych krawędzi, ale obejmuje wszystkie wierzchołki grafu. Po kolejnym kroku algorytmu do już zbudowanej części szkieletu, która jest lasem spinającym, dodawana jest jedna krawędź. Nie jest wybierany arbitralnie. Wszystkie krawędzie grafu, które nie należą do modelu szkieletowego, można nazwać czerwonymi i zielonymi. Wierzchołki każdej czerwonej krawędzi znajdują się w tym samym komponencie łączności budowanego lasu, a wierzchołki zielonej krawędzi znajdują się w różnych. Dlatego jeśli dodasz tam czerwoną krawędź, pojawi się cykl, a jeśli będzie zielona, składnik łączności w lesie uzyskany po tym kroku będzie o jeden mniej. Tak więc do powstałej konstrukcji nie można dodać czerwonej krawędzi, ale można dodać dowolną zieloną krawędź, aby stworzyć las. I dodaje się zielona krawędź o minimalnej wadze. Rezultatem jest najlżejsza rama.
Oznaczmy obecny las F.Dzieli zbiór wierzchołków grafu na obszary łączności (ich suma form F i nie przecinają się parami). Czerwone krawędzie mają oba wierzchołki w tej samej części. Część (x) to funkcja, która dla każdego wierzchołka x zwraca nazwę części, do której należy x. Unite (x, y) to procedura, która buduje nową partycję, składającą się z połączenia części x i y oraz wszystkich innych części. Niech n będzie liczbą krawędzi w grafie. Wszystkie te pojęcia są zawarte w algorytmie Kruskala. Realizacja:
Uporządkuj wszystkie krawędzie wykresu od 1-go do n-tego w porządku rosnącym wag. (ai, bi to wierzchołki krawędzi o numerze i).
dla i = 1 do n zrobić.
x: = Część (ai).
y: = Część (bi).
Jeśli x nie jest równe y, to Zjednocz (x, y), uwzględnij krawędź i w F.
Niech T będzie szkieletem oryginalnego grafu skonstruowanego algorytmem Kruskala, a S jego dowolnym szkieletem. Musimy udowodnić, że w (T) nie przekracza w (S).
Niech M będzie zbiorem krawędzi S, P będzie zbiorem krawędziT. Jeśli S nie jest równe T, to istnieje krawędź et układu T, która nie należy do S. Łączmy et z S. Powstaje cykl, nazwijmy go C. Usuwamy z C dowolną krawędź es należące do S. Otrzymujemy nową ramkę, bo krawędzie i tyle jest w niej szczytów. Jego waga nie przekracza w (S), ponieważ w (et) jest co najwyżej w (es) na mocy algorytmu Kruskala. Tę operację będziemy powtarzać (zastępując krawędzie S krawędziami T) aż otrzymamy T. Waga każdej kolejnej wynikowej klatki nie jest większa od wagi poprzedniej, z czego wynika, że w (T) nie jest większe niż w (S).
Również poprawność algorytmu Kruskala wynika z twierdzenia Rado-Edmondsa o matroidach.
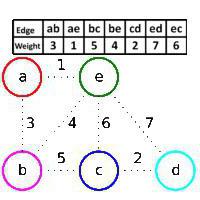
Mając graf z wierzchołkami a, b, c, d, e i krawędziami (a,b), (a, e), (b, c), (b, e), (c, d), (c, e), (d, e). Masy żeber podane są w tabeli i na rysunku. Początkowo budowany las F zawiera wszystkie wierzchołki grafu i nie zawiera żadnych krawędzi. Algorytm Kruskala najpierw dodaje krawędź (a, e), ponieważ ma najmniejszą wagę, a wierzchołki a i e znajdują się w różnych połączonych składowych lasu F (krawędź (a, e) jest zielona), potem krawędź ( c, d), a zatem, że ta krawędź ma najmniejszą wagę z krawędzi grafu, które nie należą do F i jest zielona, to z tych samych powodów dodaje się krawędź (a, b). Ale krawędź (b, e) jest pomijana, mimo że ma najmniejszą wagę z pozostałych krawędzi, ponieważ jest czerwona: wierzchołki b i e należą do tej samej połączonej składowej lasu F, czyli jeśli dodamy krawędź (b, e) do F, otrzymujemy cykl. Następnie dodawana jest zielona krawędź (b, c), czerwona krawędź (c, e) jest pomijana, a następnie d, e. Zatem krawędzie (a, e), (c, d), (a, b), (b, c) są dodawane sekwencyjnie. Z nich składa się optymalny szkielet początkowego grafu. Tak działa algorytm w tym przypadku Namalowany. Pokazuje to przykład.

Rysunek przedstawia wykres składający się z dwóch połączonych elementów. Pogrubione linie pokazują krawędzie optymalnego modelu krawędziowego (zielonego) skonstruowanego za pomocą algorytmu Kruskala.

Górny rysunek przedstawia oryginalny wykres, a dolny przedstawia ramy minimalnej wagi skonstruowane dla niego przy użyciu rozważanego algorytmu.
Kolejność dodanych krawędzi: (1,6); (0,3), (2,6) lub (2,6), (0,3) - nie ma znaczenia; (3.4); (0,1), (1,6) lub (1,6), (0,1) jest również obojętne (5,6).

Algorytm Kruskala znajduje praktyczne zastosowanie, np. do optymalizacji układania komunikacji, dróg w nowych dzielnicach osiedli każdego kraju, a także w innych przypadkach.


























